


Funzione zeta di Riemann
In matematica,
mostrò che vi è una relazione tra gli zeri della funzione e la distribuzione dei numeri primi osservando che una congettura sulla posizione degli zeri (la celebre Ipotesi di Riemann) implicherebbe che i primi sono distribuiti con una certa regolarità.
Storia
Bernhard Riemann fu il primo ad evidenziare
la connessione tra gli zeri della funzione zeta di Riemann e la distribuzione dei numeri primi.
Il primo a notare l’importanza della funzione zeta nello studio dei numeri primi fu Eulero che, nel 1737, dimostrò l’identità, nota come prodotto di Eulero:

Grazie a questa formula,
Eulero dedusse che la serie

e quindi che
ad esempio
si può notare come il ragionamento di Eulero fornisca anche una diversa dimostrazione del
Nel secolo seguente
Čebyšëv e altri matematici si dedicarono allo studio della comprensione della distribuzione dei numeri primi, utilizzando per lo più metodi di combinatoria e la formula prodotto di Eulero, senza tuttavia riuscire a dimostrare la relazione asintotica

Fu però con Bernhard Riemann che la funzione zeta iniziò ad assumere un ruolo centrale nella teoria dei numeri. Nel suo unico articolo sull’argomento, Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse, Riemann considerò
I risultati principali ottenuti da Riemann furono:
-
la dimostrazione del fatto che la funzione  si possa prolungare analiticamente su tutto il piano complesso, ad eccezione di
si possa prolungare analiticamente su tutto il piano complesso, ad eccezione di  , in cui la funzione ha un polo semplice;
, in cui la funzione ha un polo semplice;
-
la scoperta di un’equazione funzionale (dimostrata in due diversi modi) che permette di mettere in relazione i valori della funzione zeta a destra e a sinistra della retta Re(s)=1/2;
-
una formula esatta che mostra la dipendenza della funzione enumerativa dei primi dagli zeri della funzione zeta.
-
L’introduzione di una nuova funzione olomorfa intera, ξ(s), strettamente legata alla ζ(s), e un abbozzo di dimostrazione di una formula prodotto per ξ(s) (questa formula fu dimostrata rigorosamente solo 34 anni dopo, da Jacques Hadamard).
Oltre a questi risultati,
Riemann diede alcune formule senza dimostrazione, tra cui una formula con una stima asintotica del numero di zeri non banali della funzione zeta, e scrisse che è “molto probabile” che tutti questi zeri abbiano parte reale uguale a 1/2.
Questa congettura ha preso il nome di ipotesi di Riemann ed è tuttora uno dei problemi aperti più importanti di tutta la matematica, grazie alle conseguenze che implicherebbe sulla distribuzione dei numeri primi.
Negli anni a seguire, vari matematici svilupparono ulteriormente le idee di Riemann, e fornirono dimostrazioni rigorose per alcune sue formule.
In particolare i risultati più importanti furono ottenuti da von Mangoldt e soprattutto da Hadamard e de la Vallée Poussin.
Questi ultimi infatti riuscirono a dimostrare che
la funzione zeta non ha zeri nella retta  e da questo ottenere come corollario il teorema dei numeri primi.
e da questo ottenere come corollario il teorema dei numeri primi.
Da allora, grossi sforzi sono stati fatti per dimostrare l’ipotesi di Riemann, ma sono stati ottenuti solo risultati parziali che restano molto lontani da quanto previsto da Riemann.
Nell’impossibilità di fare ulteriori progressi in questa direzione, lo sforzo dei teorici dei numeri si è spostato su altri importanti problemi relativi alla funzione zeta:
lo studio della crescita della funzione zeta lungo la retta critica,
lo studio dei suoi momenti e sulla trascendenza o razionalità dei suoi valori sui numeri naturali dispari.
Proprietà principali
Il grafico cartesiano della funzione zeta per i numeri reali tra -18,5 e 10
Il prodotto di Eulero
Una delle proprietà fondamentali della funzione zeta di Riemann, è il prodotto di Eulero,

valida per  , e dove il prodotto è effettuato su tutti i numeri primi
, e dove il prodotto è effettuato su tutti i numeri primi  .
.
La dimostrazione di questa identità usa solo
Infatti,
per  , si può calcolare la somma geometrica
, si può calcolare la somma geometrica

per ogni primo  .
.
Moltiplicando tra loro queste identità per tutti i primi  , per
, per  (questa ulteriore restrizione serve per assicurare la convergenza) si ha:
(questa ulteriore restrizione serve per assicurare la convergenza) si ha:

dato che per il teorema fondamentale dell’aritmetica
ogni numero naturale si può decomporre in maniera unica come prodotto di potenze di primi.
È interessante notare che la formula di Eulero ha come conseguenza che vi sono infiniti numeri primi.
Infatti,
se vi fosse solo un numero finito di numeri primi allora il prodotto di Eulero sarebbe un prodotto finito e quindi sarebbe definito anche per  , mentre in tale punto la funzione zeta ha un polo.
, mentre in tale punto la funzione zeta ha un polo.
Sebbene possa sembrare esageratamente complicata per un teorema di cui esistono dimostrazioni elementari, questa dimostrazione è molto importante in quanto una sua generalizzazione è stata usata da Dirichlet per dimostrare il teorema dell’infinità dei numeri primi nelle progressioni aritmetiche.
Questo prodotto è all’origine del collegamento tra funzione zeta e numeri primi.
Alcune serie correlate
Oltre alla serie che viene solitamente usata per definirla, la funzione zeta di Riemann è strettamente collegata anche con alcune altre serie di Dirichlet.
Tra queste, è di fondamentale importanza

che si ottiene derivando il logaritmo del prodotto di Eulero.
La funzione  è la Funzione di von Mangoldt, una funzione che è diversa da zero solo nelle potenze dei numeri primi.
è la Funzione di von Mangoldt, una funzione che è diversa da zero solo nelle potenze dei numeri primi.
Da questa identità si può ricavare facilmente, attraverso l’uso della somma per parti, la formula

dove

Altre serie di Dirichlet importanti collegate con la funzione zeta sono


dove  è il numero di rappresentazioni di
è il numero di rappresentazioni di  come prodotto di
come prodotto di  interi maggiori di
interi maggiori di  .
.
In particolare,


è legata alla funzione zeta di Riemann, tramite la relazione

e può essere usata per prolungare analiticamente la funzione zeta sul semipiano  .
.
Equazione funzionale
Una delle proprietà più importanti della funzione zeta di Riemann è che soddisfa la seguente equazione funzionale:

Per  di parte reale negativa, tutte le funzioni a destra dell’uguaglianza non hanno poli e negli interi pari, la funzione seno ha zeri semplici; da ciò segue che la funzione zeta ha zeri semplici (detti zeri banali) negli interi negativi.
di parte reale negativa, tutte le funzioni a destra dell’uguaglianza non hanno poli e negli interi pari, la funzione seno ha zeri semplici; da ciò segue che la funzione zeta ha zeri semplici (detti zeri banali) negli interi negativi.
Questa equazione può essere vista come una formula di riflessione rispetto a s = 1/2 e permette di esprimere la funzione zeta a sinistra della retta Re(s) = 1/2 in termine della funzione zeta a destra di tale retta e di alcune funzioni ben note.
La funzione zeta di Riemann si può “completare”, andando a formare la funzione Xi di Riemann,

che è olomorfa intera, ha gli stessi zeri della funzione zeta, ad eccezione degli zeri banali,
e soddisfa
l’equazione funzionale simmetrica

Gli zeri e l’ipotesi di Riemann
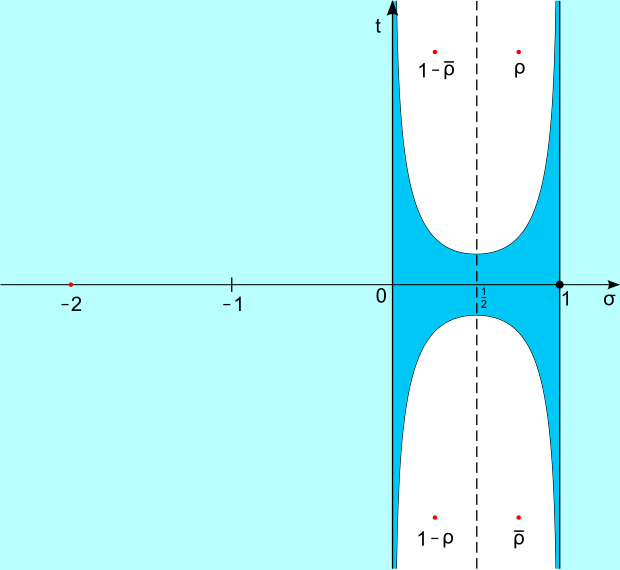
A parte gli zeri “banali”, presenti negli interi pari negativi, la funzione zeta non ha zeri a destra di σ=1 e a sinistra di σ=0 (né possono esserci zeri “vicini” a tali due rette). Inoltre, gli zeri non banali sono simmetrici rispetto alle rette σ=1/2 e t=0 e, secondo quanto ipotizzato da Riemann, appartengono tutti alla retta σ=1/2.
Il prodotto di Eulero ha come immediata conseguenza che la funzione zeta non ha zeri nel semipiano Re(s) > 1.
Inoltre,
grazie all’equazione funzionale, da ciò segue che gli unici zeri che la funzione zeta ha nel semipiano Re(s) < 0 sono gli zeri banali.
Gli zeri restanti possono quindi essere solo nella striscia 0 ≤ Re(s) ≤ 1 e, sempre grazie all’equazione funzionale, sono simmetrici rispetto a s = 1/2 e anche rispetto alla retta Im(s) = 0.
Di conseguenza, per ogni zero non banale σ + it ve n’è un altro in σ – it ed altri due in 1 -σ ± it (questi zeri coincidono con i precedenti se σ = 1/2).
Inoltre,
nelle loro dimostrazioni del teorema dei numeri primi, Hadamard e de la Vallée Poussin mostrarono che la funzione zeta non ha zeri neanche nella retta Re(s) = 1 (e dunque, per l’equazione funzionale, neanche in Re(s) = 0).
In particolare, tutti gli zeri non banali della funzione zeta sono nella striscia 0 < Re(s) < 1, che viene dunque detta striscia critica. Nella sua memoria del 1859,
Riemann ha espresso la sua convinzione che gli zeri siano disposti proprio al centro di tale striscia, nella retta Re(s) = 1/2 (la retta critica); questa congettura è tuttora aperta ed ha preso il nome di ipotesi di Riemann (in inglese Riemann hypothesis o RH).
I valori assoluti della funzione zeta nel piano complesso. A un valore più scuro corrisponde un valore assoluto più piccolo
L’ipotesi di Riemann è molto lontana dall’essere dimostrata e non è ancora noto se esista un ε > 0 tale che tutti gli zeri σ + it di ζ stiano in σ <1-ε (l’ipotesi di Riemann corrisponde a ε = 1/2 e, grazie al teorema di Hadamard e de la Vallée Poussin l’asserzione è dimostrata essere vera per ε = 0).
Tuttavia, qualche risultato parziale è stato ottenuto; il primo ad estendere la regione priva di zeri (zero-free region) è stato de la Vallée Poussin, che nel 1899 ha provato che gli zeri della funzione zeta di Riemann soddisfano la disequazione

per una costante  .
.
Questo risultato è stato leggermente migliorato nel corso degli anni,
Quest’ultimo nel 1958 ha dimostrato che

per t > 3 e per una costante C >0.
Se si eccettua per alcuni miglioramenti alla costante C (il più recente dei quali è dovuto a Ford, che ha dimostrato che si può prendere C = 1/57.54),
il teorema di Vinogradov è tuttora la migliore disuguaglianza nota per la regione priva di zeri.
La formula di Riemann-von Mangoldt
Nella memoria di Riemann è presente una stima asintotica per il numero di zeri non banali con parte immaginaria compresa tra  e
e  per
per  che tende all’infinito.
che tende all’infinito.
Definito

dove  denota la cardinalità dell’insieme, si ha
denota la cardinalità dell’insieme, si ha


Questa formula, enunciata da Riemann, è stata dimostrata da von Mangoldt nel 1905 ed è nota come
È chiaro che l’ipotesi di Riemann è vera se e solo se  coincide con
coincide con

Sono stati ottenuti alcuni risultati parziali in questa direzione,
i più importanti dei quali sono dovuti ad Hardy e Littlewood, che hanno provato che

a Selberg che ha provato che

per una qualche costante κ > 0,
e
e Conrey che hanno migliorato tale costante, portandola rispettivamente a 1/3 e poco più di 2/5.
Un’altra importante congettura sulla funzione zeta di Riemann (detta congettura degli zeri semplici o, in inglese, Simple Zeros Conjecture) asserisce che tutti gli zeri della funzione sono semplici.
I risultati ottenuti a proposito della percentuale degli zeri semplici sono molto simili a quelli per la percentuale degli zeri sulla retta critica ed anche in questo caso è stato provato che

per una costante κ* > 2/5.
Correlazione tra gli zeri
Dalla formula asintotica per N(T) è facile dimostrare che, assumendo l’ipotesi di Riemann, la distanza media tra due zeri consecutivi di ζ(s) ad altezza T è 2Π/log T.
Ci possono però essere intervalli insolitamente lunghi ed insolitamente corti senza zeri ed infatti, assumendo l’ipotesi di Riemann ed indicando con  l’n-esimo zero non banale (di parte immaginaria positiva) della funzione zeta di Riemann, si ha che esistono due costanti λ1 < 1 e λ2 > 1 tali che
l’n-esimo zero non banale (di parte immaginaria positiva) della funzione zeta di Riemann, si ha che esistono due costanti λ1 < 1 e λ2 > 1 tali che

e

Un’importante congettura sugli zeri della funzione zeta di Riemann è
la congettura della correlazione delle coppie di Hugh Montgomery (in inglese, pair correlation conjecture).
Questa congettura afferma che, per ogni β > α > 0, si ha
![\left\{\gamma ,\gamma '\in [0,T]\mid \zeta \left({\frac 12}+\gamma \right)=0,\zeta \left({\frac 12}+\gamma '\right)=0,\ {\frac {2\pi \alpha }{\log T))\leq \gamma -\gamma '\leq {\frac {2\pi \beta }{\log T))\right\}\sim N(T)\int _{\alpha }^{\beta }\left(1-\left({\frac {\sin \pi u}{u))\right)^{2}\right)\,du,](https://wikimedia.org/api/rest_v1/media/math/render/svg/438fe51ac9ac7c0e1c9f60e5671170832b4fa0c2)
per  che tende all’infinito.
che tende all’infinito.
Serie di Laurent
La funzione zeta di Riemann ha un polo semplice in s = 1, la sua serie di Laurent in tale punto è

dove le costanti sono chiamate costanti di Stieltjes e sono definite come:

Prodotto di Hadamard

Relazione con la funzione digamma

Relazione con la trasformata di Mellin
La trasformata di Mellin di una funzione  è definita come:
è definita come:

Essa è collegata alla funzione zeta.
Infatti:

Ciò equivale a dire che:

Questa rappresentazione converge per  e non può essere dunque usata per estendere il dominio della funzione.
e non può essere dunque usata per estendere il dominio della funzione.
Se π(x) è il numero di numeri primi compresi tra  e
e  allora possiamo scrivere che:
allora possiamo scrivere che:

E considerando la funzione  come
come  abbiamo che:
abbiamo che:

I valori della funzione zeta
L’immagine mostra i valori per la parte reale ed immaginaria di  con y che varia tra 0 e 50.
con y che varia tra 0 e 50.
Il calcolo dei valori esatti della funzione zeta è stato un compito piuttosto difficile:
Eulero riuscì nel 1735 ad avere una formula esatta per la funzione zeta di  .
.
Il suo metodo si poteva applicare per tutti gli  pari:
pari:
 ; la dimostrazione di questo fatto è la soluzione del problema di Basilea.
; la dimostrazione di questo fatto è la soluzione del problema di Basilea.


Più in generale è stato dimostrato che:

Non sono note formule analoghe, per i valori della funzione zeta in corrispondenza di  né per altri valori dispari (e maggiori di
né per altri valori dispari (e maggiori di  ) di
) di  .
.
Sommando i primi termini della serie che definisce la funzione zeta si possono però ottenere valori approssimati:



La razionalità e la trascendenza di questi valori è da molti anni al centro dell’interesse di molti studiosi di teoria dei numeri trascendenti.
Al 2014, non è noto se essi siano trascendenti o meno,
mentre
Ci sono inoltre altri risultati parziali sull’irrazionalità di queste costanti;
ad esempio,
è stato dimostrato che almeno uno tra ζ(5), ζ(7), ζ(9), e ζ(11) è irrazionale.
Altri valori





Il lavoro di Riemann
Molto prima che Hadamard e de la Vallée Poussin dimostrassero il teorema dei numeri primi, Bernhard Riemann pubblicò nel 1859 (come accennato) un articolo in cui trattava la funzione zeta.
Oltre a estendere il dominio della funzione tramite prolungamenti analitici Riemann, partendo dal Prodotto di Eulero, dimostrò una formula straordinaria che esprimeva appieno la correlazione tra numeri primi e funzione zeta

dove

e la serie sulla destra è sommata su tutti gli zeri non banali  della funzione zeta di Riemann.
della funzione zeta di Riemann.
La formula dà sempre un valore numerico reale anche se i  sono numeri complessi.
sono numeri complessi.
Questo è dovuto al fatto che le parti immaginarie degli zeri sono simmetriche rispetto all’origine.
In altre parole se ζ(a+bi)=0 anche ζ(a-bi)=0 e questa proprietà si estende anche a  .
.
Sommando dunque queste quantità la parte immaginaria si annulla.
Segue …
Read the rest of this entry »

























![{\ displaystyle {\ frac {1} {2T)) \ int _ {- T} ^ {T} dt | F (a + it) | ^ {2} dt = \ sum _ {n = 1} ^ {\ infty} [f (n)] ^ {2} n ^ {- 2a} {\ text {per)) T \ sim \ infty.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ea3980c0bc33096504d857d0a6648cc8b584aa4)
























































![\left\{\gamma ,\gamma '\in [0,T]\mid \zeta \left({\frac 12}+\gamma \right)=0,\zeta \left({\frac 12}+\gamma '\right)=0,\ {\frac {2\pi \alpha }{\log T))\leq \gamma -\gamma '\leq {\frac {2\pi \beta }{\log T))\right\}\sim N(T)\int _{\alpha }^{\beta }\left(1-\left({\frac {\sin \pi u}{u))\right)^{2}\right)\,du,](https://wikimedia.org/api/rest_v1/media/math/render/svg/438fe51ac9ac7c0e1c9f60e5671170832b4fa0c2)































 .
.
 é
é  risulti un
risulti un  e quindi, per la …
e quindi, per la …




















Devi effettuare l'accesso per postare un commento.