


°°°°°

ln questa lezione studieremo:
il problema di Cauchy,
il teorema di Cauchy in forma locale
il teorema di Cauchy in forma globale.
°°°°°
Problema di Cauchy
Il problema di Cauchy è la ricerca della soluzione di un’equazione differenziale che soddisfi certe condizioni iniziali.
Un problema di Cauchy per un’equazione differenziale del primo ordine
ha la seguente forma:
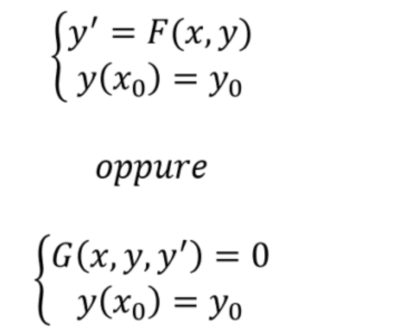
I due sistemi sono equivalenti, si tratta solo di scrivere in modo diverso l’equazione differenziale: nel primo caso c’è la y’ isolata al primo membro, mentre nel secondo caso non c’è (è inglobata in una funzione che chiamiamo G).

°°°°°
esempio 1
Tanto per farvi capire il concetto proviamo a risolvere il seguente problema di Cauchy:

Soluzione :
Risolviamo prima l’equazione differenziale
e
poi per trovare la costante che ci sarà useremo la condizione y(0)=1.
Intanto è
un’equazione a variabili separabili:
dobbiamo calcolare
la soluzione costante e poi quella generica.
La soluzione costante si ottiene mettendo y=k, quindi y’=0.
Si ottiene un’equazione molto semplice: 0=2xk^2, che è risolta per k=0.
Quindi
y = 0 sarà la soluzione costante.
Per trovare la soluzione generica separiamo le variabili e integriamo, come siamo abituati a fare:

Ora come vedete c’è una costante “c” che deriva dal fatto che abbiamo integrato.
Per capire quanto vale c usiamo la condizione iniziale che ci hanno fornito:

Con questa informazione possiamo scrivere
la soluzione del problema di Cauchy:

ATTENZIONE:
la soluzione costante che abbiamo trovato non è soluzione del problema di Cauchy,
ma è solo soluzione dell’equazione differenziale.
Una soluzione del problema di Cauchy deve essere tale per cui quando mettiamo x=0 otteniamo 1 (ce lo dice la condizione).
Siccome la soluzione costante è y=0, anche se poniamo x=0 otteniamo sempre 0 quindi non va bene.
Nella soluzione generica dell’equazione differenziale invece riusciamo a far quadrare i conti utilizzando la costante c.
°°°°°


Fine del teorema.
°°°°°
Ora cominciamo con la spiegazione:
intanto il concetto è che il teorema dice che
se valgono due condizioni allora esiste un’unica y che è soluzione del problema di Cauchy (in un determinato intervallo, cioè per determinati valori di x).
Il teorema, quindi, vi sta dando le condizioni per poter dire con sicurezza che
esiste una soluzione (unica) al problema di Cauchy.
Ora analizziamo bene le condizioni.

Come vedete, viene fuori un rettangolo.
All’interno del rettangolo, cioè per quei particolari valori di x e y, la funzione F deve esistere (e nell’ipotesi si dice che deve essere continua).
L’intervallo rettangolare appena disegnato si indica in formule scrivendo così:


In pratica se voi fate il rapporto incrementale rispetto ad y (cioè fatela divisione tra F(x, y_1)-F(x, y_2) e y_1-y_2) ottenete un numero minore di L, cioè avete un rapporto incrementale limitato.
Sappiamo che
il rapporto incrementale indica la derivata quindi in un certo senso state facendo la derivata rispetto ad y della funzione F(x, y) e vedete che essa è limitata, cioè non va ad infinito.
Questo significa
lipschitziana rispetto ad y.
Siccome la definizione di funzione lipschitziana è un pò brutta e noi per applicare il teorema dovremmo verificarla ogni volta, abbiamo una bella proposizione che ci aiuta.


Nel caso dell’esempio 1 abbiamo
F(x, y) = 2xy^2.
Rispetto ad y, tale funzione è C1 perché è un polinomio:
infatti la x va considerata costante dato che vogliamo controllare se è C1 rispetto ad y.
Questo ci fa avere un polinomio (di secondo grado perché c’è y^2) che è sempre derivabile con derivata continua.
La sua derivata parziale rispetto ad y, infatti, è 4xy che è continua.
Il fatto F(x, y) sia C1 e il fatto che essa sia continua in tutto il dominio (quindi anche in un intervallo rettangolare) fa sì che noi possiamo applicare il teorema di Cauchy e dire che di sicuro esiste una soluzione al problema di Cauchy. In effetti noi l’abbiamo trovata la soluzione.
Tale soluzione, dice il teorema, è definita in un intervallo (xo – δ, xo + δ).
Cosa vuol dire che la soluzione è definita in quell’intervallo?
Cominciamo dicendo che
xo è il punto in cui c’è la condizione iniziale, cioè nel nostro caso 0 perché avevamo y(0)=1.
Se noi disegniamo la soluzione che abbiamo trovato vediamo che c’è una parte di funzione compresa tra -1 e 1, cioè definita in un intervallo (0-1,0+1):

Il teorema ci sta dicendo che c’è una sola funzione che verifica il problema di Cauchy e tale funzione è derivabile in un intervallo.
Siccome noi l’abbiamo trovata, con il grafico possiamo vedere che effettivamente tale funzione è derivabile tra -1 e 1, come prevedeva il teorema.
In questo caso, quindi,
xo=0 e δ= 1.
Questo era solo un esempio, è una cosa teorica e la teniamo teorica.
°°°°°
Teorema di Cauchy:
forma globale
Nella forma locale la soluzione è definita in un intervallo (xo – δ, xo + δ).
Ciò significa che gli estremi non sono compresi.
Nella forma globale sono compresi anche gli estremi.

Ora diciamo il teorema di Cauchy in forma globale e poi lo spieghiamo.

Per la spiegazione ci manca la definizione di funzione sublineare quindi ora la diciamo.

Non indagheremo su questo teorema.
Entrambi i teoremi di Cauchy sono argomenti teorici che non sono fondamentali per gli esercizi.
Il teorema di Cauchy in forma globale ci fornisce le condizioni per dire che esiste un’unica soluzione globale al teorema di Cauchy, tutto qua.
Concludiamo così la lezione perché nella prossima lezione cominceremo a parlare del calcolo vettoriale e delle curve.
Segue …
Read the rest of this entry »
Tag: equazione differenziale, Problema di Cauchy, teorema di Cauchy in forma globale, teorema di Cauchy in forma locale



°°°°°

In questa lezione vediamo
le equazioni lineari del primo ordine,
il teorema di struttura.
°°°°°
equazione differenziale
se la funzione è di una sola variabile e l’equazione presenta soltanto derivate ordinarie
la funzione è a più variabili e l’equazione contiene derivate parziali della funzione stessa
°°°°°
Equazioni lineari del primo ordine
Un’equazione differenziale lineare del primo ordine è scritta nella seguente forma:
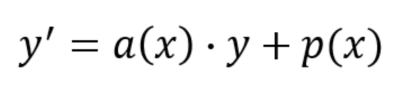
Sappiamo che la y dipende da x (quindi bisognerebbe scrivere y(x) e y'(x)) e che
l’obiettivo è calcolare la y.
Inoltre
a(x) e p(x) devono essere continue in un intervallo.
Per trovare le soluzioni di questo tipo di equazione consideriamo due casi separati:
(caso 1) il caso in cui p(x) è nullo
e
(caso 2) il caso in cui p(x) non è nullo
Soluzione: caso 1
Come primo caso ipotizziamo che p(x)=0.
In tal caso l’equazione si dice omogenea.
Per risolvere l’equazione notiamo che, con p(x)=0, essa risulta:

Otteniamo quindi un’equazione a variabili separabili che possiamo facilmente risolvere con quello che abbiamo visto nella Lezione 1.
Ricordiamo brevemente il metodo:
come prima cosa si cercano le soluzioni costanti; successivamente si “separano” le variabili (cioè si tiene in un membro quello che dipende da x e nell’altro membro quello che dipende da y) e si integrano entrambi i membri.
Troviamo le soluzioni costanti imponendo y=k, quindi y’=0.

C’è quindi una soluzione costante, ovvero y=0.
Adesso è giunta l’ora di separare le variabili:

Ricordiamo che
l’integrale di 1/y è il ln(|y|).
L’integrale di a(x) invece lo chiameremo A(x).
Proseguiamo con i conti mettendo anche un “+c” aggiuntivo dovuto agli integrali.
Dopo spieghiamo perché i conti vengono così.

Per passare dalla prima alla seconda riga abbiamo eliminato il logaritmo usando l’esponenziale come facevamo ai bei tempi di analisi 1.
Poi con le proprietà delle potenze sappiamo che se c’è la somma degli esponenti (in questo caso A(x)+c) possiamo fare una moltiplicazione tra due esponenziali.
Abbiamo poi posto c’ = e^c.
Questo è un passaggio che serve solo per migliorarci la visuale.
Bisogna stare attenti:
c’ è un’esponenziale, quindi è sempre maggiore di 0 (c’>0).
Per togliere il modulo basta aggiungere un “±” al secondo membro.
Poi abbiamo posto c” = ±c’.
Abbiamo quindi detto che c’ deve essere positivo.
Siccome c” è ±c’, esso può essere positivo o negativo.
Però non può essere nullo: c” ≠ 0.
Ciò è dovuto al fatto che c’ è sempre positivo ma non è nullo, quindi anche ±c’ non sarà nullo.
La morale è che abbiamo
una soluzione costante e un altro insieme di soluzioni non costanti:
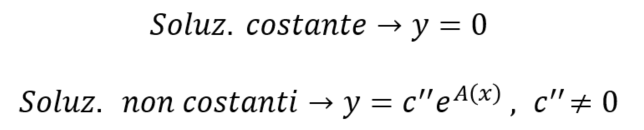
Da notare che
la soluzione costante può essere tranquillamente calcolata partendo da quella non costante e ponendo c” = 0.
Questo significa che possiamo scrivere che
la soluzione del caso 1 (ovvero p(x)=0) è la seguente:
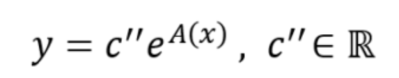
soluzione: caso 2
Cerchiamo le soluzioni dell’equazione lineare del primo ordine con p(x) ≠ 0.
Per trovare queste soluzioni utilizzeremo il metodo di variazione delle costanti.
Questo metodo consiste nel far variare le costanti (che scoperta!).
Abbiamo già trovato la soluzione dell’equazione omogenea (caso 1, quello con p(x)=0).
Essa dipende da una costante c”.
Con il metodo di variazione delle costanti ipotizziamo che questa soluzione vada bene anche quando p(x) ≠ 0.
A questo punto però variamo le costanti:
non scriviamo più c”, bensì scriviamo z(x),
cioè qualcosa che varia al variare della x.

Come vedete, abbiamo scritto z(x) e abbiamo ipotizzato che la y che otteniamo sia soluzione dell’equazione differenziale lineare del primo ordine.
Il nostro obiettivo sarà calcolare la z(x).
In pratica noi abbiamo ipotizzato che la soluzione dell’equazione sia simile a quella che abbiamo trovato con l’omogenea, cioè sia un’esponenziale.
Se la y che abbiamo scritto è soluzione dell’equazione, allora la verifica:
se “buttiamo dentro” la y che abbiamo trovato, l’equazione deve essere valida.
Nella y e nella y’ dell’equazione differenziale, allora, mettiamo rispettivamente
la y che abbiamo scelto noi e la sua derivata.
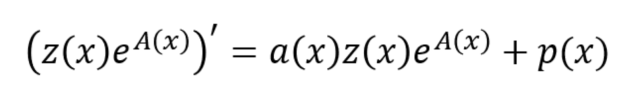
Adesso ci divertiamo a fare la derivata del primo membro.
ATTENZIONE:
dobbiamo derivare un prodotto, quindi useremo la regola del prodotto.
A secondo membro scriveremo sempre lo stesso pezzo perché per ora non ci interessa:
il nostro obiettivo è fare la derivata presente al primo membro.
Notate qualcosa di magico?
Cos’è A'(x)?
Sappiamo che A(x) è l’integrale di a(x), quindi A'(x) è la derivata dell’integrale di a(x).
Siccome la derivata e l’integrale sono due operazioni inverse, “si eliminano”:
A'(x) è semplicemente a(x).
Quindi ci sono due termini uguali, che si eliminano.

A questo punto il nostro obiettivo qual è?
E’ calcolare la z(x)
perché così poi noi sappiamo già che y dipende dalla z(x) e ci basterà sostituire quello che abbiamo trovato (adesso lo facciamo).
Per trovare z(x) scriviamo z'(x) come dz/dx.
In questo modo possiamo separare le variabili e integrare.

Abbiamo messo in evidenza la costante k che si ottiene dall’integrazione.
Adesso abbiamo finito perché sappiamo già com’è fatta la y
(l’abbiamo scritto all’inizio) e quindi possiamo scrivere la soluzione:

Scrivendola un po’ meglio otteniamo
la soluzione delle equazioni lineari del primo ordine:

NOTA BENE:
abbiamo trovato la soluzione.
Notate qualcosa di mega galattico?
Il secondo termine della somma (quello con la k e l’esponenziale) è la soluzione dell’equazione omogenea, cioè la soluzione del caso 1 che abbiamo fatto.
L’unica differenza è che invece che esserci scritto c” c’è scritto k,
ma sono due costanti e possiamo chiamarle come vogliamo.
°°°°°
Questo ci porta al teorema di struttura.
Segue …
Read the rest of this entry »
Tag: equazione differenziale, Equazioni lineari del primo ordine



°°°°°

In questa nostra prima lezione di Analisi Matematica 2 vediamo la definizione:
di equazione differenziale,
di equazione differenziale a variabili separabili,
di soluzione di un’equazione differenziale.
°°°°°
Equazione differenziale
Prima di dare la definizione di equazione differenziale spieghiamo intuitivamente cos’è.
Fino ad adesso abbiamo sempre visto equazioni in cui l’incognita è la “x”. L’obiettivo è quindi trovarsi la x. Nelle equazioni differenziali invece l’incognita è una funzione, quindi l’obiettivo sarà quello di trovarsi la funzione che verifica l’equazione differenziale.
Un’equazione differenziale è una relazione che coinvolge una funzione f insieme ad alcune sue derivate.
Se l’equazione coinvolge solo f ed f’ (che è la derivata prima di f) l’equazione si dice del primo ordine.
Facciamo subito un esempio banale:
Facciamo subito un esempio banale:

Quella che abbiamo appena scritto è un’equazione differenziale (perché coinvolge f e la sua derivata) del primo ordine (perché ci sono solo f ed f’). Intuitivamente sappiamo che una funzione che ha la derivata uguale a se stessa, cioè tale che f=f’, è la funzione l’esponenziale.
La costante c va messa perché quando si deriva c e^x si ottiene di nuovo c e^x e quindi l’equazione è verificata anche se moltiplichiamo l’esponenziale per una qualsiasi costante.
°°°°°
soluzione di un’equazione differenziale
facciamo il caso di un’equazione differenziale del primo ordine
Equazione del primo ordine:
Un’equazione del primo ordine può essere scritta nella seguente forma:

In questa equazione la funzione F è una qualsiasi funzione che dipende da x e da f.
Diamo la definizione di soluzione:
Se f è derivabile in un intervallo I, tale che
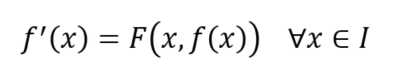
Allora
f si dice soluzione dell’equazione differenziale.
°°°°°
Equazione differenziale del secondo ordine:
Un’equazione del secondo ordine può essere scritta nella seguente forma:

Diamo quindi la definizione:
Se f è una funzione derivabile due volte in un intervallo I tale che

Allora
f si dice soluzione dell’equazione differenziale.
Siccome f dipende da x, diciamo che f deve verificare l’equazione per ogni x appartenente ad un intervallo.
°°°°°
equazione in forma normale
Un’equazione differenziale si dice in forma normale se al primo membro c’è solo la derivata di grado massimo.
In formule,
supponendo che l’equazione contenga le derivate di f fino alla derivata n-esima,
l’equazione in forma normale è scritta nel seguente modo:
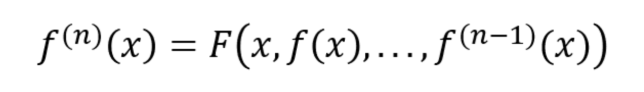
La derivata n-esima è indicata mettendo “(n)” come apice della f.
°°°°°
Equazione differenziale a variabili separabili
Cominciamo dicendo che la f(x) si indica anche con y.
Da analisi 1 sappiamo che y=f(x) quindi non dovreste stupirvi.
In pratica, quindi,
in un’equazione differenziale abbiamo due variabili:
la y e la x.
Il nostro obiettivo è trovare la y però essa dipende dalla x, infatti è f(x).
°°°°°
Un’equazione a variabili separabili è scritta nella seguente forma

Dove
a e b sono due funzioni continue rispettivamente in un intervallo I e in un intervallo J.
La definizione ci sta dicendo che riusciamo a dividere il secondo membro in una moltiplicazione tra un pezzo che dipende solo da x (chiamato a(x)) e uno che dipende solo da y (chiamato b(y)).
Metodo risolutivo
Il metodo è standard e si divide in due passi, che fanno in modo di trovare tutte le soluzioni possibili.
1. Soluzioni costanti
Cerchiamo le soluzioni costanti dell’equazioni a variabili separabili.
Ipotizziamo che b(y) sia uguale a zero
Imponiamo quindi y = k.
Sappiamo inoltre che
la derivata di una costante è 0, quindi y’ = 0.

La morale è che ci dimentichiamo del termine a(x) perché quello dipende da x, ma noi vogliamo trovare le y.
Teniamo quindi b(k)=0
e
lo risolviamo per trovare k, che è la nostra y dato che all’inizio abbiamo posto y=k.
2. Soluzioni non costanti
Ipotizziamo che b(y) sia diverso da zero (nel passo 1 l’abbiamo posto uguale a 0) così possiamo dividere entrambi i membri per b(y).
Sappiamo inoltre che per la cosiddetta notazione di Leibnitz
y’=d y/d x.
Scriviamo così:

Adesso possiamo integrare entrambi i membri.
Quando integriamo compare una costante, il classico “+c”.
Chiamiamo B(y) la primitiva di 1/b(y), cioè il suo integrale;
chiamiamo A(x) la primitiva di a(x).
Integrando otteniamo:

La prima riga è detta soluzione in forma implicita.
La seconda è detta soluzione in forma esplicita.
Il fatto che B sia invertibile è garantito dal fatto che B'(y)=1/b(y) è di sicuro diverso da zero quindi
B è strettamente monotona, dunque invertibile.
°°°°°
Questi sono dettagli.
esempio 1
Troviamo le soluzioni della seguente equazione differenziale:

Soluzione:
Intanto notiamo che è un’equazione a variabili separabili:
a primo membro ho solo y’
e
al secondo membro c’è una funzione che dipende dalla x (cioè x)
e
una che dipende dalla y (cioè y^2).
Dovremo quindi cercare le soluzioni costanti e quelle non costanti.
1. Le soluzioni costanti si trovano mettendo y=k, sapendo che y’=0.
Otteniamo:
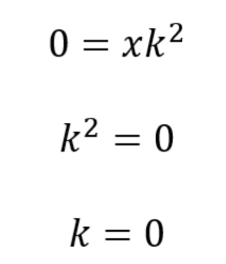
Abbiamo quindi una soluzione costante che è
y=0.
2. Adesso cerchiamo le soluzioni non costanti.
Dividiamo per y^2 in modo da “separare” le variabili.
Infatti
le equazioni hanno quel nome proprio perché si riesce ad avere un membro che dipende solo dalla y e uno che dipende solo dalla x.
Facciamo i conti:
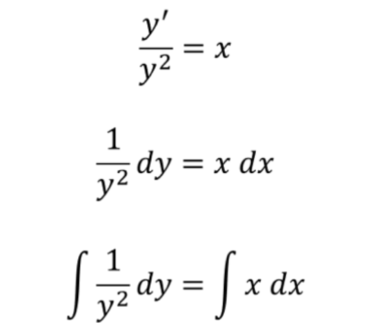
Adesso dobbiamo solo fare gli integrali e aggiungere il “+c”:

Ricordatevi le regole degli integrali:
1/y^2 = y^-2
e quindi il suo integrale è
-y^-1.
La conclusione è che abbiamo una soluzione costante (y=0) trovata al punto 1
e
un insieme di soluzioni trovato al passo 2.
Nota Bene:
Le soluzioni dipendono da una costante c, quindi
sono infinite e dipendono dai valori che assumerà quella costante.
°°°°°
esempio 2
Troviamo le soluzioni della seguente equazione differenziale:
E’ ancora una volta un’equazione a variabili separabili.
1. Le soluzioni costanti si trovano mettendo y=k, sapendo che y’=0. Otteniamo:
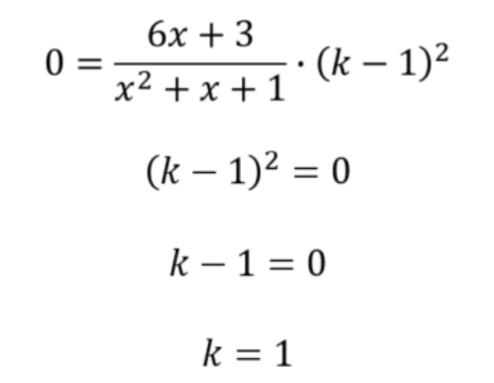
Abbiamo quindi una soluzione costante: y=1.
2. Adesso cerchiamo le soluzioni non costanti.
separiamo le variabili e integriamo.

Per l’integrale al secondo membro abbiamo sfruttato la regola:
il numeratore è la derivata del denominatore quindi risulta un logaritmo.
°°°°°
Segue …
Read the rest of this entry »
Tag: equazione differenziale, equazione differenziale a variabili separabili, soluzione di un’equazione differenziale

CALCOLO DIFFERENZIALE E INTEGRALE
‘‘ Non é la conoscenza, ma l’atto dell’apprendimento, e non il possesso, ma l’atto di arrivare fino alla meta, che ci garantisce il maggior godimento.-”
Carl Friedrich Gauss

In Analisi Matematica, un’equazione differenziale ordinaria (abbreviata in EDO, oppure ODE dall’acronimo inglese Ordinary Differential Equation) è un’equazione differenziale che coinvolge una funzione di una variabile e le sue derivate di ordine qualsiasi.

Come succede per tutte le equazioni differenziali, solitamente non è possibile risolvere esattamente una EDO e comunque non esistono metodi generali per farlo.
I diversi casi possibili sono pertanto analizzati singolarmente, e spesso ci si limita a studiare il comportamento qualitativo della soluzione senza che sia possibile ottenerne un’espressione analitica.
Particolarmente semplici risultano le equazioni lineari (di qualunque ordine) poiché si possono sempre ricondurre ad un sistema di equazioni lineari del primo ordine.
°°°°°
“Sono persuaso che la matematica sia il più importante strumento di conoscenza fra quelli lasciatici in eredità dall’agire umano, essendo la fonte di tutte le cose.”
(Cartesio)
°°°°°

…Segue…
“……..”
Tag: equazione differenziale, equazione differenziale ordinaria


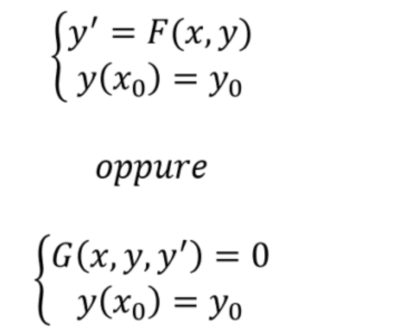




















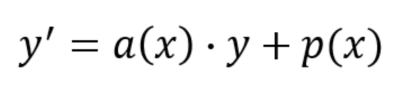




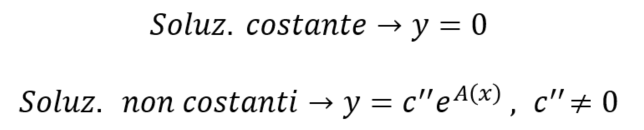
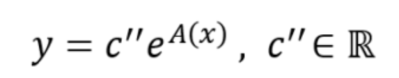

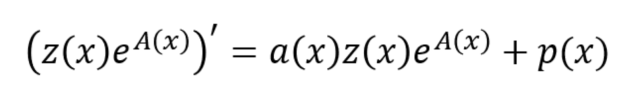





















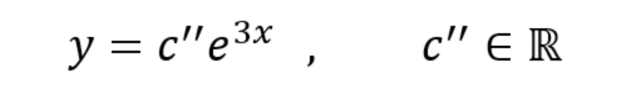




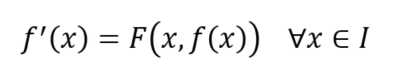


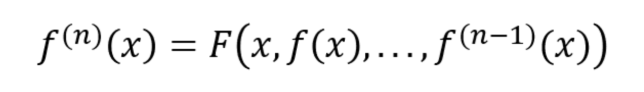





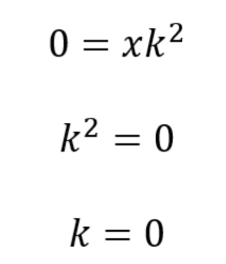
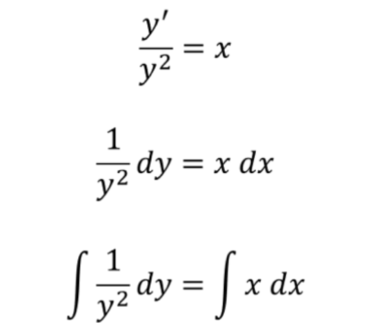








Devi effettuare l'accesso per postare un commento.