
°°°°°

Sono del tipo:
la cui soluzione (integrale) è semplicemente
l’integrale indefinito di f(x):

°°°°°

Un’equazione differenziale del primo ordine si dice
a variabili separabili
quando la derivata prima delle funzione incognita (y’) può scriversi come il prodotto di una funzione della sola variabile indipendente x e di una funzione della sola variabile y.
Dal punto di vista matematico,
un’equazione differenziale a variabili separabili può essere scritta con la seguente formula:
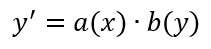
dove a(x) e b(y) sono due funzioni continue.
In parole povere, all’interno dell’equazione devono essere facilmente riconoscibili due blocchi tra loro moltiplicati, il primo può contenere come variabile solo la x, mentre il secondo può avere come variabile solo la y.

Esempio 1
Proviamo a fare qualche piccolo esempio per capire meglio come sono fatte queste particolari equazioni differenziali di primo ordine.
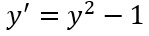
E’ un’equazione differenziale a variabili separabili? SI, perché al secondo membro abbiamo una funzione “y al quadrato meno uno” che è funzione solo della y. Manca la x?
Non c’è problema perché possiamo anche riscrivere la traccia come:
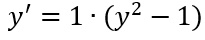
Quel termine 1 che abbiamo aggiunto con la moltiplicazione, è proprio la nostra a(x), ovvero la funzione che dipende solo da x. In questo caso è come se avessimo x elevato a 0 (ogni numero elevato a 0 fa 1)
Esempio 2
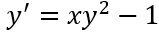
E’ un’equazione differenziale a variabili separabili? NO, perché in questo caso abbiamo una funzione in cui le variabili x e y non possono essere separate. Infatti non possiamo riconoscere direttamente un a(x) e un b(x) anche a causa di quel -1 finale.
COME RISOLVERE LE EQUAZIONI DIFFERENZIALI A VARIABILI SEPARABILI
Per determinare la soluzione, che in linguaggio matematico viene indicata anche come integrale generale, si procede con due semplici passaggi:
-
Si risolve b(y)=0. Il valore di y che ottieni sarà una prima soluzione dell’equazione differenziale.
-
Supposto b(y) diverso da 0, allora nella nostra traccia, al posto di y’, andremo a scrivere la derivata con la notazione di Liebniz:
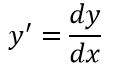
Così da poter riscrivere la traccia come:
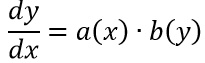
A questo punto, attraverso semplici passaggi algebrici, possiamo spostare dx al secondo membro, proprio accanto a a(x).
Contemporaneamente b(y) passa al primo membro accanto a dy.
Siamo pronti così per applicare l’integrale.
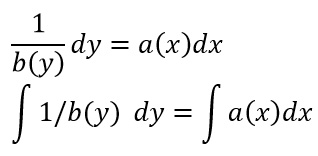
Non resta che risolvere i due integrali nel metodo che si ritiene più opportuno individuando le primitive A(x) e B(x) rispettivamente di a(x) e 1/b(y), aggiungendo la costante di integrazione c.
Sono particolari equazioni differenziali nelle quali è possibile esprimere

e separare nei due membri le due variabili e poi integrare separatamente.

Si dice che un’equazione differenziale del primo ordine è a variabili separabili se, posto
essa si può scrivere nella forma:

essendo q(x) e p(x) funzioni continue in opportuni intervalli.
°°°°°

Determinare l’integrale generale dell’equazione differenziale:
2 xy – y’ = 0
posto :
y’ = dy/dx
e supponendo
y ≠ 0
si ha:
2 xy – y’ = 0 ⇒ 2 xy – dy/dx=0 ⇒ 2 xy dx-dy=0 ⇒ dy = 2 xy dx ⇒ dy/y=2x dx
ora integrando ambo i membri si ottiene:
∫1/y dy = ∫ 2x dx ⇔ ln |y| +c_1= x^2+c_2 ⇔ ln |y| = x^2+(c_2 – c_1)
ln |y| = x^2+c ⇔ |y| = e^(x^2+c) ⇔ y = ±e^c · e^x^2
essendo c una costante arbitraria, e^c rappresenta un arbitrario numero reale positivo e quindi ±e^c rappresenta un un arbitrario numero reale diverso da zero, che pertanto si può indicare con k.
l’ultima equazione si può scrivere :
Osserviamo ora he, a causa della posizione fatta all’inizio del procedimento risolutivo (cioè y≠0) , é necessario verificare se anche la funzione di equazione y=0 é una soluzione della
2 xy – y’ = 0
In effetti, se y=0 , si ha y’=0 e dalla
2 xy – y’ = 0
si ottiene l’identità 0 = 0; quindi anche la funzione y=0 é un integrale della
2 xy – y’ = 0.
L’equazione di tale funzione dunque dalla
lasciando cadere la condizione k≠0 e quindi l’equazione 
esprime sinteticamente l’integrale generale della
2 xy – y’ = 0
°°°°°
Segue Esercitazione…

![]()




























Devi effettuare l'accesso per postare un commento.