
Salvatore Di Lucia


°°°°°
“La matematica non smetterà mai di stupirmi:
un prodotto della libera immaginazione umana che corrisponde esattamente alla realtà”.
Albert Einstein


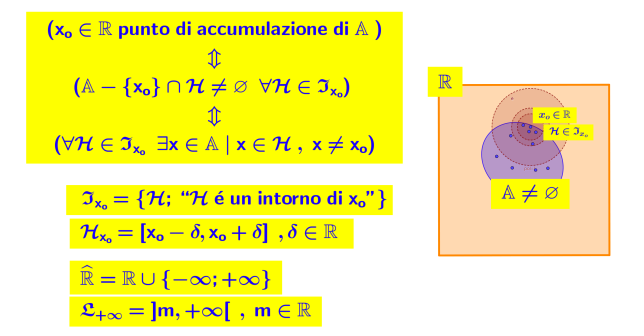
Punto di accumulazione
Un punto di accumulazione di un insieme reale E
è un punto x0 per il quale, comunque si scelga un intorno completo del punto stesso, esiste almeno un punto y dell’insieme E diverso da x0 e tale da appartenere all’intorno considerato.
In questa lezione vogliamo presentare la nozione di punto di accumulazione di un insieme in modo da iniziare a studiare le possibili relazioni tra punti e insiemi, con lo scopo successivo di studiare le proprietà dei sottoinsiemi reali a partire dall’analisi dei punti che li costituiscono, e non solo.
Definizione di punto di accumulazione
Consideriamo un generico insieme  , e sia
, e sia  un punto qualsiasi non necessariamente appartenente all’insieme.
un punto qualsiasi non necessariamente appartenente all’insieme.
Iniziamo col dare una definizione di punto di accumulazione che poi commentiamo con un po’ di esempi.
Diciamo che  è punto di accumulazione per l’insieme
è punto di accumulazione per l’insieme  se, comunque scelto un intorno completo
se, comunque scelto un intorno completo  , risulta che
, risulta che  contiene almeno un punto di
contiene almeno un punto di  diverso
diverso  .
.
In simboli matematici:

Una prima spiegazione sulla definizione di punto di accumulazione
Prestiamo attenzione alla definizione appena data, e soprattutto alle parole “comunque scelto un intorno completo”.
Per dire che un punto  è un punto di accumulazione per un insieme
è un punto di accumulazione per un insieme  non basta trovare almeno un intorno di
non basta trovare almeno un intorno di  tale da contenere almeno un punto di
tale da contenere almeno un punto di  che sia diverso da
che sia diverso da  .
.
La proprietà deve essere soddisfatta per qualsiasi intorno del punto  .
.
Trovare un intorno completo  che soddisfi la proprietà non basta,
che soddisfi la proprietà non basta,
infatti potrebbe esserci un intorno completo  più piccolo, dunque con raggio
più piccolo, dunque con raggio  , tale da non contenere alcun punto di
, tale da non contenere alcun punto di  che sia diverso da
che sia diverso da  .
.
Ad esempio
il punto  in figura non è di accumulazione per l’intervallo in nero […)
in figura non è di accumulazione per l’intervallo in nero […)
 Un esempio di punto che non è di accumulazione per un insieme (intervallo in nero).
Un esempio di punto che non è di accumulazione per un insieme (intervallo in nero).
Da una parte è vero che c’è un intorno (arancione) che contiene almeno un punto dell’intervallo nero che sia diverso da  ;
;
dall’altra però la proprietà richiesta deve valere per ogni intorno, e ad esempio nel caso dell’intorno rosso non è verificata.
Al contrario,
se nello stesso esempio proviamo a considerare come  un qualsiasi punto dell’intervallo, o eventualmente anche il suo estremo destro, intuiamo facilmente che la proprietà richiesta dalla definizione è verificata: comunque scegliamo un intorno completo del punto
un qualsiasi punto dell’intervallo, o eventualmente anche il suo estremo destro, intuiamo facilmente che la proprietà richiesta dalla definizione è verificata: comunque scegliamo un intorno completo del punto troviamo sempre almeno un altro elemento dell’insieme che sia diverso da x_o
troviamo sempre almeno un altro elemento dell’insieme che sia diverso da x_o tale da appartenere all’intorno considerato
tale da appartenere all’intorno considerato 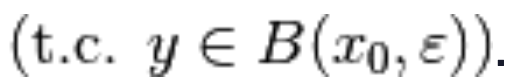
Esempi di punti di accumulazione
Esempio A
Il primo – nonché l’esempio di maggiore utilizzo in questi casi – consiste nel considerare la successione di valori reali definita nel modo seguente

vale a dire l’insieme


Diciamo che  è un punto di accumulazione per
è un punto di accumulazione per  .
.
Non vi fidate?
Molto bene, allora vediamo di stabilire se la definizione di punto di accumulazione è soddisfatta. 😉
Vogliamo mostrare che, comunque scegliamo un intorno completo di  , esso conterrà almeno un punto di
, esso conterrà almeno un punto di  diverso da
diverso da  stesso.
stesso.
Per riuscirci dobbiamo ragionare in astratto ed indipendentemente dalla lunghezza degli intorni.
Per dimostrare che vale la proprietà “contenere un altro punto di  che non sia
che non sia  “, non possiamo effettuare una verifica manuale per ogni possibile intorno, ossia per ogni possibile raggio
“, non possiamo effettuare una verifica manuale per ogni possibile intorno, ossia per ogni possibile raggio  .
.
Possiamo però fare una verifica in generale, quindi considerare il raggio dell’intorno come un parametro generico.
In questo modo, se riusciamo a dimostrare la proprietà con un generico intorno  , dove l’aggettivo generico è inteso come “con generico raggio”, allora la proprietà vale automaticamente per ogni intorno.
, dove l’aggettivo generico è inteso come “con generico raggio”, allora la proprietà vale automaticamente per ogni intorno.
In questo caso consideriamo  .
.
È vero che, comunque si scelga  , riusciamo a trovare un punto di
, riusciamo a trovare un punto di  diverso da
diverso da  e appartenente ad esso?
e appartenente ad esso?
Gli elementi di  sono della forma
sono della forma  ed è facile mostrare che, comunque scegliamo un raggio
ed è facile mostrare che, comunque scegliamo un raggio  , la proprietà è verificata:
, la proprietà è verificata:
basta considerare  in modo tale che risulti
in modo tale che risulti

ossia comunque scegliamo  è sufficiente considerare
è sufficiente considerare

per avere la proprietà di appartenenza.
Ad esempio,
se consideriamo  allora risulterà che ogni elemento
allora risulterà che ogni elemento  con
con  appartiene nell’intorno prefissato.
appartiene nell’intorno prefissato.
Dalla generalità del ragionamento consegue che la proprietà richiesta dalla definizione è verificata per ogni possibile intorno di  , per cui
, per cui  è un punto di accumulazione per
è un punto di accumulazione per  .
.
Di più:  è un punto di accumulazione dell’insieme pur non appartenendo all’insieme stesso.
è un punto di accumulazione dell’insieme pur non appartenendo all’insieme stesso.
Per il resto osserviamo che i punti dell’insieme  non sono punti di accumulazione per l’insieme stesso.
non sono punti di accumulazione per l’insieme stesso.
Per capirlo consideriamo ad esempio il primo elemento dell’insieme, cioè 1
(ottenuto per  ).
).
Il ragionamento si estenderà facilmente a tutti gli altri elementi dell’insieme.
Il punto 1 non è di accumulazione per  e per vederlo basta trovare un solo intorno di
e per vederlo basta trovare un solo intorno di  tale da non contenere altri punti di
tale da non contenere altri punti di  oltre a 1.
oltre a 1.
Se infatti la proprietà non vale anche per un solo intorno, allora la proprietà non vale per qualsiasi intorno:
in questo caso basta considerare l’intorno  e voilà, tale intorno non contiene alcun altro elemento dell’insieme.
e voilà, tale intorno non contiene alcun altro elemento dell’insieme.
Aspetti e conseguenze della definizione di punto di accumulazione che spesso sfuggono
1) Innanzitutto notiamo che, dato un punto di accumulazione  per un insieme
per un insieme  , in un suo intorno qualsiasi cade almeno un punto
, in un suo intorno qualsiasi cade almeno un punto  dell’insieme diverso da
dell’insieme diverso da  .
.
Poiché la proprietà deve valere per ogni intorno del punto, se ci concentriamo su uno specifico intorno possiamo restringerlo indefinitamente e continuare a trovare un punto  che appartenga ad esso.
che appartenga ad esso.
In sintesi, dato un punto di accumulazione, in ogni intorno cade almeno un punto  e quindi in ogni intorno cadono infiniti punti dell’insieme diversi da
e quindi in ogni intorno cadono infiniti punti dell’insieme diversi da  .
.
Nell’esempio,
se  è tale che
è tale che  , allora ogni elemento del tipo
, allora ogni elemento del tipo  con
con  apparterrà a
apparterrà a  .
.
2) Un punto di accumulazione per un insieme può non appartenere all’insieme stesso.
Non fatevi tradire dalla definizione:
leggendola distrattamente si potrebbe implicitamente fraintendere la scrittura

e pensare che  per essere di accumulazione debba necessariamente appartenere ad
per essere di accumulazione debba necessariamente appartenere ad  . Non è così:
. Non è così:
la definizione richiede che  e non che
e non che  .
.
Nell’esempio proposto
 non appartiene all’insieme
non appartiene all’insieme  , poiché non esiste alcun numero naturale per cui risulti
, poiché non esiste alcun numero naturale per cui risulti  .
.
Ciononostante esso è di accumulazione per  .
.
3) Lo abbiamo già scritto ma per sicurezza lo ribadiamo.
Per negazione della definizione, se troviamo anche un solo intorno per cui non vale la proprietà della definizione
(cioè se troviamo un intorno che non contiene alcun elemento dell’insieme e che non sia  )
)
allora la proprietà non vale per qualsiasi intorno.
In parole povere
per dimostrare che un punto non è di accumulazione per un insieme ci basta individuare un solo intorno all’interno del quale non ricade alcun elemento dell’insieme e che sia diverso dal punto stesso.
4) Signore e signori: il nome!
Un punto si dice di accumulazione per un insieme perché i punti dell’insieme si accumulano ad esso, non trovate? 🙂
Esempio B (punti di accumulazione di un intervallo)
Vediamo di espandere quanto scritto nel primissimo esempio post definizione.
Consideriamo un qualsiasi intervallo  .
.
Ogni punto contenuto nell’intervallo è un punto di accumulazione per l’intervallo stesso, ed è facilissimo vederlo.
Comunque consideriamo un intorno di un fissato punto  contenuto nell’intervallo, troviamo sempre almeno un punto
contenuto nell’intervallo, troviamo sempre almeno un punto  dell’intervallo tale da appartenere all’intorno e che sia diverso da
dell’intervallo tale da appartenere all’intorno e che sia diverso da  stesso. Facile, no?
stesso. Facile, no?

Qui notiamo che un punto di accumulazione per un insieme può appartenere all’insieme stesso.
Cosa succede con gli estremi di un intervallo?
Che siano inclusi (parentesi quadra) o esclusi (parentesi tonda), poco importa:
in tutti i casi sono sempre punti di accumulazione per l’intervallo stesso.
Consideriamo ad esempio l’intervallo ![(a,b]](image/gif;base64,R0lGODlhIwATAOMAAP///wAAAObm5nR0dEBAQGJiYp6enhYWFoqKiiIiIszMzAQEBAwMDFBQULa2tjAwMCH5BAEAAAAALAAAAAAjABMAAASxEEggxrw4603E/lfhTMPzTIUBgk4SZKd0rKuRwBJi0V/T4ICEgvc5qDCxhaZQGCBmH0EAgSggJslMYmcCIQJDwMIDOCkYmAG0vOP8JIujGX1ZtBfhDeMoHZUpShMKYBIOgRtSZF9YcBcOLxIFN0cZCocJb39BeWIeAgc/FgoPZBN0BmuaA20ABg1UowUej6ytrwVIEgI3RFc8MQANfjS+NMAABDwGpSvHFcREmtHRJQ8RADs=) .
.
Il punto  è di accumulazione per l’intervallo considerato:
è di accumulazione per l’intervallo considerato:
comunque scegliamo un intorno completo di  , la parte destra dell’intorno conterrà sempre almeno un punto dell’intervallo che non sia
, la parte destra dell’intorno conterrà sempre almeno un punto dell’intervallo che non sia  .
.
Lo stesso dicasi per  , in tal caso però dovremo fare riferimento alla parte sinistra dell’intorno completo.
, in tal caso però dovremo fare riferimento alla parte sinistra dell’intorno completo.
Generalizzazione
(i punti e gli estremi di un intervallo sono di accumulazione per l’intervallo stesso)
Tutti i punti di un intervallo non degenere, compresi gli estremi
(a prescindere che siano inclusi od esclusi), s
ono sempre di accumulazione per l’intervallo.
Più precisamente tutti e soli i punti di accumulazione di un intervallo sono dati dai punti appartenenti all’intervallo e dagli eventuali estremi esclusi dall’intervallo.
Esempio C
Ragioniamo infine sull’insieme

(intervallo unito a un singleton).
Qui è evidente che 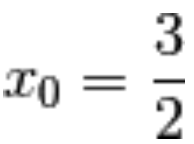 non è di accumulazione per
non è di accumulazione per  ,
,
infatti possiamo trovare almeno un intorno di 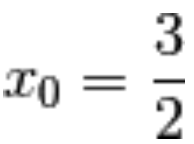 che non contiene alcun punto di
che non contiene alcun punto di  oltre al medesimo
oltre al medesimo 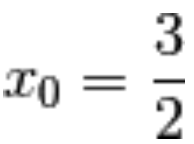 .
.
Uno a caso?
L’intorno  , infatti
, infatti

Come ormai sappiamo, se la proprietà non vale per uno specifico intorno non può valere per ogni intorno, quindi 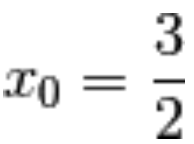 non è di accumulazione per
non è di accumulazione per  .
.
Un suggerimento spassionato
Ricordatevi sempre:
non fatevi spaventare quando in una definizione compare per ogni;
per verificarla è sufficiente effettuare una verifica in generale, trattando i parametri che compaiono (nel nostro caso specifico le lunghezze  degli intorni) come variabili.
degli intorni) come variabili.
Viceversa, per confutarla basta trovare un controesempio, cioè un esempio in cui la definizione non è soddisfatta.
Insieme derivato
Una pura formalità.
I nomi ci permettono di alleggerire il linguaggio, poco importa che sia scritto o parlato.
Vale dunque la pena di aggiungere un ulteriore tassello alla teoria e introdurre la nozione di insieme derivato di un insieme  , solitamente indicato con uno dei seguenti simboli
, solitamente indicato con uno dei seguenti simboli
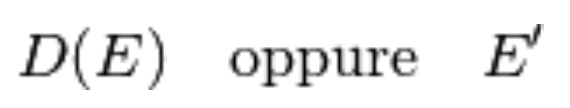
e definito come l’insieme dei punti di accumulazione dell’insieme  .
.
Qui ci fermiamo ma vogliamo anche lasciarvi qualche spunto di riflessione:
aiutandovi con qualche esempio creato ad hoc cercate di stabilire se:
– l’insieme derivato di un insieme  può essere contenuto nell’insieme
può essere contenuto nell’insieme  ;
;
– l’insieme derivato di un insieme  può contenere l’insieme
può contenere l’insieme  ;
;
e, in termini generali, di stabilire se è vero o non è vero che
– l’insieme derivato è sempre contenuto nell’insieme;
– l’insieme derivato contiene sempre l’insieme.
Ragionateci:
tutte le risposte sono scritte tra le righe dei precedenti esempi.
E a tal proposito, se volete leggerne altri: insieme derivato.
I punti di accumulazione ci serviranno per definire la nozione di insieme chiuso o insieme aperto, ma prima introdurremo altri tipi di punti che si definiscono con logiche analoghe ai punti di accumulazione.
La materia può sembrare spigolosa all’inizio, ma è sufficiente procedere con ordine e capire ogni singola parola delle definizioni, dove con ogni si intende tutte.
°°°°°

Tag: punto di accumulazione



°°°°°








°°°°°
Intervallo
Definizione
Formalmente,
un sottoinsieme  dei numeri reali
dei numeri reali  o di un altro insieme ordinato è un intervallo se per ogni coppia di elementi
o di un altro insieme ordinato è un intervallo se per ogni coppia di elementi  e
e  di
di  , ogni altro elemento
, ogni altro elemento  tale che
tale che  sta anch’esso in
sta anch’esso in  .
.
Osservazione
In  gli intervalli corrispondono agli insiemi convessi.
gli intervalli corrispondono agli insiemi convessi.
°°°°°
Insieme convesso
In uno spazio euclideo R^2
un insieme convesso è un insieme nel quale, per ogni coppia di punti, il segmento che li congiunge è interamente contenuto nell’insieme.
Esempi di
insiemi convessi :
mentre
Esempi di
insiemi non convessi:
qualunque insieme che contenga buchi,
incavature o che non sia connesso .
°°°°°
In uno spazio euclideo R^3
In tre dimensioni,
esempi di insiemi convessi sono
mentre
esempi di insiemi non convessi sono :
In termini più intuitivi una figura convessa è una figura “che esubera”, mentre una figura concava è una figura “che rientra”.
In insiemistica non si adopera la definizione di insieme concavo, bensì la nozione più articolata di
Nello studio delle funzioni , si può definire una funzione convessa come funzione il cui epigrafico è un sottoinsieme convesso del piano.
°°°°°
Spazi vettoriali
Sia
 uno spazio vettoriale .
uno spazio vettoriale .
Un insieme  si dice convesso se
si dice convesso se
per ogni coppia di punti  il segmento che li congiunge:
il segmento che li congiunge:
-

è interamente contenuto in  .
.
Un insieme bilanciato e convesso è detto assolutamente convesso .
Proprietà
-
Si può inoltre dimostrare che l’ intersezione di due insiemi convessi è ancora un insieme convesso. Infatti, siano X e Y due insiemi convessi, e A e B due punti appartenenti a .
-
Allora, siccome X è convesso e contiene sia A che B, contiene anche il segmento AB. Altrettanto si può dire di Y.
-
Quindi il segmento AB appartiene ad entrambi gli insiemi, e dunque alla loro intersezione.
-
Siccome questo ragionamento si può fare per ogni possibile scelta di 
, l’intersezione  è un insieme convesso.
è un insieme convesso.
-
Si dimostra che in ogni insieme  convesso, chiuso, non vuoto e contenuto in uno spazio di Hilbert esiste un unico elemento
convesso, chiuso, non vuoto e contenuto in uno spazio di Hilbert esiste un unico elemento  tale che:
tale che:

Esempi di insiemi convessi
Si consideri lo spazio euclideo . 
-
Un semispazio di  è il sottoinsieme
è il sottoinsieme  con
con  e
e  .
.
-
I semispazi sono sottoinsiemi convessi, infatti: dati due punti  , per ogni
, per ogni ![t \ in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)
si ha:
-

-
e quindi ,
-
Data una norma  su
su  e un numero reale
e un numero reale  ,
,
la palla chiusa  è un sottoinsieme convesso,
è un sottoinsieme convesso,
-
Data una norma  su
su  e un numero reale
e un numero reale  ,
,
il cono di norma è un sottoinsieme convesso.
è un sottoinsieme convesso.
°°°°°
Gli intervalli di  sono quindi gli insiemi seguenti
sono quindi gli insiemi seguenti
(dove  e
e  sono due numeri reali tali che
sono due numeri reali tali che  ):
):
-
 (intervallo aperto)
(intervallo aperto)
-
![{\displaystyle [a,b]=\{x|a\leq x\leq b\))](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7699e88cb19ad4a5895715dc300c68e4c837989) (intervallo chiuso)
(intervallo chiuso)
-
 (intervallo chiuso a sinistra)
(intervallo chiuso a sinistra)
-
![{\displaystyle (a,b]=\{x|a<x\leq b\))](https://wikimedia.org/api/rest_v1/media/math/render/svg/72b308336b45a70fd4d3cb8056e13ccfdc61185d) (intervallo chiuso a destra)
(intervallo chiuso a destra)
-
 (intervallo aperto infinito a destra)
(intervallo aperto infinito a destra)
-
 (intervallo chiuso infinito a destra)
(intervallo chiuso infinito a destra)
-
 (intervallo aperto infinito a sinistra)
(intervallo aperto infinito a sinistra)
-
![{\displaystyle (-\infty ,b]=\{x|x\leq b\))](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1018b912dd7df687d43e8cf46b1b539f9203c49) (intervallo chiuso infinito a sinistra)
(intervallo chiuso infinito a sinistra)
-
 (tutta la retta reale)
(tutta la retta reale)
-
![{\displaystyle [a,a]=\{a\))](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e5fc662e432a951ab083a879223c7446790c03b) (un punto)
(un punto)
-
I punti  e
e  sono gli estremi dell’intervallo.
sono gli estremi dell’intervallo.
Quindi
una parentesi quadra 
![{\displaystyle ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604326beb4b48cc622f2e386be688a2c3a8bf86a) indica che l’estremo appartiene all’intervallo,
indica che l’estremo appartiene all’intervallo,
mentre
una parentesi tonda 
 indica che non vi appartiene.
indica che non vi appartiene.
Una notazione alternativa usa ![{\displaystyle ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604326beb4b48cc622f2e386be688a2c3a8bf86a) e
e  rispettivamente al posto di
rispettivamente al posto di  e
e  .
.
Entrambe le notazioni fanno parte dello standard ISO 31-11 e del successivo ISO 80000-2 come equivalenti sebbene la notazione che prevede l’utilizzo delle parentesi tonde per indicare gli intervalli aperti sia in assoluto la più utilizzata.
I primi quattro intervalli hanno lunghezza  ,
,
i cinque seguenti hanno lunghezza infinita,
il punto e l’insieme vuoto hanno lunghezza  .
.
°°°°°
L’intervallo unitario è l’intervallo chiuso ![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) .
.
Proprietà
-
L’unione e l’intersezione di due intervalli aventi intersezione non vuota è un intervallo.
-
L’immagine di un intervallo mediante una funzione continua da  in
in  è ancora un intervallo.
è ancora un intervallo.
-
Un sottoinsieme della retta reale è un intervallo se e solo se è connesso.
-
Un intervallo è compatto se e solo se è del tipo ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) .
.
-
Ogni intervallo (anche infinito) è omeomorfo a uno, ed uno solo, di questi cinque intervalli:
°°°°°
Notazioni alternative
Raramente in ambito matematico, ma sovente in ambito ingegneristico,
il simbolo ÷, chiamato obelo, viene usato in Italia per indicare un intervallo numerico.
Ad esempio
3 ÷ 7 vuol dire ‘da tre a sette’, estremi compresi.
°°°°°
Insieme aperto

Il concetto di insieme aperto si trova in matematica in molti ambiti e con diversi gradi di generalità.
Intuitivamente,
un insieme è aperto se è possibile spostarsi sempre poco in ogni direzione a partire da ogni punto dell’insieme senza uscire dall’insieme stesso.
In realtà, seguendo le definizioni generali ci si può allontanare abbastanza da questa idea intuitiva; attraverso la definizione di insieme aperto si possono definire i settori come “vicino”, “lontano”, “attaccato”, “separato”;
Le definizioni non intuitive di insiemi aperti corrispondono a situazioni matematiche in cui questi utilizzati vengono utilizzati in modo non intuitivo.
°°°°°
Spazi topologici
La topologia è l’ambito più generale in cui si incontrano gli insiemi aperti;
in questo contesto il concetto di insieme aperto viene considerato fondamentale;
preso
un insieme X,
se
una qualunque collezione T di sottoinsiemi di X soddisfa le proprietà riportate sotto,
T viene chiamata topologia di X
e
gli insiemi di T , per definizione, i suoi aperti.
Perché
la collezione T sia una topologia deve valere:
-
l’ unione di una collezione arbitraria di insiemi di T è ancora un insieme di T
-
l’ intersezione di un numero finito di insiemi di T è ancora un insieme di T
-
l’insieme X e l’ insieme vuoto appartengono a T
Lo spazio topologico viene indicato specificando la coppia (X, T ).
È da notare che se si considera uno stesso insieme X con due diverse topologie T e T ‘ , si hanno due spazi topologici diversi; tuttavia in molti casi, in cui la struttura topologica emerge in modo “naturale”, indicare l’insieme è sufficiente per individuare lo spazio topologico.
°°°°°
Spazi metrici
un sottoinsieme  di
di  si dice aperto se, per ogni
si dice aperto se, per ogni  , esiste un numero reale
, esiste un numero reale  tale che i punti che distano da
tale che i punti che distano da  per meno di
per meno di  appartengono ancora a
appartengono ancora a  .
.
Formalmente:
se  , allora
, allora 
Gli aperti metrici così definiti costituiscono una topologia di  secondo la definizione precedente:
secondo la definizione precedente:
in questo modo
ogni spazio metrico è dotato in modo naturale di una struttura di spazio topologico, e tutti gli aperti metrici possono essere considerati aperti topologici (ma non viceversa).
°°°°°
Lo spazio euclideo  è un particolare spazio metrico.
è un particolare spazio metrico.
Un insieme aperto  dello spazio euclideo è un insieme tale che per ogni
dello spazio euclideo è un insieme tale che per ogni  di
di  esiste una palla di raggio
esiste una palla di raggio  centrata in
centrata in  , interamente contenuta in
, interamente contenuta in  .
.
In particolare,
un intervallo in  è aperto se è del tipo
è aperto se è del tipo  , dove
, dove  e
e  possono anche essere rispettivamente
possono anche essere rispettivamente  e
e  .
.
°°°°°
Insieme chiuso
Ogni definizione di insieme aperto corrisponde a una definizione di insieme chiuso .
In generale,
un insieme è chiuso se e solo se è il complementare di un insieme aperto;
gli spazi topologici questa è esattamente la proprietà definitoria, negli altri ambiti si danno definizione a parte e questa proprietà viene provata come un teorema .
°°°°°
Tag: Chiusura (topologia), Chiusura di un insieme, Frontiera (topologia), Insieme aperto, Insieme chiuso, Insieme chiuso-aperto, Insieme denso, Insieme derivato, Insieme discreto, Insieme limite, Insieme localmente chiuso, Insieme mai denso, Insieme perfetto, Intervallo, Intervallo in R^n, Intorno, Operatore di chiusura, Operatore parte interna, Parte interna, punto di accumulazione, Punto di aderenza, Punto di chiusura, punto isolato





 Un esempio di punto che non è di accumulazione per un insieme (intervallo in nero).
Un esempio di punto che non è di accumulazione per un insieme (intervallo in nero).




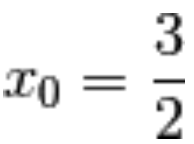 non è di accumulazione per
non è di accumulazione per 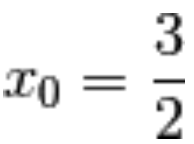 che non contiene alcun punto di
che non contiene alcun punto di 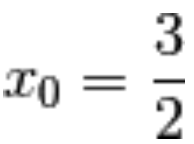 .
. , infatti
, infatti




























![]()



![]()

![]()
![]()
![]()




Devi effettuare l'accesso per postare un commento.