
°°°°°
Sezione conica
In matematica, e in particolare in geometria analitica e in geometria proiettiva,
con sezione conica, o semplicemente conica, si intende genericamente una curva piana che sia luogo dei punti ottenibili intersecando la superficie di un cono circolare con un piano.

Le sezioni coniche sono state studiate accuratamente in epoca ellenistica, in particolare da Menecmo ed Apollonio di Perga intorno al 200 a.C.; questi diede anche i nomi tuttora in uso per i tre tipi fondamentali di sezioni coniche: ellisse (la circonferenza ne è un caso degenere), parabola e iperbole.
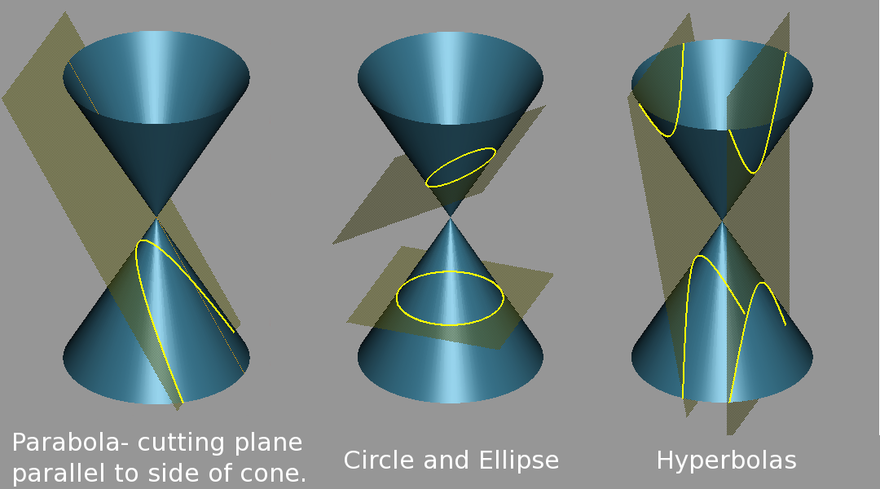
Tipi di sezioni piane di un cono
Si consideri il cono circolare retto costituito dalle rette generatrici che, con il suo asse, formano un angolo di ampiezza θ.
Si tenga presente che i punti del cono si tripartiscono in tre sottoinsiemi:
uno costituito solo dal suo vertice e
due sottoinsiemi separatamente connessi dette falde o nappe.
A seconda del tipo di piano che interseca il cono si hanno due tipi di curve:
le cosiddette non degeneri e le degeneri.
Per quanto riguarda le prime si può avere:
-
l’ellisse, ottenuta intersecando il cono con un piano che con il suo asse formi angoli maggiori di θ e minori o uguali a π/2; ciascuna di tali intersezioni appartiene a una sola delle due falde del cono ed è una curva chiusa;
-
la circonferenza, a sua volta caso particolare di ellisse ottenuta dall’intersezione del cono con un piano perpendicolare al suo asse, e anch’essa curva chiusa;
-
la parabola, ottenuta per intersezione del cono con un piano parallelo a una delle sue rette generatrici (in questo caso l’angolo formato con l’asse della conica è uguale a θ); ogni parabola appartiene a una sola delle falde del cono e non è una curva chiusa;
-
l’iperbole, ottenuta per intersezione del cono con un piano che formi con il suo asse un angolo inferiore a θ; anche l’iperbole è una curva aperta e, siccome il piano interseca entrambe le falde del cono, essa si bipartisce in due sottoinsiemi connessi detti rami della conica.
Le cosiddette coniche degeneri si ottengono, invece, per intersezioni con piani passanti per il vertice del cono:
-
il punto, ottenuto per intersezione del cono con un piano che formi con il suo asse angolo superiore a θ; nella fattispecie, il punto altro non è che il vertice di detto cono;
-
la retta, ottenuta per intersezione del cono con un piano che formi con il suo asse un angolo pari a θ; la retta ottenuta è una delle generatrici del cono;
-
una coppia di rette, ottenute per intersezione del cono con un piano che formi con il suo asse un angolo inferiore a θ; tali due rette si incontrano al vertice del cono e sono bisecate dalla retta ottenuta per intersezione del piano secante con il piano a esso ortogonale e passante per l’asse del cono.
Coniche ed equazioni quadratiche
Il grafico di ogni equazione quadratica in due variabili reali, se i coefficienti soddisfano determinate condizioni che preciseremo, individua una sezione conica di un piano cartesiano, cioè di un piano riferito ad un sistema di coordinate cartesiane.
Si trova inoltre che tutte le sezioni coniche si possono ottenere in questo modo.
Se si considera l’equazione quadratica nella forma
Visualizzazioni delle sezioni coniche
si ha la seguente casistica:
-
se l’equazione rappresenta una parabola;
-
se l’equazione determina una ellisse;
-
se e l’equazione rappresenta una circonferenza;
-
-
se l’equazione rappresenta una iperbole;
-
se l’equazione rappresenta una iperbole equilatera.
-
Condizione necessaria affinché la curva sia una circonferenza è che
Quello che si sta dicendo è che se l’equazione data non può rappresentare una circonferenza, se invece allora l’equazione potrebbe rappresentare una circonferenza.
Ciò implica che, ad esempio, non può essere l’equazione di una circonferenza, mentre invece potrebbe esserlo, tuttavia , perciò non esiste nessun punto che soddisfi l’equazione data.
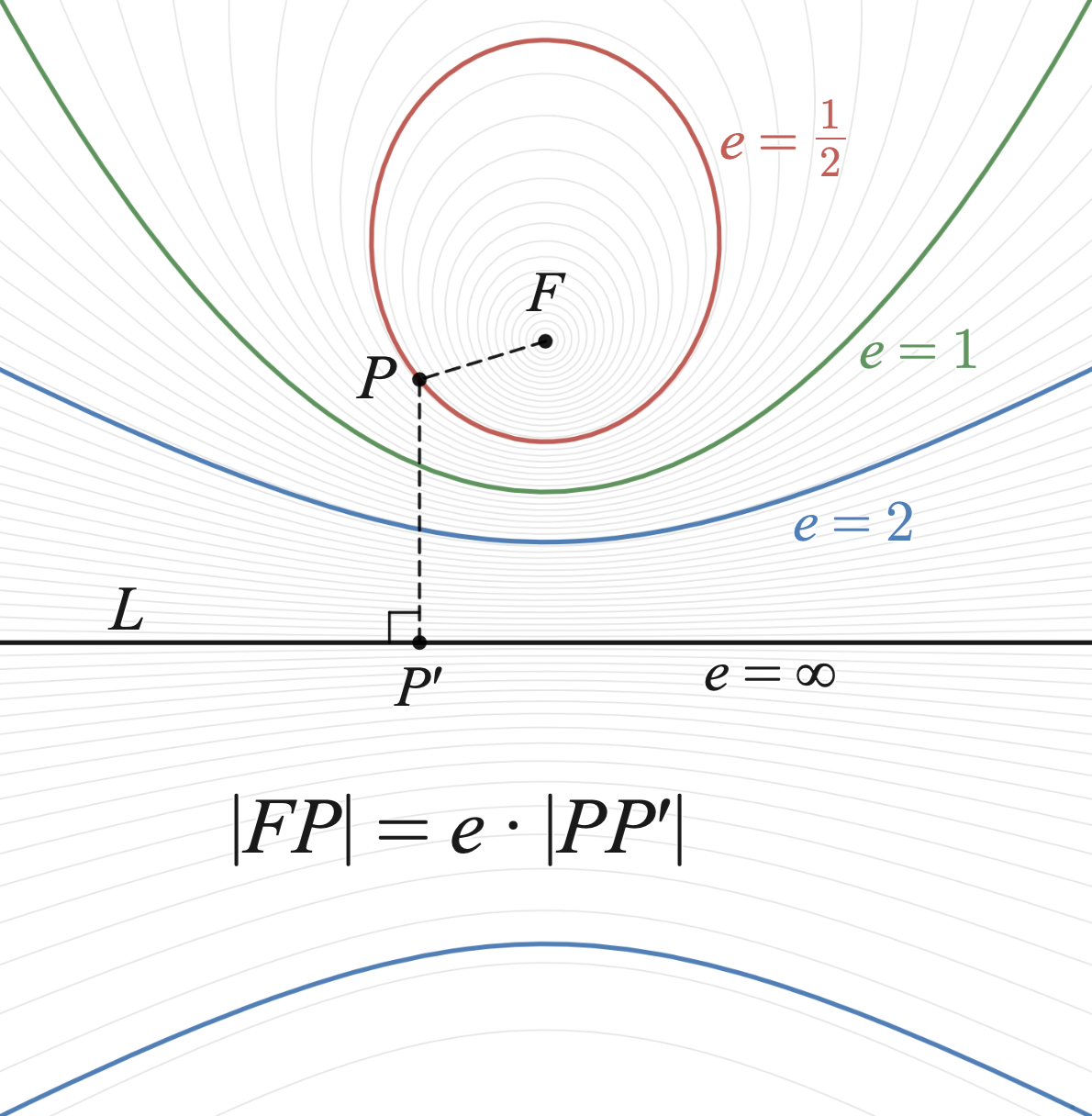
Eccentricità
Una definizione alternativa delle sezioni coniche viene data a partite da una retta , la direttrice, un punto esterno a , detto fuoco, e un numero , che prende il nome di eccentricità.
A tali enti si fa corrispondere la sezione conica consistente in tutti i punti la cui distanza da è uguale al prodotto di per la rispettiva distanza da .
Per si ottiene una circonferenza,
per un’ellisse,
per una parabola
per un’iperbole.
Per una ellisse e una iperbole si possono assumere due coppie fuoco + direttrice, ciascuna fornendo la stessa intera curva.
La distanza del centro dalla direttrice è , dove denota il semiasse maggiore dell’ellisse, oppure la distanza del centro da ciascuno dei punti di distanza minima dell’iperbole.
La distanza del centro da un fuoco è .
Nel caso della circonferenza si deve immaginare la retta direttrice a distanza infinita dal fuoco, cioè la retta si trova all’infinito del piano.
Questo caso non si può trattare a partire dalla richiesta che la circonferenza sia il luogo dei punti la cui distanza dal centro sia volte la distanza da , in quanto si avrebbe una forma indeterminata della forma zero per infinito; questo caso va trattato come caso limite di ellissi.
Si può dunque affermare che l’eccentricità di una sezione conica dia una misura di quanto essa si allontani dall’essere circolare.
Per una data lunghezza del semiasse maggiore, quanto più si avvicina a 1, tanto più piccolo è il semiasse minore.
Matrici associate alla conica
Sia l’equazione associata alla conica tale che Ad essa si associano due matrici e simmetriche tali che:
È possibile distinguere i diversi tipi di conica studiando il determinante delle due matrici:
Semiasse e coordinate polari

Semilato retto di un’ellisse
Si definisce semilato retto di una sezione conica C un segmento ortogonale all’asse maggiore che ha una estremità nel suo fuoco singolo o in uno dei suoi due fuochi e l’altra in un punto della C; la sua lunghezza di solito si denota con l.
Questa grandezza viene collegata alle lunghezze dei semiassi a e b dall’uguaglianza .
In coordinate polari, una sezione conica con un fuoco nell’origine e, se dotata di un secondo fuoco, con questo sul semiasse positivo delle x, è determinata dall’equazione
dove con si indica la distanza dall’origine/fuoco.
Applicazioni
Le sezioni coniche sono importanti in astronomia:
le orbite di due corpi (ipotizzando trascurabile l’effetto di altri corpi) che interagiscono secondo la legge di gravitazione universale sono sezioni coniche rispetto al loro comune centro di massa considerato a riposo.
Se tra di loro si esercita una attrazione sufficiente, entrambi percorrono un’ellisse;
se l’attrazione reciproca è insufficiente si muovono con la possibilità di allontanarsi illimitatamente percorrendo entrambi parabole o iperboli.
Si veda in proposito problema dei due corpi.
In geometria proiettiva le sezioni coniche nel piano proiettivo sono considerate equivalenti, nel senso che possono essere trasformate l’una nell’altra mediante una trasformazione proiettiva.
In epoca ellenistica la conoscenza delle coniche permise la costruzione di specchi parabolici, forse applicati in attività belliche (v. Specchi ustori) e nella costruzioni di fari di grande portata (v. Faro di Alessandria).
Sfere di Dandelin
Per una trattazione breve e abbastanza semplice delle sezioni coniche che mostra come esse si possono caratterizzare equivalentemente come intersezioni di un piano con un cono e in termini di fuochi o di un fuoco e una direttrice vedi Sfere di Dandelin.
Derivazione
Consideriamo un cono avente come asse l’asse delle z e il vertice nell’origine. Esso è determinato dall’equazione
dove
e denota l’angolo che ogni generatrice del cono forma con l’asse.
Si noti che questa equazione individua due superfici una posta al di sopra e l’altra al di sotto del vertice; nel parlare comune ciascuna di queste superfici viene detta cono;
i matematici preferiscono parlare di due nappe la cui unione costituisce il cono e la cui intersezione si riduce al vertice del cono.
Consideriamo un piano P che interseca il piano Oxy in una retta parallela all’asse delle y e che interseca il piano Oxz in una retta con una certa pendenza;
la sua equazione è
dove
e è l’angolo che P forma con il piano Oxy.
Ci proponiamo di individuare l’intersezione del cono con il piano P: ciò richiede la combinazione delle due equazioni (1) e (2).
Queste si possono risolvere nella variabile z e le espressioni trovate si possono uguagliare.
L’equazione (1) per la z fornisce
- ;
di conseguenza
Elevati al quadrato i due membri e sviluppato il binomio del membro a destra si ottiene
- .
Raggruppando le variabili si giunge alla
Si noti che questa è l’equazione della proiezione della sezione conica sul piano Oxy;
Quindi questa equazione fornisce una figura ottenuta dalla sezione conica mediante una contrazione nella direzione dell’asse delle x.
Derivazione della parabola
Si ottiene una parabola quando la pendenza del piano P è uguale alla pendenza delle generatrici del cono.
In questo caso gli angoli e sono complementari.
Questo implica che
di conseguenza
-
.
Sostituendo l’equazione (4) nell’equazione (3) si fa scomparire il primo termine nell’equazione (3) e rimane l’equazione
-
.
Moltiplicando entrambi i membri per a2,
-
;
a questo punto si può trovare un’espressione per la x:
L’equazione (5) descrive una parabola il cui asse è parallelo all’asse delle x.
Altre versioni della equazione (5) si possono ottenere ruotando il piano intorno all’asse delle z.
Derivazione dell’ellisse
Si individua un’ellisse quando la somma degli angoli e è inferiore ad un angolo retto, dunque un angolo acuto:
In tal caso la tangente della somma dei due angoli è positiva.
Ricordiamo ora la identità trigonometrica
-
;
questa implica
Ma m + a è positivo, in quanto è la somma di due numeri positivi; quindi la disuguaglianza (6) è positiva se anche il denominatore è positivo:
Dalla disuguaglianza (7) si deducono:
Riprendiamo ancora l’equazione (3),
ma questa volta assumiamo che il coefficiente di x2 non si annulli ma sia invece positivo.
Risolviamo per la y:
Questa equazione descriverebbe chiaramente un’ellisse, se non fosse presente il secondo termine sotto il segno di radice, 2 m b x: sarebbe l’equazione di una circonferenza dilatata proporzionalmente secondo le direzioni dell’asse delle x e dell’asse delle y.
L’equazione (8) in effetti individua un’ellisse ma in modo non evidente; quindi occorre manipolarla ulteriormente per convincersi di questo fatto. Completiamo il quadrato sotto il segno di radice:
- .
Raccogliamo i termini in b2:
Dividiamo per a ed eleviamo al quadrato entrambi i membri:
La x presenta un coefficiente, mentre è opportuno far scomparire tale componente raccogliendolo a fattore fuori del secondo termine che è un quadrato:
Un’ulteriore manipolazione delle costanti finalmente conduce a
- .
Il coefficiente del termine in y è positivo (per un’ellisse). Cambiando i nomi dei coefficienti e delle costanti ci conduce a
che è chiaramente l’equazione di un’ellisse.
In altri termini, l’equazione (9) descrive una circonferenza di raggio R e centro (C,0) che viene poi dilatata verticalmente per un fattore .
Il secondo termine del membro a sinistra (il termine nella x) non ha coefficiente ma è un quadrato, quindi deve essere positivo.
Il raggio è un prodotto di quadrati e quindi deve essere anch’esso positivo.
Il primo termine del membro a sinistra (il termine in y) ha un coefficiente positivo, e dunque l’equazione descrive un’ellisse.
Derivazione dell’iperbole
L’intersezione del cono con il piano P fornisce un’iperbole quando la somma degli angoli e è un angolo ottuso, dunque maggiore di un angolo retto.
La tangente di un angolo ottuso è negativa e tutte le disuguaglianze trovate per l’ellisse vengono cambiate nelle loro opposte.
Quindi si ottiene
Di conseguenza per l’iperbole si trova l’equazione che differisce da quella trovata per l’ellisse solo per avere negativo il coefficiente A del termine in y.
Questo cambiamento di segno fa passare da un’ellisse ad un’iperbole.
Il collegamento fra ellissi e iperbole può descriversi anche osservando che l’equazione di un’ellisse con coordinate reali può interpretarsi come l’equazione di un’iperbole con una coordinata immaginaria e, simmetricamente, che l’equazione di un’iperbole con coordinate reali può interpretarsi come l’equazione di un’ellisse con una coordinata immaginaria (vedi numero immaginario).
Il cambiamento di segno del coefficiente A equivale allo scambio fra valori reali e immaginari della funzione della forma y=f(x) che si legge nell’equazione (9).
Classificazione delle coniche reali in relazione ai loro punti impropri
Una ellisse non ha punti impropri. Una parabola ha un solo punto improprio. Una iperbole ha due punti impropri.
Segue …
Sfere di Dandelin
In geometria
una sezione conica non degenere, figura considerata come ottenuta dalla intersezione di un piano con un cono, possiede una o due sfere di Dandelin caratterizzate dalla proprietà:
-
una sfera di Dandelin è tangente sia al piano sia al cono.

Ogni sezione conica non degenere ha associata una sfera di Dandelin a ciascuno dei suoi due fuochi o al suo unico fuoco.
Teorema di Dandelin
L’interesse per le sfere di Dandelin viene dal seguente teorema:
-
il punto nel quale una sfera tocca il piano è un fuoco della sezione conica.
Dimostrazione:
si consideri l’illustrazione che raffigura un piano che interseca un cono in un’ellisse e mostra anche le due sfere di Dandelin.
Ciascuna sfera tocca il cono nei punti di una circonferenza.
Ogni sfera tocca il piano in un punto.
Denotiamo questi due punti con F1 ed F2.
Sia P un generico punto sulla ellisse.
Ci proponiamo di dimostrare che la somma delle distanze d(F1, P) + d(F2, P) rimane costante al muoversi del punto P lungo la curva.
La retta passante per P e il vertice del cono interseca le due circonferenze in due punti che denotiamo con P1 e P2.
Quando P si muove sull’ellisse, P1 e P2 si muovono ciascuno su una circonferenza.
La distanza tra Fi e P è uguale alla distanza tra Pi e P, poiché entrambi i segmenti appartengono a rette tangenti alla stessa sfera.
Di conseguenza la somma delle distanze d(F1, P) + d(F2, P) è uguale alla somma delle distanze d(P1, P) + d(P2,P). lunghezza del segmento fra P1 e P2.
Dato che P si trova sulla retta per P1 e P2, la precedente somma è uguale a d(P1,P2) e questa rimane costante al variare di P sull’ellisse; questo dimostra che gli Fi sono i fuochi dell’ellisse.
Questa argomentazione può essere adattata alle iperboli e alle parabole considerate intersezioni di un piano con un cono.
Un altro adattamento funziona per una ellisse ottenuta come intersezione di un piano con un cilindro circolare retto.
Conseguenze del teorema e sua dimostrazione
Se, come si fa spesso, si assume come definizione dell’ellisse quella di luogo dei punti P tali che d(F1, P) + d(F2, P) = a costante positiva, allora l’argomentazione precedente dimostra che l’intersezione di un piano con un cono è proprio un’ellisse. Che l’intersezione del piano con il cono sia simmetrica rispetto all’asse del segmento avente come estremità F1 ed F2 può risultare non intuitivo, ma l’argomentazione precedente lo rende chiaro.
°°°°°
Equazione di secondo grado
In matematica, un’equazione di secondo grado o quadratica ad un’incognita è un’equazione algebrica in cui il grado massimo con cui compare l’incognita è 2, ed è sempre riconducibile alla forma:
dove sono numeri reali o complessi.
Per il teorema fondamentale dell’algebra, le soluzioni (dette anche radici o zeri dell’equazione) delle equazioni di secondo grado nel campo complesso sono sempre due, se contate con la loro molteplicità.
Nel campo reale invece le equazioni quadratiche possono ammettere due soluzioni, una soluzione doppia, oppure nessuna soluzione.
Sono poi particolarmente semplici da risolvere le cosiddette equazioni incomplete, dove alcuni coefficienti sono uguali a zero.
Il grafico della funzione
nel piano cartesiano è una parabola, la cui concavità dipende dal segno di . Più precisamente: se la parabola ha la concavità rivolta verso l’alto, se la parabola ha la concavità rivolta verso il basso.
Storia
Gli antichi babilonesi lasciarono nelle tavolette di argilla le prime testimonianze della scoperta delle equazioni quadratiche e trovarono le prime tecniche per risolverle.
In Mesopotamia spesso le equazioni erano introdotte da problemi di tipo geometrico:
ad esempio si chiede di trovare il lato di un quadrato sapendo che l’area meno un lato è uguale a 870; problema che corrisponde alla nostra equazione (ridotta in forma normale come ).
I Babilonesi non accettavano però le soluzioni negative e nulle delle equazioni e, non accettando il fatto che i coefficienti potessero assumere valori sia positivi che negativi, non veniva riconosciuta nemmeno una forma normale unica, ma erano distinti tre casi con coefficienti positivi:
Espresse nella forma moderna la prima ha il termine noto negativo, la seconda il coefficiente di secondo grado negativo, e la terza entrambi i coefficienti minori di zero.
L’equazione con tutti i termini positivi non era nemmeno presa in considerazione in quanto ammette solo soluzioni negative.
Nella forma normale babilonese il coefficiente di secondo grado è unitario ma non arrivavano a tale forma, come successivamente gli arabi dividendo tutti i membri per .
Data, per esempio, l’equazione , entrambi i membri venivano infatti moltiplicati per : e poi veniva effettuata la sostituzione in modo da ottenere un’equazione in forma normale nella variabile ; .
Questo procedimento testimonia l’elevato grado di flessibilità raggiunto dall’algebra babilonese.
La soluzione era data tramite formule che ricordano molto quelle odierne.
Per esempio la formula risolutiva per il primo caso era, espressa in notazione moderna, la seguente:
che può essere ridotta tramite semplici passaggi algebrici alla formula risolutiva moderna per questo caso:
-
.
Il matematico indiano Baudhāyana, che scrisse un Shulba Sutras nell’antica India all’incirca nell’VIII secolo a.C., usò per primo equazioni quadratiche della forma e , indicando i metodi per risolverle.
I matematici babilonesi (intorno al 400 a.C.) e cinesi utilizzarono il metodo del completamento del quadrato per risolvere varie equazioni quadratiche con radici positive, ma non ottennero una formula generale.
Euclide descrisse un metodo geometrico più astratto intorno al 300 a.C.;
Diofanto di Alessandria si occupò della soluzione delle equazioni di secondo grado, tuttavia il suo lavoro non ebbe conseguenze significative poiché la matematica greca era in una fase di declino.
Il manoscritto di Bakshali, scritto in India fra il 200 a.C. e il 400 d.C., introdusse la formula risolutiva delle equazioni quadratiche.
Il primo matematico noto ad aver usato la formula algebrica generale, consentendo sia le soluzioni positive che quelle negative, fu Brahmagupta (India, VII secolo).
Al-Khwarizmi (BagdĀd, IX secolo d.C) sviluppò indipendentemente un insieme di formule che funzionava per le soluzioni positive.
Nell’al-Jabr, al-Khwarizmi distingue 5 tipi di equazione:
i tre già noti ai babilonesi
e
in più l’equazione pura e quella spuria Anche qui si pone il coefficiente di secondo grado uguale a , ma ci si arriva tramite divisione.
Le soluzioni negative non sono, nemmeno stavolta, accettate.
Il metodo usato da al-Khwarizmi è quello del completamento del quadrato.
L’equazione ,
per esempio,
sarebbe stata risolta aggiungendo a entrambi i termini in modo da “completare” il quadrato al primo membro: ossia .
Da questa si otteneva e si trovava così la soluzione positiva
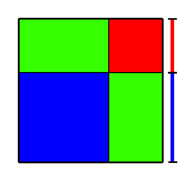
Il matematico arabo proponeva anche una trasposizione grafica.
Supponiamo di dover risolvere la stessa equazione .
Il metodo usato dal persiano in questo caso avrebbe potuto essere simile al seguente:
si tracci un quadrato che supponiamo avere lato (quello blu in figura).
Vi si affianchino due rettangoli di dimensioni e ossia (quelli verdi in figura).
L’area della figura verde e blu è
Poniamo ora che quest’area sia uguale a .
Aggiungiamo ora il quadratino rosso di lato , in modo da “completare” il quadrato grande.
L’area totale sarà quindi e il lato del quadrato grande è dunque 7.
Poiché il lato grande è dato dal lato del quadrato blu (cioè ) sommato al lato del rettangolo verde (cioè 4);
Al-Khwaritzmi pone per la prima volta l’accento sul segno del discriminante, che deve essere positivo perché l’equazione sia risolubile.
La priorità della scoperta della formula generale per risolvere un’equazione quadratica è stata attribuita a Sridhara (870-930 circa), sebbene ai suoi tempi vi sia stata una disputa. La regola (come riportata da Bhaskara II) è:
«Moltiplica entrambi i membri dell’equazione per una quantità nota uguale a quattro volte il coefficiente del quadrato dell’incognita; aggiungi a entrambi i membri una quantità nota uguale al quadrato del coefficiente dell’incognita; quindi determina la radice quadrata.[7]» |
Abraham bar Hiyya Ha-Nasi (conosciuto anche con il nome latino Savasorda) fu il primo a introdurre in Europa la soluzione completa con il suo Liber embadorum.
Nell’epoca moderna in Europa si iniziò ad accettare le soluzioni negative e, successivamente, quelle complesse e a porre l’equazione in un’unica forma normale.
Viète introdusse per primo delle lettere per esprimere i coefficienti delle equazioni, ipotizzando per primo che potessero assumere anche valori negativi.
Scoprì poi le formule che portano il suo nome e che mettono in relazione i coefficienti dell’equazione con le radici.
In particolare per l’equazione di secondo grado si afferma che se il coefficiente di secondo grado è 1, allora il prodotto delle radici dà il termine noto e l’opposto della loro somma il coefficiente di primo grado.
Cartesio introdusse nel XVII secolo la regola dei segni,
secondo la quale un’equazione di secondo grado ha tante soluzioni positive quanti sono i cambi di segno fra due coefficienti consecutivi. L’equazione , per esempio, ammette una soluzione negativa, invece ne ha due.
Equazioni quadratiche incomplete
Equazione spuria
Si dice spuria un’equazione quadratica che manca del termine noto, ossia avente la forma:
Un’equazione di questo tipo si risolve facilmente tramite il raccoglimento a fattor comune:
Per la legge di annullamento del prodotto quest’equazione è equivalente alle due:
e in definitiva le sue soluzioni sono:
Se i coefficienti dell’equazione spuria sono numeri reali, è caratteristica di questa equazione l’avere sempre due soluzioni reali distinte di cui una nulla.
Equazione pura
Si dice equazione quadratica pura un’equazione polinomiale di secondo grado mancante del termine di primo grado:
Portando al secondo membro e dividendo per si ottiene:
Se , l’equazione non ammette soluzioni nel campo reale, in quanto non esistono numeri reali che siano radici quadrate di un numero negativo (per esempio ), bensì esistono due soluzioni nel campo dei numeri complessi.
Se , l’equazione è risolta da:
Se i coefficienti dell’equazione pura sono numeri reali, le soluzioni saranno sempre o due numeri reali opposti oppure due numeri complessi coniugati.
Equazione monomia
Si dice equazione monomia un’equazione quadratica nella quale e , dunque nella forma In questo caso l’equazione ammette come unica soluzione doppia, o di molteplicità due, .
Equazioni complete e formula risolutiva generale
Un’equazione polinomiale di secondo grado viene detta equazione quadratica completa quando tutti i suoi coefficienti sono diversi da .
Essa viene risolta con il cosiddetto metodo del completamento del quadrato, così chiamato perché si modifica l’equazione fino a ottenere al suo primo membro il quadrato di un binomio nella forma:
Anzitutto si porti al secondo membro:
Moltiplicando per entrambi i membri, si ottiene:
Si noti che:
e che:
-
,
dunque è possibile considerare il termine come la della formula del quadrato di binomio e come il doppio prodotto dove la è uguale a ; dunque, per fare in modo che al primo membro si abbia un quadrato di binomio, si somma ad ambo i membri dell’equazione :
ovvero:
Il secondo membro di quest’equazione è detto discriminante e in genere viene indicato con la lettera greca (Delta).
Se è negativo non ci sono soluzioni reali dal momento che il primo membro, essendo un quadrato, è sempre maggiore o uguale a .
In caso contrario, si può scrivere:
che, con semplici passaggi, può essere riscritto come:
Quest’ultima espressione è nota come formula risolutiva delle equazioni di secondo grado.
Calcolo delle soluzioni
Alla luce della dimostrazione precedente è chiaro che, nella risoluzione di un’equazione quadratica, è anzitutto necessario calcolare il discriminante Si distinguono tre casi:
-
Se , vi sono due soluzioni reali e distinte:
-
-
Se , la formula risolutiva diventa:
Pertanto , e vi è una sola radice di molteplicità due.
-
-
Se , infine, l’equazione non ha soluzioni reali. In particolare le soluzioni sono sempre due, ma appartengono al campo dei numeri complessi: esse sono due numeri complessi coniugati e si calcolano tramite le due formule:
dove è l’unità immaginaria ().
-
Interpretazione geometrica
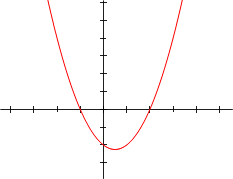
Per la funzione quadratica: , di una variabile reale , le ascisse dei punti dove il grafico tocca l’asse , e , sono le radici dell’equazione quadratica: .
Le radici dell’equazione quadratica
sono anche i punti in cui la funzione
assume valore nullo, dal momento che essi sono i valori di per cui:
Se , e sono numeri reali e il dominio di è l’insieme dei numeri reali, allora gli zeri di sono esattamente le ascisse dei punti dove il grafico di tocca l’asse x.
Dalle considerazioni precedenti si deduce che:
-
se il discriminante è positivo, il grafico interseca l’asse delle ascisse in due punti;
-
se è nullo, il grafico è tangente all’asse , ovvero lo interseca nel vertice della parabola;
-
se è negativo, il grafico non tocca mai l’asse .
Forma ridotta della formula risolutiva
La formula risolutiva dell’equazione di secondo grado può essere “semplificata” moltiplicando per il denominatore e il numeratore:
e, applicando la sostituzione , si ottiene:
Questa formula può risultare comoda quando il coefficiente dell’incognita di primo grado dell’equazione, , è esattamente divisibile per due, e viene chiamata formula ridotta.
Nel caso in cui , allora la formula si semplifica in:
Relazioni tra radici e coefficienti
Si ponga uguale alla somma delle due soluzioni dell’equazione quadratica e il loro prodotto, quindi e Sommando membro a membro le due soluzioni si ha:
Effettuando invece il prodotto membro a membro si ottiene:
Queste due relazioni consentono di determinare somma e prodotto delle radici senza risolvere l’equazione; esse sono un caso particolare delle formule di Viète.
Inoltre, se si riscrive la generica equazione di secondo grado nella cosiddetta forma normale, cioè dividendo ambo i termini per :
con banali sostituzioni si ottiene la forma:
Meno usata ma altrettanto importante è la relazione:
dimostrabile attraverso semplici passaggi algebrici.
Scomposizione in fattori del trinomio
Si consideri il polinomio completo di secondo grado:
e si supponga anche che il discriminante dell’equazione che si ottiene uguagliando a zero il polinomio sia positivo (ipotesi non necessaria nel campo dei numeri complessi).
Raccogliendo si ottiene:
Si è già trovato prima che e Dunque:
Pertanto è possibile scomporre un polinomio di secondo grado in due binomi di primo grado, calcolando le soluzioni dell’equazione data dal polinomio eguagliato a zero:
Se il
l’equazione associata ha una sola soluzione reale di molteplicità due, la scomposizione del trinomio di secondo grado può essere così riscritta:
Regola dei segni
La regola dei segni o regola di Cartesio consente di determinare il segno delle radici di un’equazione completa con discriminante non negativo.
Si considerino, nell’ordine, i segni di , e .
È possibile assumere che sia , a meno di moltiplicare entrambi i termini per .
Ci sono possibili combinazioni:
| a | b | c |
|---|---|---|
| + | + | + |
| + | + | – |
| + | – | + |
| + | – | – |
-
Primo caso: . Ricordando che e , segue che il loro prodotto è positivo e la loro somma negativa, per cui entrambe le soluzioni sono negative.
-
Secondo caso: e . Allora il prodotto delle radici è negativo (che implica che sono discordi) e la somma è negativa (che implica che la soluzione negativa è in valore assoluto maggiore di quella positiva).
-
Terzo caso: e . Allora il prodotto delle radici è positivo come pure la loro somma; pertanto entrambe le radici sono positive.
-
Quarto caso: e . Allora il prodotto delle radici è negativo (che implica di nuovo che sono discordi), ma la somma è positiva (dunque la soluzione positiva è maggiore in valore assoluto).
Chiamando permanenza ogni successione di due segni uguali e variazione ogni successione di segni contrari, è possibile riassumere i risultati precedenti affermando che
a ogni permanenza corrisponde una soluzione negativa,
e
a ogni variazione corrisponde una soluzione positiva.
Quando le radici sono discordi,
in valore assoluto è maggiore quella positiva se la variazione precede la permanenza;
quella negativa se la permanenza precede la variazione.
Esempio di risoluzione tramite completamento del quadrato
Sia:
allora:
da cui:
A questo punto è possibile disegnare il grafico di , traslando la parabola associata a di lungo l’asse , e di lungo l’asse .
Metodo del resto
Ad alcune equazioni possono essere applicati metodi diversi per trovarne le radici.
Si usa il teorema del resto di Ruffini, si controllano i divisori possibili del termine noto e si prendono una volta e una volta ; considerando poi la formula del teorema del resto di Ruffini , è possibile subito sapere che , e che sostituendo la nell’equazione al posto della si può verificare il resto che ci darà il polinomio diviso con :
se è allora sarà il divisore, dove una soluzione dell’equazione è .
A questo punto si può trovare l’altra soluzione in due modi:
-
Ruffini:
Applicando la divisione di Ruffini, o il metodo Canonico, per avere un binomio in cui il termine noto, cambiato di segno, sarà la seconda soluzione cercata:
Quindi:
-
Metodo delle radici:
Sapendo che:
e che:
-
,




























































![y=a{\sqrt {b^{2}-\left[x{\sqrt ((1 \over a^{2))-m^{2))}-{b \over {\sqrt ((1 \over a^{2}m^{2))-1))}\right]^{2}+\left({b^{2} \over {1 \over a^{2}m^{2))-1}\right)))](https://wikimedia.org/api/rest_v1/media/math/render/svg/69096001e49c9ba182db923fbcb7580c4d2caba8)
![y=a{\sqrt {b^{2}\left(1+{1 \over {1 \over a^{2}m^{2))-1}\right)-\left[x{\sqrt ((1 \over a^{2))-m^{2))}-{b \over {\sqrt ((1 \over a^{2}m^{2))-1))}\right]^{2))}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/55eaf4b2010aee30092ba5a1ba8d9d6a0f7baad1)




















































































































































Devi effettuare l'accesso per postare un commento.