“La matematica non conosce razze o confini geografici; per la matematica, il mondo culturale è una singola nazione.”
°°°°°
Insieme dei numeri razionali
In matematica, un numero razionale è un numero ottenibile come rapporto tra due numeri interi primi fra loro, il secondo dei quali diverso da 0.
Ogni numero razionale quindi può essere espresso mediante una frazione a/b, di cui a è detto il numeratore e b il denominatore. Sono ad esempio numeri razionali i seguenti:
 ,
,  ,
,  .
.
I numeri razionali formano un campo, indicato con il simbolo  , che sta per quoziente.
, che sta per quoziente.
In gran parte dell’analisi matematica i numeri razionali sono visti come particolari numeri reali, nel senso che esiste un isomorfismo tra i numeri reali dotati di parte decimale finita o periodica e i numeri razionali, il quale preserva la struttura di  come (sotto)-campo di
come (sotto)-campo di  ; i numeri reali che non sono razionali sono detti irrazionali.
; i numeri reali che non sono razionali sono detti irrazionali.
Ad esempio, sono irrazionali i seguenti:
 ,
,  ,
,  .
.
Nessuno di questi numeri può infatti essere descritto come rapporto di due numeri interi. I numeri  e
e  indicano rispettivamente la costante di Nepero e pi greco.
indicano rispettivamente la costante di Nepero e pi greco.
Mentre oggi spesso l’insieme dei numeri razionali è visto come sottoinsieme di quello dei numeri reali, storicamente e naturalmente i razionali sono stati introdotti prima dei reali, per permettere l’operazione di divisione fra numeri interi.
I numeri reali si possono introdurre servendosi dei numeri razionali in vari modi: mediante le sezioni di Dedekind, con una costruzione tramite successioni di Cauchy, con serie convergenti di numeri razionali.
In fisica, il risultato di una misurazione è solitamente esprimibile come numero razionale, dipendente dalla precisione dello strumento.
Storia
I numeri razionali (positivi[1]) furono il primo tipo di numeri, dopo i naturali (ossia gli interi positivi) ad essere riconosciuti come numeri e ad essere comunemente usati in matematica.
Gli antichi Egizi li usavano scomponendoli come somme di frazioni dal numeratore unitario (ancora oggi chiamate frazioni egiziane), rappresentandoli ponendo un simbolo sopra la rappresentazione dell’intero corrispondente; i Babilonesi usavano invece una scrittura posizionale (come per gli interi) a base sessagesimale.
Pitagora e i pitagorici basavano la loro concezione del mondo sui rapporti tra numeri interi, ovvero sui numeri razionali, e pensavano che ogni cosa esistente al mondo potesse essere ridotta a tali numeri: la loro scoperta dell’irrazionalità della radice quadrata di due distrusse questa concezione. Lo stesso concetto di “rapporto” non è del tutto chiaro nemmeno negli Elementi di Euclide, dove l’intero quinto libro è dedicato alla teoria delle proporzioni. Secondo le sue definizioni, un rapporto è un “tipo di relazione dimensionale tra due grandezze dello stesso tipo”[2], mentre due grandezze possono essere poste in rapporto se “esiste un multiplo intero della prima che supera l’altro”[3] (definizione dovuta probabilmente a Eudosso, che ricalca quello che viene oggi chiamato assioma di Archimede). L’uguaglianza di rapporti implica un’altra definizione complicata: in notazione moderna, equivale a dire che  se e solo se, dati due numeri m ed n, si ha che
se e solo se, dati due numeri m ed n, si ha che
- ma < nb implica mc < nd;
- ma = nb implica mc = nd;
- ma > nb implica mc > nd.
La definizione di grandezze commensurabili è invece la prima del libro X, e stabilisce che queste sono le grandezze che hanno una misura comune, ovvero sono multipli interi dello stesso numero.
La notazione decimale dei numeri fu introdotta da Stevino verso la fine del XVI secolo, sebbene lui non accettasse sviluppo decimali che non si concludessero, lasciando fuori così un gran numero di razionali. Più tardi Clavius e Nepero eliminarono questa limitazione.
Origine del termine
Il termine razionale deriva dal latino ratio, nel suo significato di rapporto.
Molte entità e strutture matematiche, come i polinomi o gli spazi vettoriali, nella loro definizione fanno riferimento ad un campo; l’aggettivo “razionale” attribuito ad una di queste entità è spesso usato per specificare che il campo scelto è quello dei numeri razionali. Per esempio si dice polinomio razionale ogni polinomio i cui coefficienti sono solo numeri razionali.
Va rilevato che sono dette operazioni razionali le quattro operazioni di addizione, sottrazione, moltiplicazione e divisione definite su strutture algebriche come i campi o gli anelli. Ne consegue che in vari casi l’aggettivo “razionale” riguarda entità ottenibili servendosi delle quattro operazioni razionali a partire da certi oggetti di base. Ad esempio si dicono funzioni razionali (in una o più variabili) le funzioni ottenibili componendo con operazioni razionali la variabile o le variabili e gli elementi di un campo.
Costruzione formale
Costruzione dei numeri razionali: ogni classe di equivalenza può essere rappresentata come una retta passante per l’origine, che passa per ogni coppia ordinata che rappresenta quel numero razionale.
Da un punto di vista formale, non è possibile definire i numeri razionali semplicemente come coppie di numeri interi (cioè come l’insieme delle frazioni del tipo  ), perché in questo caso, ad esempio, le coppie (3,2) e (6,4) sarebbero numeri diversi, mentre tra i razionali vale l’uguaglianza
), perché in questo caso, ad esempio, le coppie (3,2) e (6,4) sarebbero numeri diversi, mentre tra i razionali vale l’uguaglianza

È necessario quindi introdurre le nozioni di relazione e classe d’equivalenza, nel modo seguente.
Ogni numero razionale è una classe di equivalenza di coppie ordinate di numeri interi  , con
, con  diverso da zero. La relazione di equivalenza è la seguente
diverso da zero. La relazione di equivalenza è la seguente

L’addizione e la moltiplicazione di numeri razionali sono definite come

Si verifica che entrambe le operazioni così definite sono compatibili con la relazione di equivalenza: il loro risultato, infatti, non dipende dalle particolari coppie ordinate scelte per indicare i numeri razionali da sommare o moltiplicare. L’insieme quoziente di questa relazione è quindi Q.
Si noti che le operazioni ora definite non sono altro che la formalizzazione delle consuete operazioni tra frazioni:

Con le operazioni di cui sopra,  risulta un campo, ove la classe di
risulta un campo, ove la classe di  gioca il ruolo dello zero, e la classe di
gioca il ruolo dello zero, e la classe di  quello di uno. L’opposto della classe di
quello di uno. L’opposto della classe di  è la classe di
è la classe di  . Inoltre, se
. Inoltre, se  , ovvero la classe di
, ovvero la classe di  è diversa da zero, allora la classe di
è diversa da zero, allora la classe di  è invertibile, ed ha per inverso la classe di
è invertibile, ed ha per inverso la classe di  .
.
La classe di equivalenza corrisponde all’esistenza di più rappresentazioni come frazione dello stesso numero razionale:

per ogni k intero non nullo.
Possiamo definire anche un ordine totale su Q nel modo seguente:

Scrittura decimale
Come tutti i numeri reali, i numeri razionali possono essere rappresentati tramite il sistema numerico decimale. Lo sviluppo decimale dei numeri razionali ha la particolarità di essere periodico: un numero reale è razionale se e solo se nella sua scrittura esiste una sequenza finita di cifre (detta periodo) che si ripete all’infinito, da un certo punto in poi dopo la virgola.[4]
Si può facilmente dimostrare che nessun numero razionale, nel suo sviluppo decimale in base 10, può ammettere periodo 9.
Ad esempio:
 (si ripete il periodo “3” all’infinito)
(si ripete il periodo “3” all’infinito)


Un numero razionale può essere descritto quindi “soprallineando” il periodo, come in questi esempi.
Questa equivalenza tra razionali e numeri periodici implica che nessun numero razionale è normale in una qualunque base. Può essere usata anche per dimostrare l’irrazionalità di molti numeri: ad esempio

dove ogni 1 è separato da una sequenza di zeri di lunghezza crescente, è irrazionale in qualsiasi base, in quanto, se fosse razionale, il suo periodo conterrebbe una sequenza finita di zeri separati da 1. Tuttavia nell’espansione possono essere trovati gruppi di zeri di qualsiasi lunghezza, e quindi un periodo di tal genere non può esistere. Con metodi simili si può dimostrare che la costante di Copeland-Erdős  formata, in base dieci, dalla giustapposizione dei numeri primi, è irrazionale.
formata, in base dieci, dalla giustapposizione dei numeri primi, è irrazionale.
Questa tecnica è tuttavia inutile per provare l’irrazionalità di numeri non definiti in base alla loro espansione decimale, come  e pi greco.
e pi greco.
Frazioni continue
I numeri razionali hanno una rappresentazione in frazione continua semplice finita, e sono gli unici a possedere questa proprietà. Inoltre sono gli unici in cui la rappresentazione non è unica, ma doppia: ad esempio

Struttura algebrica
Munito di addizione, moltiplicazione e relazione d’ordine, l’insieme  ha la struttura algebrica di un campo ordinato archimedeo, e tuttavia non è un campo completo (si può dimostrare che il sottoinsieme
ha la struttura algebrica di un campo ordinato archimedeo, e tuttavia non è un campo completo (si può dimostrare che il sottoinsieme  ha come estremante superiore il valore
ha come estremante superiore il valore  , che non è un numero razionale).
, che non è un numero razionale).
L’unico sottocampo del campo dei numeri razionali è se stesso. Gli elementi neutri per la somma ed il prodotto sono rispettivamente 0 ed 1. La caratteristica del campo è 0; si può dimostrare inoltre che ogni campo con caratteristica 0 contiene un sottocampo isomorfo ai numeri razionali, e quindi che ogni campo di questo tipo può essere considerato come un’estensione dei razionali. In particolare, i razionali ne formano il sottocampo fondamentale.
La chiusura algebrica dei numeri razionali non è formata dai numeri reali, ma dai numeri algebrici, i quali formano uno spazio vettoriale di dimensione infinita sui razionali.
Il campo dei numeri razionali è inoltre il campo dei quozienti dell’insieme  dei numeri interi.
dei numeri interi.
I razionali come spazio metrico
Per il teorema di Ostrowski, i razionali sono uno spazio metrico rispetto solo a due tipi di valore assoluto: l’usuale modulo

e il valore assoluto p-adico

dove p è un qualsiasi numero primo e n è tale che  e a, b e p sono a due a due coprimi. Le norme riferiti a questi due valori assoluti sono rispettivamente
e a, b e p sono a due a due coprimi. Le norme riferiti a questi due valori assoluti sono rispettivamente

e

I razionali non sono completi rispetto a nessuna di queste due norme: i completamenti sono rispettivamente i numeri reali e i numeri p-adici. Quest’ultimo è particolarmente usato in teoria dei numeri, mentre l’introduzione dei numeri reali è necessaria per poter stabilire alcuni teoremi fondamentali dell’analisi, tra cui il teorema degli zeri e il teorema di Weierstrass.
Numerabilità
Schema che illustra la dimostrazione di Cantor: le frazioni in rosso sono quelle che non rappresentano nuovi numeri razionali.
 è numerabile, cioè esiste una corrispondenza biunivoca tra i razionali e i numeri naturali. Questo risultato, apparentemente paradossale (è naturale, infatti, pensare che le frazioni siano “molte di più” degli interi), è stato dimostrato da Georg Cantor. Il suo ragionamento si basa sul diagramma a fianco: possiamo infatti ordinare i razionali positivi, seguendo le frecce, in modo che ad ognuno di essi sia assegnato un numero naturale[5]; anzi, ogni numero sarà contato infinite volte (perché ognuno ha un’infinità di rappresentazioni diverse), ma questo non può rendere l’insieme
è numerabile, cioè esiste una corrispondenza biunivoca tra i razionali e i numeri naturali. Questo risultato, apparentemente paradossale (è naturale, infatti, pensare che le frazioni siano “molte di più” degli interi), è stato dimostrato da Georg Cantor. Il suo ragionamento si basa sul diagramma a fianco: possiamo infatti ordinare i razionali positivi, seguendo le frecce, in modo che ad ognuno di essi sia assegnato un numero naturale[5]; anzi, ogni numero sarà contato infinite volte (perché ognuno ha un’infinità di rappresentazioni diverse), ma questo non può rendere l’insieme  più grande. Lo stesso argomento può essere usato per dimostrare che i razionali negativi sono numerabili. Poiché l’unione di due insiemi numerabili è ancora numerabile,
più grande. Lo stesso argomento può essere usato per dimostrare che i razionali negativi sono numerabili. Poiché l’unione di due insiemi numerabili è ancora numerabile,  risulta essere numerabile.
risulta essere numerabile.
Al contrario, l’insieme dei numeri reali non è numerabile, e quindi “quasi tutti” i numeri reali sono irrazionali. Questo implica che, sebbene  sia denso in
sia denso in  , abbia misura di Lebesgue nulla.
, abbia misura di Lebesgue nulla.
Polinomi
L’anello dei polinomi a coefficienti razionali si indica con ![{\mathbb {Q))[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/59f611a32bc84287517e9f4b283ac998c0394479) . Al contrario dei polinomi a coefficienti reali o complessi, non esiste un criterio semplice per individuare l’eventuale irriducibilità di un polinomio a coefficienti razionali.
. Al contrario dei polinomi a coefficienti reali o complessi, non esiste un criterio semplice per individuare l’eventuale irriducibilità di un polinomio a coefficienti razionali.
La maggior parte dei criteri usati si basano sul lemma di Gauss, il quale afferma che un polinomio a coefficienti interi è riducibile nell’anello ![{\mathbb {Q))[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/59f611a32bc84287517e9f4b283ac998c0394479) se e solo se è riducibile in fattori di grado maggiore di 0 nell’anello
se e solo se è riducibile in fattori di grado maggiore di 0 nell’anello ![{\mathbb {Z))[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a538d203a057d4c604f799c28e9a7be410fdcac) dei polinomi a coefficienti interi. Poiché ogni polinomio a coefficienti razionali può essere trasformato in uno a coefficienti interi moltiplicando per il massimo comun divisore dei denominatori senza cambiare la sua irriducibilità, questo lemma permette di applicare ai polinomi a coefficienti razionali alcuni criteri, come il criterio di Eisenstein, che si applicano sui polinomi a coefficienti interi.
dei polinomi a coefficienti interi. Poiché ogni polinomio a coefficienti razionali può essere trasformato in uno a coefficienti interi moltiplicando per il massimo comun divisore dei denominatori senza cambiare la sua irriducibilità, questo lemma permette di applicare ai polinomi a coefficienti razionali alcuni criteri, come il criterio di Eisenstein, che si applicano sui polinomi a coefficienti interi.
In particolare, questo criterio permette di costruire polinomi irriducibili di qualunque grado: ad esempio

è irriducibile. Questo non avviene negli anelli di polinomi a coefficienti reali o complessi: nel primo caso i polinomi irriducibili possono essere solamente di primo o di secondo grado, mentre nel caso complesso, in conseguenza del teorema fondamentale dell’algebra, ogni polinomio si scompone in fattori di primo grado.
Radici razionali
Al contrario di quanto avviene con le radici reali (o complesse), esiste un algoritmo molto veloce per stabilire quali siano (se esistono) gli zeri razionali di un polinomio (a coefficienti interi, forma a cui può essere ridotto ogni polinomio a coefficienti razionali). Il teorema delle radici razionali afferma infatti che, se

con gli  interi, allora, nelle eventuali radici razionali p/q, p è un divisore di
interi, allora, nelle eventuali radici razionali p/q, p è un divisore di  e q di
e q di  . Poiché i divisori di questi due numeri sono in numero finito, sarà sufficiente, per il teorema del resto, controllare se per ogni coppia di divisori si ha P(p/q)=0 (nel qual caso p/q è una radice) oppure no.
. Poiché i divisori di questi due numeri sono in numero finito, sarà sufficiente, per il teorema del resto, controllare se per ogni coppia di divisori si ha P(p/q)=0 (nel qual caso p/q è una radice) oppure no.
Razionali complessi
I razionali complessi, o razionali gaussiani per analogia con gli interi gaussiani, sono quei numeri complessi nella forma a+ib, dove a e b sono razionali e i rappresenta l’unità immaginaria. L’insieme dei razionali gaussiani forma un campo, che è il campo dei quozienti dell’anello degli interi gaussiani.Tale insieme si denota generalmente con  , cioè il più piccolo campo contenente i razionali e l’unità immaginaria i.
, cioè il più piccolo campo contenente i razionali e l’unità immaginaria i.
Approssimazioni razionali
Read the rest of this entry »



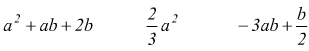
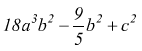 è un polinomio intero
è un polinomio intero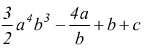 è un polinomio fratto
è un polinomio fratto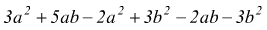
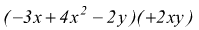
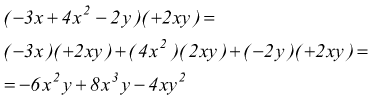
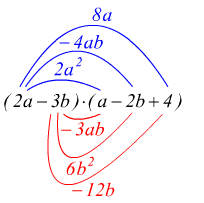
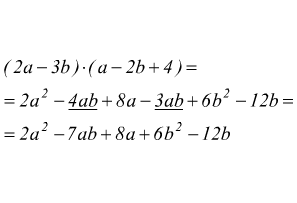
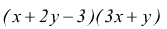
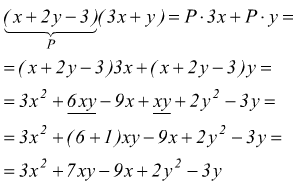
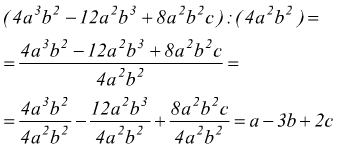
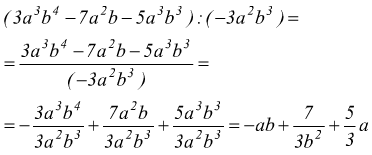
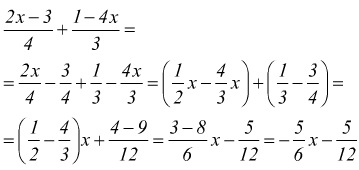

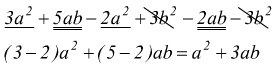

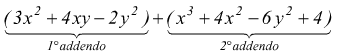
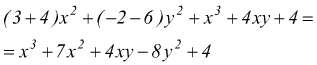
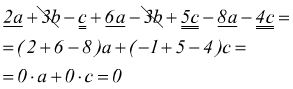
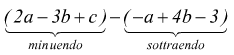
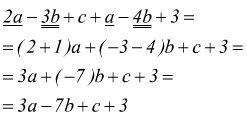





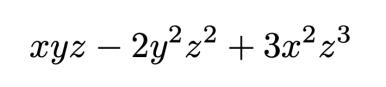 è di grado 5, dato che i monomi sono rispettivamente di grado 3,4,5.
è di grado 5, dato che i monomi sono rispettivamente di grado 3,4,5.



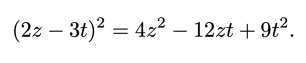
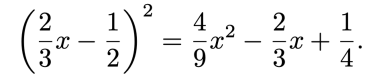






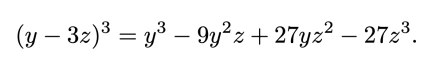







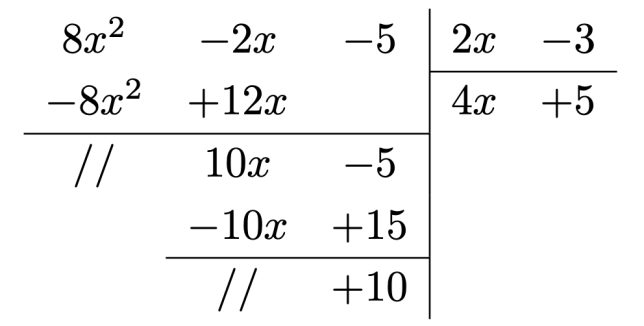


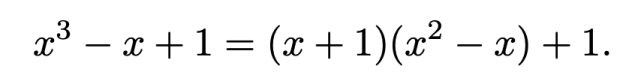





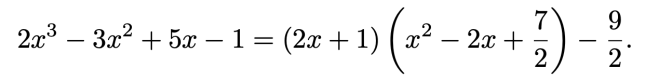







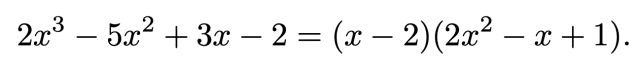










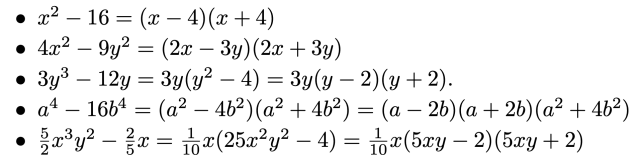





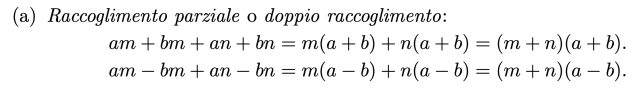




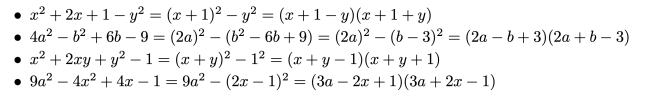



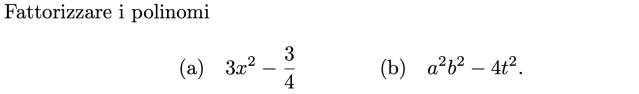




































































![{\mathbb {Q))[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/59f611a32bc84287517e9f4b283ac998c0394479)
![{\mathbb {Z))[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a538d203a057d4c604f799c28e9a7be410fdcac)












Devi effettuare l'accesso per postare un commento.