


°°°°°
In questa lezione vediamo
gli estremi vincolati,
il teorema dei moltiplicatori di Lagrange,
la funzione lagrangiana.
°°°°°
Estremi vincolati
Prima di dare la definizione cerchiamo di chiarire qual è il nostro obiettivo.
Supponiamo di avere un insieme 
e
di avere una funzione  .
.
Stiamo quindi prendendo un insieme A nel piano x y, cioè
f è una funzione in due variabili.
Poi prendiamo una curva che ha un sostegno (cioè un grafico) Γ (è la lettera “gamma” maiuscola).
L’obiettivo è capire quali sono gli estremi di f vincolata a Γ.
Γ viene detto vincolo.
La funzione f vincolata a Γ si scrive anche così: f|Γ.
In pratica
si traccia una linea verticale dopo la f e si mette il pedice Γ.
Prima di dare la definizione spieghiamo con un esempio quello che abbiamo detto.
°°°°°
esempio 1
Prendiamo la funzione seguente:

Se facciamo il test degli autovalori (Lezione 11) nel punto (0,0) notiamo che è presente un punto di sella.
Ora però ci chiediamo cosa succede se vincoliamo la funzione all’asse x.
In pratica,
vincolarla significa sostituire l’equazione dell’asse x dentro alla nostra f.
Se noi mettiamo
y=0 dentro ad f otteniamo f = x2.
Questa è la funzione vincolata all’asse x e notiamo che, essendo una parabola, ha un minimo in x=0.
La morale è che la funzione vincolata all’asse x in (0,0) ha un minimo.
Questo è un banale esempio per capire il concetto:
dobbiamo capire che cosa succede alle nostre funzioni quando le vincoliamo a determinate curve
(in questo caso all’asse x).
°°°°°
definizione: punto di massimo vincolato
Data una funzione f(x, y)
e
chiamato Γ il sostegno di una curva (contenuto nel dominio di f),
il punto (xo, yo) è un punto di massimo vincolato per f(x, y)
se esiste un intorno U di (xo, yo) tale che:

Questo significa che
la funzione nel punto di massimo deve essere più grande della funzione nei punti vicini.
Tuttavia
i punti vicini vanno presi nell’intersezione tra U e Γ
quindi non vanno presi tutti i punti
(cioè tutti quelli di U) ma solo quelli che stanno anche su Γ.
La definizione: punto di minimo vincolato
è praticamente identica,
bisogna solo mettere un “≤” al posto del “≥”.
°°°°°
metodi per individuare gli estremi vincolati
Ci sono due metodi che ci consentono di individuare gli estremi vincolati.
Vedremo un esempio
per il primo metodo (che è quello più tranquillo);
per il secondo metodo invece faremo le cose per bene.
-
Parametrizzare il vincolo
Il vincolo Γ è il sostegno di una curva. Sappiamo che le curve dipendono da un solo parametro.
Il nostro obiettivo è parametrizzare la curva, ovvero scrivere x(t) e y(t) in modo tale che poi possiamo sostituirle in f(x, y) e ottenere una funzione che dipende solo da t. A quel punto troviamo gli estremi imponendo che la derivata sia nulla (ha una variabile sola quindi è facile).
-
Usare i moltiplicatori di Lagrange
Questo metodo lo approfondiremo nel corso della lezione. Si usa una specie di teorema di Fermat, però usato per il calcolo degli estremi vincolati.
°°°°°
esempio 2:
parametrizzare il vincolo
Troviamo i massimi e i minimi della funzione f(x, y) = x y sulla circonferenza di centro (0,1) e raggio 1.
Soluzione
La circonferenza che ci danno loro è la curva, ovvero il vincolo, su cui calcolare i massimi e i minimi.
Questa circonferenza ha equazione x2 + (y-1)2 = 1 perché ha il centro in (0,1) e raggio pari a 1.
Vediamo come possiamo fare parametrizzando il vincolo.
Abbiamo detto che dobbiamo scrivere la x(t) e la y(t).
Siccome la nostra circonferenza ha centro in (0,1) otteniamo queste equazioni, che sono le tipiche equazioni di una circonferenza:

Come vedete,
noi in una circonferenza sappiamo che la x è il coseno e la y è il seno.
Se abbiamo il centro in (0,1), come y abbiamo la somma tra 1 e il seno.
Il parametro t è compreso tra 0 e 2π.
Una volta parametrizzato il vincolo basta solo sostituire le formule di x e y dentro alla nostra funzione:

Adesso
la funzione è diventata una banale g(t) quindi possiamo porre la derivata uguale a zero per calcolare gli estremi.

Dalla seconda alla terza riga abbiamo sfruttato l’equazione trigonometrica fondamentale che dice che
cos2(t) = 1 – sin2(t).
Per risolvere l’equazione poniamo sin(t) = u.
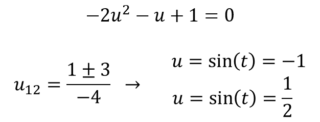
Il seno è -1 quando t = 3π/2,
mentre
Il seno è 1/2 quando t = π/6 o t = 5π/6.
Questo si capisce dalla trigonometria.
Non abbiamo messo la periodicità perché sappiamo che t ∈ [0, 2π] quindi non bisogna metterla.
Quei tre sono quindi i candidati ad essere massimi o minimi di f vincolata alla circonferenza.
Ora basta fare come in analisi 1:
guardiamo dove
la funzione cresce e decresce (cioè poniamo g'(t) > 0) e otteniamo così i massimi e i minimi.
Faremo ancora esercizi su questo quindi non aggiungo molto altro:
il concetto è che parametrizzando il vincolo riusciamo ad avere una funzione con una sola variabile e quindi utilizziamo le tecniche di analisi 1.
UNA CHICCA:
quando abbiamo trovato g'(t) possiamo direttamente porla >0 senza andare a guardare i risultati dell’equazione g'(t)=0.
°°°°°
Teorema dei moltiplicatori di Lagrange
Il teorema ci permette trovare le equazioni che ci servono per capire quali sono i punti di estremo vincolato.
Prendiamo f, g∈ C1(R2)
e
un punto di estremo vincolato P* per f sotto il vincolo Γ = {(x, y)∈ R2 t.c. g(x, y)=0}.
Se ∇ g(P*) ≠ 0
ALLORA:
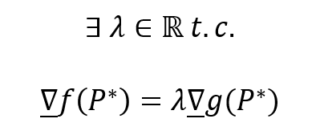
Se ∇ g(P*) = 0 allora bisogna studiare a parte quello che succede.
Il teorema ci dice che per trovare i massimi e i minimi vincolati basta risolvere il seguente sistema:
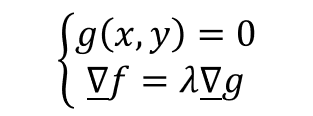
In generale,
conviene sempre cercare di parametrizzare il vincolo perché con i moltiplicatori di Lagrange si fanno un bel po’ di conti.
Ora per la vostra gioia dimostreremo il teorema.
Siccome è una dimostrazione grossa le facciamo un titoletto.
dimostrazione
Dobbiamo dimostrare che
dato un punto di estremo vincolato P*=(x*,y*) e un vincolo Γdefinito come abbiamo scritto prima, ipotizzando che il gradiente di g sia diverso da zero riusciamo a dire che esiste un λ che verifica una certa equazione (quella con i gradienti di f e g).
Organizzeremo la dimostrazione così:
-
nel primo passo dimostriamo che Γ coincide con il grafico di una funzione e quindi si può parametrizzare;
-
nel secondo passo la parametrizziamo;
-
nel terzo passo scriviamo f(x(t),y(t)) e la deriviamo perché dipende solo da t;
-
nel quarto passo dimostriamo che il gradiente di g è perpendicolare ad un certo vettore;
-
nel quinto passo concludiamo la dimostrazione.
1.- Dimostriamo che Γ si può parametrizzare.
Abbiamo detto che ipotizziamo che ∇ g(P*) ≠ 0.
Ciò significa che
una delle due derivate parziali di g è diversa da zero.
Supponiamo che sia la ∂g/∂y.
Possiamo applicare il teorema del Dini:
esiste di sicuro un’unica funzione
φ(x) tale che g(x, φ(x)) = 0 per ogni x che sta dentro ad un intorno di x*.
Siccome g(x, y)=0 era l’equazione che definiva il vincolo Γ, possiamo dire che in un intorno di x*
il vincolo si comporta come una funzione:
la x rimane x ed è la variabile indipendente mentre
la y è uguale a φ(x).
E’ quindi sicuramente parametrizzabile perché le funzioni sono sempre parametrizzabili.
2.- Scriviamo la parametrizzazione.
Definiamo una curva γ che è la parametrizzazione del vincolo Γ:

In pratica,
stiamo facendo quello che abbiamo fatto nell’esempio 2:
partiamo da un’equazione e scriviamo una curva che abbia come x e y delle funzioni dipendenti da t.
Ricordiamo che per ipotesi in P* c’è un punto di estremo vincolato sul vincolo Γ, quindi ci sarà
un punto di estremo vincolato in P* anche sul vincolo γ
perché la curva è la stessa anche se abbiamo cambiato la parametrizzazione.
3.- Deriviamo f(x(t),y(t)).
Poniamo per comodità
h(t) = f(x(t),y(t)).
Siccome quando abbiamo parametrizzato abbiamo detto che x(0)=x* e y(0)=y*,
il fatto che ci sia un punto di estremo vincolato in (x*,y*) implica che
per la funzione h(t) c’è un punto di estremo in t = 0.
In pratica,
il punto (x*,y*) = P* viene riscritto come (x(0),y(0)), che sfrutta la parametrizzazione che abbiamo fatto.
Se uno è un estremo lo sarà anche l’altro perché sono solo due modi diversi di indicare lo stesso punto.
Nel secondo caso abbiamo t = 0.
Possiamo quindi dire che per il teorema di Fermat h'(0) = 0.
Utilizzeremo questo risultato tra poco.
Ora faremo quello che in gergo tecnico si dice parkour.
Calcoliamo la h'(t) utilizzando la regola della catena
e
successivamente poniamo t = 0 in modo da trovare h'(0).
La regola della catena funziona così:
siccome h(t) = f(x(t),y(t)), deriviamo f rispetto ad x e lo moltiplichiamo per x’ e poi deriviamo f rispetto ad y e moltiplichiamo per y’.

Come vedete,
dopo aver calcolato h'(t) abbiamo posto t=0.
Siccome x(0)=x* e y(0)=y* abbiamo ottenuto la penultima riga.
Per ottenere l’ultima riga abbiamo posto
v = (x'(0), y'(0)).
Nell’ultima riga stiamo quindi facendo
un prodotto scalare tra il gradiente di f nel punto P* (che è un vettore contenente le derivate parziali di f) e il vettore v che abbiamo definito.
Siccome nel prodotto scalare facciamo
il prodotto tra la prima componente del gradiente e la prima componente di v
e
successivamente quello tra le seconde componenti,
la penultima riga e l’ultima riga sono identiche.
Vi starete chiedendo a cosa serve.
Intanto, siccome prima abbiamo detto che h'(0)=0 possiamo scrivere:

Per capire a cosa serve tutto questo dobbiamo aspettare il punto 5.
Per ora l’unica cosa che possiamo dire è che
il gradiente di f e il vettore v sono perpendicolari perché il loro prodotto scalare è nullo.
4.- Dimostriamo che ∇ g(P*) e v sono perpendicolari.
Abbiamo parametrizzato il vincolo ponendo x=x(t) e y=y(t).
Nel punto 3 abbiamo scritto f(x(t),y(t)) ma nessuno ci vieta di scrivere anche g(x(t),y(t)), tanto la parametrizzazione è valida.
Poniamo m(t) = g(x(t),y(t)).
Sappiamo dall’equazione di Γ che g(x, y)=0, quindi sarà nulla anche g(x(t),y(t)), e quindi m(t)=0.
Questo significa che se deriviamo entrambi i membri otteniamo m'(t)=0 per qualsiasi t, in particolare m'(0)=0.
Facciamo quindi la stessa cosa che abbiamo fatto nel punto 4 con la h:
calcoliamo m'(t) e poi mettiamo t = 0.

Nell’ultima riga abbiamo sfruttato il fatto che m'(0)=0.
Quindi
∇ g(P*) è perpendicolare a v.
5.- Conclusione.
Nel punto 4 abbiamo detto che
∇ f(P*) è perpendicolare a v,
mentre
nel punto 5 abbiamo detto che
∇ g(P*) è perpendicolare a v.
Quando due vettori sono perpendicolari ad uno stesso vettore significa che sono paralleli.
Ciò significa che
∇ g(P*) e ∇ f(P*) sono paralleli.
La condizione di parallelismo si indica dicendo che
un vettore è multiplo dell’altro:

Abbiamo quindi dimostrato (dopo un procedimento lungo) che
se P* è un punto di estremo vincolato su Γ allora vale la formuletta appena scritta, cioè abbiamo dimostrato
il teorema dei moltiplicatori di Lagrange.
°°°°°
Funzione Lagrangiana
Prima abbiamo detto che
per trovare gli estremi vincolati bisogna risolvere un sistema.
Il seno riassume quel sistema in un’unica (ed elegante) formula.
La lagrangiana si definisce così:
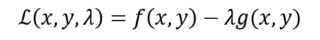
Il sistema di prima si riassume nella seguente equazione:
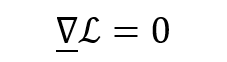
Quindi
per ottenere i punti candidati ad essere gli estremi vincolati di una funzione basta porre il gradiente della lagrangiana pari a zero
(se il gradiente di g è diverso da zero).
Concludiamo la lezione facendo vedere che
l’ultima equazione scritta corrisponde al sistema scritto nel teorema dei moltiplicatori di Lagrange:
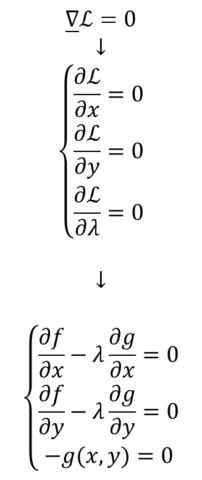
Ora dall’ultima equazione possiamo dire che g(x, y)=0
e quindi,
siccome deve esserlo sempre, dovranno essere nulle anche le sue derivate:

Quindi, come vedete,
abbiamo ottenuto il sistema che avevamo trovato nel teorema dei moltiplicatori di Lagrange.
Se vi chiedono gli estremi vincolati, dunque, fate la lagrangiana e calcolatevi il gradiente della lagrangiana. Vedremo un esempio nella prossima lezione.
Tag: Condizioni al contorno di Cauchy, Estremi vincolati, funzione lagrangiana, teorema dei moltiplicatori di Lagrange



 .
.

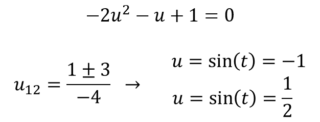







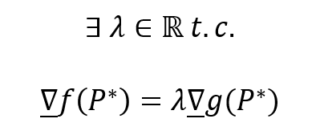
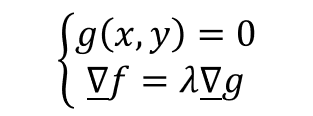



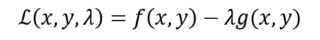
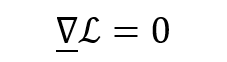
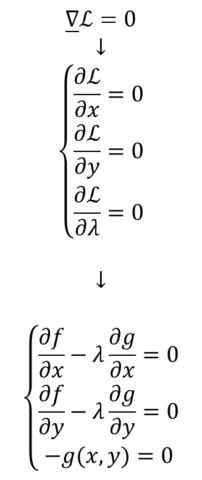


Devi effettuare l'accesso per postare un commento.