Salvatore Di Lucia
Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)
Derivata della funzione composta
Per calcolare la derivata di una funzione qualsiasi ci mancano due strumenti. In questa lezione ci occupiamo del primo: è
il teorema di derivazione della funzione composta.
Questo risultato teorico ha una grande importanza nella risoluzione degli esercizi, perché il 99% delle funzioni che dovremo derivare sono composte.
Nella lezione sull’Algebra delle derivate abbiamo visto qual è la relazione tra la derivazione e le operazioni tra funzioni;
nella tabella delle derivate notevoli, invece, abbiamo visto come calcolare le derivate delle principali funzioni mediante la definizione.
Tenetele a mente prima di proseguire nella lettura.
Indice
-
Teorema
-
Esempio
-
Con tre o più funzioni
-
Dimostrazione
Teorema per la derivata della funzione composta
Il teorema della derivata della funzione composta,
detto anche Regola di Derivazione,
stabilisce che
la derivata di una funzione composta
si calcola come prodotto tra
la derivata della funzione esterna
e
la derivata della funzione interna;
è una regola che permette di calcolare
la derivata di una composizione di funzioni
come
prodotti e derivazioni concatenate.
°°°°°
Consideriamo
due funzioni reali di variabile reale y = f(x) e z =g(y);
sia poi
z = h(x) = g(f(x)) la composizione delle due funzioni.
Supponiamo che
e che
g(y) sia derivabile in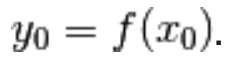 
Vale la seguente formula:
Da un punto di vista operativo,
il teorema permette di calcolare la derivata composta come funzione:
Se preferite, possiamo anche esprimere la formula come:
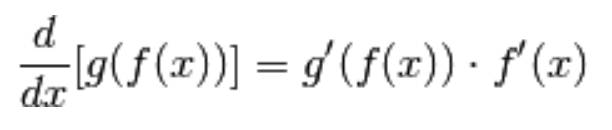
In parole povere,
la derivata della funzione composta 
è data
dalla derivata della funzione più esterna, con argomento invariato, moltiplicata per la derivata della funzione più interna.
Con “funzione più esterna”
si intende l’ultima funzione che interviene nella composizione, g(y),
con funzione “più interna”
si intende la prima funzione che si considera nella composizione, f(x).
Esempio
sulla derivazione della funzione composta
Data la funzione z = h(x), definita come:
Abbiamo
come funzione più esterna:
come funzione più interna: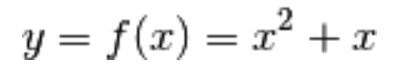
Calcoliamo le derivate separatamente.
Abbiamo
la derivata del logaritmo : 
la derivata di una somma:
Ricordiamoci che è y = f(x):
Il teorema della derivata composta ci dice che
la derivata h'(x) è data da:
°°°°°
Un modo semplice per capire
la logica della derivazione delle funzioni composte è questa:
immaginiamo che la funzione composta da derivare sia un’arancia.
Il teorema stabilisce che prima bisogna derivare la “buccia”
mantenendo la “polpa” invariata,
dopodiché si moltiplica il tutto per la derivata della “polpa”.
°°°°°
Derivazione di più funzioni composte
Il teorema si estende anche al caso di composizioni di tre o più funzioni.
Ad esempio,
nel caso di tre funzioni p(x), q(x), r(x) :
h(x) = r(q(p(x))) ; → h'(x) = r'(q(p(x)))·q'(p(x))·p'(x)
Si procede allo stesso modo nel caso di n funzioni composte tra loro:
si parte derivando la funzione più esterna
(l’ultima in ordine di composizione)
e se ne mantiene l’argomento invariato.
Poi, si passa al livello successivo:
si dimentica la funzione appena derivata,
si deriva la funzione successiva e se ne mantiene l’argomento invariato.
Si moltiplicano tutte le derivate ottenute e si procede così fino alla funzione più interna, ossia la prima in ordine di composizione.
Esempio
Deriviamo la seguente funzione:
Notiamo che
h(x) è la composizione di tre funzioni, h(x) = r(q(p(x))), dove:
Calcoliamo le tre derivate separatamente
(ricordando qual è la derivata del seno):
Applichiamo il teorema:
Nota bene
Quando in una composizione di funzioni ci si riferisce
all’ultima funzione in ordine di composizione
si intende la prima funzione che si scrive.
Ad esempio,
in f(x) = Z(W(…(A(X))))
l’ultima funzione in ordine di composizione è Z, è la prima da derivare.
La prima funzione in ordine di composizione è A, è l’ultima da derivare.
Dimostrazione
del teorema di derivazione della funzione composta
Diamo la dimostrazione nel caso di due funzioni,
siano z = g(y) e y = f(x),
cosicché
la funzione composta è z = h(x) = g(f(x)).
Nel caso di più funzioni composte si ragiona in modo analogo.
Usiamo la definizione di derivata
e
calcoliamo il limite del rapporto incrementale in 
per la funzione h(x).
Obiettivo:
provare che
il limite esiste finito e che si calcola con la formula dell’enunciato.
Scriviamo espressamente h(x) come funzione composta:
moltiplichiamo e dividiamo la frazione per 
.
Ora ricordiamo che f(x) = y e che 
Inoltre è chiaro che al tendere di 
anche 
ossia che 
Questo perché
la funzione f è derivabile in ,
e
in quanto tale è anche ivi continua.
Grazie a queste considerazioni,
e a una semplice regola dell’Algebra dei limiti:
(il limite di un prodotto é uguale al prodotto dei limiti)
possiamo calcolare:
La funzione g(y) è derivabile in 
per ipotesi,
dunque
il primo limite esiste e vale 
discorso analogo
per f(x), che è derivabile in .
il secondo limite esiste e vale
Ricordiamo infine che 
, e la dimostrazione è conclusa.
Anche se all’inizio la tecnica di derivazione della funzione composta può apparire impegnativa, dopo una pò di esercizi risulta molto più semplice.
°°°°°
Tag: Derivata della funzione composta
Salvatore Di Lucia
Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)
Calcolo delle derivate: regole di derivazione
Se si conoscono le derivate delle funzioni elementari,
l’Algebra delle derivate è la base che permette di calcolare
la derivata di una qualsiasi funzione
in cui sono presenti
somme e differenze, prodotti e rapporti di funzioni.
Per l’elevamento a potenza ci servirà invece
il teorema per la derivata della funzione composta,
di cui parleremo nella prossima lezione;
per la funzione inversa ci servirà invece
il teorema per la derivata della funzione inversa.
Indice
1.) Regole di derivazione
2.) Esempi
1.) Regole di derivazione per il calcolo delle derivate
Il calcolo delle derivate è un procedimento che si basa su un insieme di regole,
dette
regole di derivazione,
che descrivono il comportamento della derivazione rispetto alle operazioni algebriche tra funzioni:
prodotto per una costante,
somma e differenza,
prodotto e rapporto.
Ognuna delle seguenti regole si dimostra usando
la definizione di derivata.
1.) La derivata del prodotto di una costante per una funzione
è uguale
alla costante per la derivata della funzione.
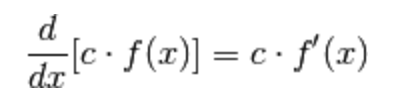
Ogni volta che abbiamo un coefficiente che moltiplica una funzione,
se dobbiamo derivare il tutto,
basta riscrivere il coefficiente e derivare solamente la funzione.
2.) La derivata di una somma o differenza di funzioni
è uguale
alla somma o differenza delle singole derivate.
Dunque se dobbiamo derivare una somma o una differenza di funzioni,
ci basterà derivare i singoli addendi.
Vi facciamo notare che la regola fa riferimento alla somma algebrica,
intesa quindi come addizione o sottrazione.
Si procede in modo analogo nel caso della somma o differenza di tre o più funzioni.
3.) La derivata del prodotto di due funzioni
è uguale
alla prima funzione derivata per la seconda più la prima funzione per la derivata della seconda.
Nel caso del prodotto di tre o più funzioni vale una regola analoga, che si ottiene considerando due fattori come un’unica funzione e reiterando la formula.
Per approfondire:
°°°°°
4.) La derivata del rapporto di due funzioni
è uguale
al rapporto tra la derivata del numeratore per il denominatore
meno il numeratore per la derivata del denominatore,
tutto fratto il denominatore al quadrato.
Per approfondire:
°°°°°
Per i più esperti che stanno leggendo questo articolo,
le prime due regole si riassumono dicendo che
l’operatore di derivazione D : f → f’ è lineare e omogeneo.
°°°°°
Esempi di calcolo delle derivate
Prima di procedere è bene sapere quali sono
le derivate fondamentali,
perlomeno per le funzioni più ricorrenti.
1.) Data la funzione
per la regola di derivazione del prodotto costante-funzione abbiamo che:
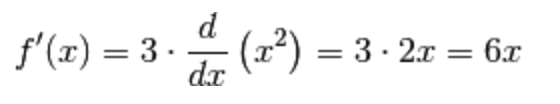
2.) Data la funzione
dalla regola di derivazione della differenza di funzioni risulta:
3.) Data la funzione
per la regola di derivazione del prodotto di funzioni:
4.) Data la funzione
per la regola di derivazione del rapporto di funzioni risulta:
Qui basta ricordare le espressioni per la derivata di una potenza e per la derivata del coseno:
°°°°°
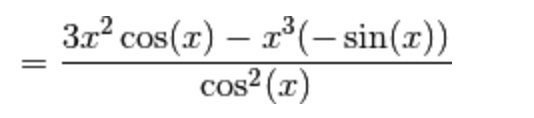
Esempio misto con applicazione di più regole
Vediamo un esempio in cui dobbiamo applicare più regole di derivazione. Consideriamo la seguente funzione e calcoliamone la derivata.
1.) 
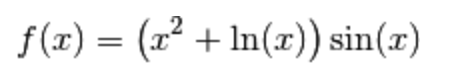
In accordo con le regole sull’ordine delle operazioni prima si effettuano i prodotti e poi le somme, quindi prima di tutto applichiamo la regola di derivazione del prodotto:
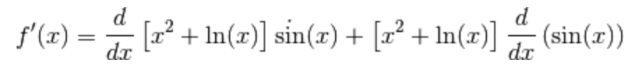
Al primo addendo applichiamo la regola di derivazione della somma di funzioni:
Infine, grazie alla tabella delle derivate delle funzioni elementari:
L’aspetto importante dell’esempio riguarda
l’ordine da seguire nei vari livelli di derivazione:
è lo stesso delle operazioni algebriche.
Per essere in grado di calcolare qualsiasi derivata ci mancano
i teoremi di derivazione della funzione composta e dell’inversa.
°°°°°
Tag: Calcolo delle derivate: regole di derivazione
Salvatore Di Lucia
Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)
Derivate fondamentali:
tabella e dimostrazioni
Le derivate fondamentali, o derivate notevoli, sono le derivate delle funzioni elementari e delle funzioni più ricorrenti:
vengono ricavate con la definizione, una volta per tutte, e successivamente utilizzate nei calcoli dandole per buone.
In questa lezione elenchiamo tutte le derivate notevoli.
Se state pensando che dovrete saperle a memoria… Avete ragione!
Ma niente paura:
sarà sufficiente fare un po’ di esercizi per ricordarle automaticamente.
Dunque, vi sconsigliamo di impararle come se si trattasse di una poesia:
studiate le dimostrazioni e usatele di volta in volta negli esercizi.
Il resto verrà da sé.
Conoscere le derivate fondamentali è molto utile
perché,
insieme all’Algebra delle derivate
ai teoremi di derivazione che studieremo nelle lezioni successive,
ci permetteranno di calcolare velocemente
la derivata di una qualsiasi funzione y = f(x).
Tabella delle derivate fondamentali
A seconda dei contesti le derivate fondamentali possono riferirsi a:
1.) le derivate delle funzioni elementari,
che vengono dimostrate mediante la definizione di derivata;
2.) le derivate delle funzioni più ricorrenti, tra cui le funzioni elementari e non solo.
In tabella elenchiamo le funzioni, le relative derivate e il link alle rispettive dimostrazioni.
I.) Con [DEF] indichiamo quelle che si dimostrano con la definizione;
II.) con [AD] quelle che si calcolano con l’Algebra delle derivate
III.) con [DFI] quelle che si ricavano con il teorema di derivazione della funzione inversa.
Se state seguendo le lezioni nel loro ordine, sappiate che affronteremo
l’Algebra delle derivate
il teorema per la derivata dell’inversa nelle lezioni successive.
Derivate ricorrenti ma non fondamentali
Le derivate
Grafico:
°°°°°
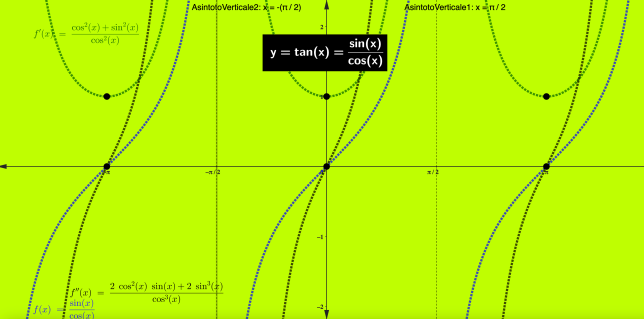
Grafico:
°°°°°
Grafico:
°°°°°
Grafico:
°°°°°
Grafico:
°°°°°
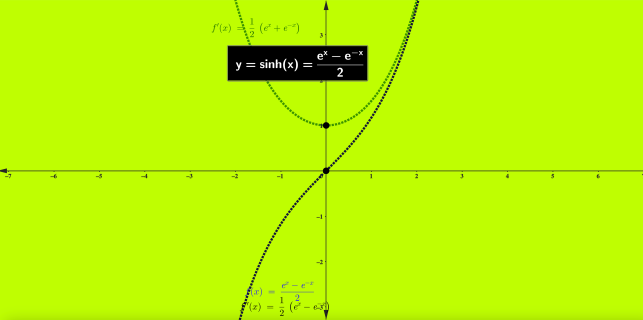
Grafico:
°°°°°
della tangente iperbolica: 
Grafico:
°°°°°
della cotangente iperbolica: 
Grafico:
sono elencate per completezza ma
non sono propriamente derivate fondamentali,
perché si possono ricavare dalle altre con l’Algebra delle derivate.
°°°°°
Un discorso analogo vale per le derivate
della funzione arcoseno:
Grafico:
della funzione arcocoseno:
Grafico:
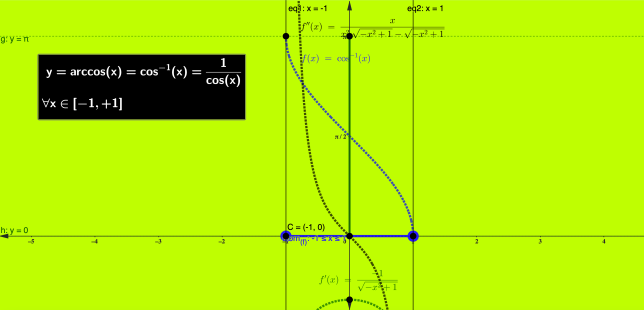
della funzione arcotangente:
Grafico:
della funzione arcocotangente :
Grafico:
perché il modo più semplice per calcolarle si basa sul
teorema di derivazione della funzione inversa.
°°°°°
Derivate di radici e di funzioni fratte
In tabella non abbiamo elencato le derivate
delle funzioni radici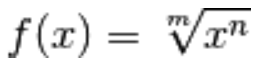 
né delle funzioni fratte
con n∈N,
perché ricordarle a memoria è inutile.
Ad esempio,
per derivare una radice della forma
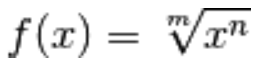
basta riscriverla secondo la definizione di radicale,
come potenza con esponente fratto:
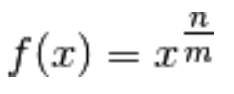
Quindi, grazie alla derivata della potenza indicata in tabella:
Se invece dovessimo derivare il reciproco di una potenza come
sarebbe sufficiente riscriverla come potenza ad esponente negativo
e usare la derivata della potenza:
°°°°°
Alcune dimostrazioni delle derivate fondamentali
Vediamo le dimostrazioni di alcune derivate notevoli con la definizione,
in estrema sintesi e a titolo esemplificativo.
Sappiate che in generale sono semplici e vanno sapute;
se volete approfondire i passaggi,
come pure leggere quelle che non menzioniamo qui,
potete fare riferimento alle pagine linkate in tabella.
Come anticipato,
le derivate delle funzioni elementari si deducono applicando la definizione.
Dovremo sempre calcolare
il limite del rapporto incrementale in un generico punto x.
Spesso dovremo usare uno dei limiti notevoli per portare a termine il calcolo, e attenzione:
qui è h che tende a zero, non x.
°°°°°
1.) Se f(x) è costante,
allora
f'(x) = 0.
°°°°°
2.) Se f(x) = x,
allora
f'(x) = 1.
°°°°°
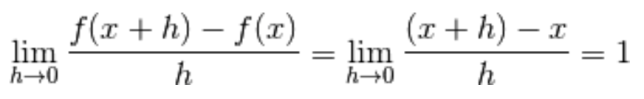
3.) Se 
allora
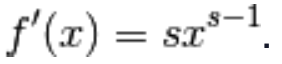
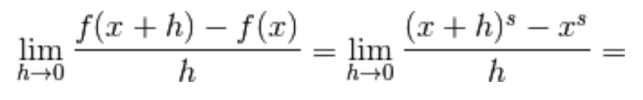
Raccogliamo la x tra parentesi:
Raccogliamo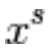 
a numeratore:
Dividiamo e moltiplichiamo per x a denominatore
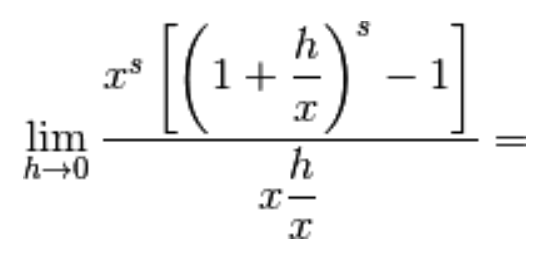
e infine applichiamo il limite notevole:
°°°°°
4.) Se 
allora
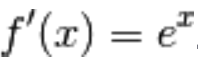
Raccogliamo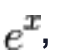 
e per una nota proprietà delle potenze:
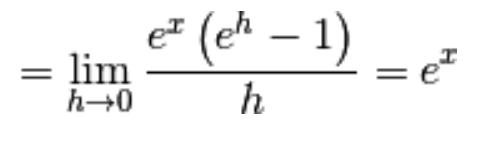
Nell’ultimo passaggio abbiamo usato il limite notevole dell’esponenziale.
Si ragiona in modo analogo
°°°°°
5.) se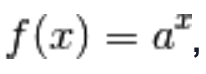 
,
per cui troviamo 
.
°°°°°
6.) Se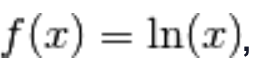 
allora
Per una nota proprietà dei logaritmi,
il logaritmo di un rapporto è la differenza dei logaritmi, e viceversa:
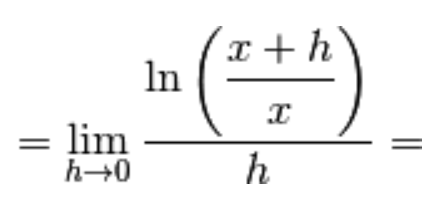
Dividiamo termine a termine nell’argomento del logaritmo:
Dividiamo e moltiplichiamo per x a denominatore
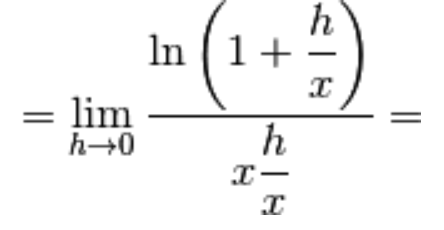
e applichiamo il limite notevole del logaritmo:
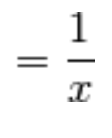
In modo analogo
°°°°°
7.) se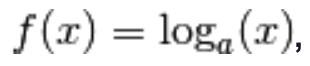 
allora
°°°°°
8.) Se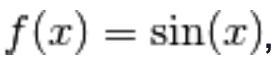 
allora
Usiamo la formula di addizione degli angoli per il seno:
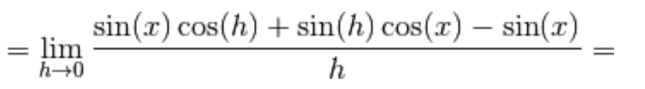
Spezziamo il limite in modo opportuno:
Ora, per h → 0 risulta che cos(h) → 1, quindi il primo limite vale zero.
Sul secondo limite applichiamo il limite notevole del seno:
In modo analogo si prova che
°°°°°
9.) se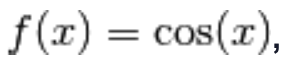 
allora
°°°°°
Tag: Derivate fondamentali
Salvatore Di Lucia
Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)
Relazione tra continuità e derivabilità
In una delle precedenti lezioni abbiamo trattato
la condizione necessaria e sufficiente per la derivabilità
di una funzione reale di variabile reale y =f(x) in un punto 
del suo dominio.
Ora vogliamo studiare qual è
il legame tra derivabilità e continuità in un punto:
1.) si implicano a vicenda?
2.) Oppure una delle due implica l’altra?
3.) O ancora: non c’è alcuna relazione?
Se avete presente la definizione di continuità di una funzione in un punto allora potete procedere con la lettura; in caso contrario vi raccomandiamo un ripasso tattico. 😉
Indice
-
Relazione
Rapporto tra continuità e derivabilità
La relazione tra continuità e derivabilità è un legame teorico,
di semplice dimostrazione, secondo cui
la continuità è condizione necessaria ma non sufficiente per la derivabilità,
mentre
la derivabilità è condizione sufficiente ma non necessaria per la continuità.
Che cosa significano le espressioni “condizione necessaria” e “condizione sufficiente”?
Lo spieghiamo in un’apposita lezione: eventualmente prendetevi cinque minuti per togliervi il dubbio una volta per tutte, e poi proseguite.
Analizziamo ciò che abbiamo scritto punto per punto.
La continuità è condizione necessaria, ma non sufficiente, per la derivabilità:
una funzione deve essere continua per essere derivabile,
ma
la continuità di per sé non garantisce la derivabilità.
La derivabilità è condizione sufficiente, ma non necessaria, per la continuità:
una funzione derivabile è sicuramente continua,
ma
una funzione non derivabile potrebbe comunque essere continua.
Esplicitamente
-
se una funzione è continua in un punto allora potrebbe essere derivabile nel punto;
-
se una funzione non è continua in un punto, è certamente non derivabile nel punto;
-
se una funzione è derivabile in un punto, è sicuramente continua nel punto;
-
se una funzione non è derivabile in un punto, potrebbe comunque essere continua nel punto.
Analizziamo
la relazione tra continuità e derivabilità in termini più formali.
Teorema:
una funzione derivabile in un punto è continua nel punto
Enunciato:
sia y = f(x)
e
sia 
.
Supponiamo che f sia derivabile in .
Allora
la funzione f è continua nel punto .
Sintesi:
la derivabilità è condizione sufficiente per la continuità;
ciò equivale a dire che
la continuità è condizione necessaria per la derivabilità,
perché
se sussiste la derivabilità deve necessariamente sussistere la continuità.
Dimostrazione:
vogliamo provare che una funzione y=f(x) derivabile in un punto
è continua in ,
ossia che:
In modo equivalente:
Consideriamo la seguente uguaglianza per 
:
Riscriviamola nella forma:
Passiamo al limite per h→0 in entrambi i membri:
Grazie all’algebra dei limiti possiamo spezzare il limite della somma nella somma dei limiti:
Il primo limite a destra è il limite di una costante; il secondo limite si può riscrivere come prodotto di due limiti:
Essendo la funzione derivabile in 
, il limite del rapporto incrementale esiste finito e il suo valore è per definizione la derivata della funzione nel punto. Ciò esclude potenziali forme di indeterminazione del tipo ![[∞·0]](image/gif;base64,R0lGODlhMAASAOMAAP///wAAACIiIjAwMIqKip6enhYWFgQEBFBQULa2tkBAQGJiYgwMDObm5nR0dMzMzCH5BAEAAAAALAAAAAAwABIAAATGEAAxiLw4682zG4MUdmSJEYuzFNg4mvBWCJeRXG6sZ4IlfTjRbggI3CSFQxDwAhQMhwMCkxgoEAvdI/C4JAINIdM7BSQYjLBDcWlkYd+uJC5+lSWNA4PQBBDCVAxHXlyEcjk/GV9gGQ0+XgcsGFuDBYxjmAAOGgoBd3iPJQGSfkp1F29eAggBoQRyJgKbEgsviE6kCQJhnT4JnyUzNbC3flgDnw4MBwZsOygECKSYfQCAGtdEG8Xa3dTe4N/h3SMUoeMmHwMRADs=)
e garantisce la validità dell’uguaglianza.
In conclusione:
da cui la continuità della funzione nel punto .
°°°°°
Controesempio:
continuità come condizione non sufficiente per la derivabilità
Non abbiamo ancora dimostrato che
la continuità non garantisce la derivabilità (“non sufficiente“);
in modo analogo, che in assenza
di derivabilità può comunque esserci continuità (“non necessaria“).
Per provarlo
consideriamo un controesempio di
funzione continua ma non derivabile in un punto:
la funzione valore assoluto f(x) = |x| è continua in 
ma
non è derivabile in .
La continuità
si deduce osservando che i due limiti sinistro e destro, per 
, coincidono con la valutazione della funzione nel punto .
La derivabilità in
consideriamo i due limiti sinistro e destro del rapporto incrementale:
se sono finiti e uguali, allora la funzione è derivabile nel punto,
in caso contrario non lo è.
In particolare
è un punto angoloso per f(x) = |x|.
Nella prossima lezione ci occupiamo finalmente delle
derivate di funzioni elementari,
ossia
il punto di partenza per imparare a calcolare a mano la derivata di una qualsiasi funzione.
°°°°°
Tag: Relazione tra continuità e derivabilità
Salvatore Di Lucia
Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)
Punti di non derivabilità
1.) punto angoloso,
2.) punto di cuspide,
3.) punto di flesso a tangente verticale.
Dopo aver studiato la definizione di derivata e la condizione di derivabilità di una funzione in un punto, vediamo in che modo
una funzione può essere non derivabile in un punto.
In questa lezione cataloghiamo i vari tipi di punti di non derivabilità,
proponiamo alcuni esempi ,
alcuni suggerimenti per riconoscerli e non fare confusione.
Indice
-
Definizione e classificazione
-
Punto angoloso
-
Cuspide
-
Flesso a tangente verticale
-
Casi particolari
-
Metodo
Tipi di punti di non derivabilità
I punti di non derivabilità di una funzione sono i punti del dominio in cui la derivata prima non è definita,
e possono essere di tre tipi:
1.) punto angoloso,
2.) punto di cuspide,
3.) punto di flesso a tangente verticale.
Nella lezione sulla condizione di derivabilità abbiamo visto
sotto quale condizione una funzione reale di variabile reale è derivabile in un punto.
In sintesi:
quando esiste la derivata di una funzione in un punto.
Ricordiamo che
una funzione y = f(x) è derivabile in un punto 
del suo dominio
se
il limite sinistro e il limite destro del rapporto incrementale
esistono finiti e uguali.
Se
non sussiste anche solo una delle precedenti condizioni
– finiti e uguali –
la funzione f non è derivabile nel punto 
Indicativamente possiamo avere uno dei seguenti tipi di
punti di non derivabilità:
-
punto angoloso
-
punto di cuspide
-
punto di flesso a tangente verticale
Vediamo
quali condizioni caratterizzano i possibili punti di non derivabilità.
1.) Punto angoloso
Una funzione y = f(x) non è derivabile in
e presenta un punto angoloso
se
il limite sinistro e il limite destro del rapporto incrementale
esistono entrambi finiti, ma assumono valori diversi.
Esempio
Il più classico degli esempi:
la funzione valore assoluto f(x) = |x| presenta in 
un punto angoloso,
infatti:
Commento
Questo tipo di punto di non derivabilità è tipico
delle funzioni con uno o più valori assoluti,
e
delle funzioni definite a tratti
ossia
quelle funzioni che sono definite da rami diversi, ciascuno su un sottoinsieme del dominio.
Per quanto riguarda l’interpretazione geometrica, il nome non tradisce l’aspetto:
in un punto angoloso
il grafico della funzione forma infatti un vero e proprio angolo.
Ad esempio,
nel caso della funzione modulo di x , f(x) = |x| abbiamo la situazione rappresentata in figura.
2.) Punto di cuspide
Una funzione y = f(x) non è derivabile in
e presenta un punto di cuspide
Se
il limite sinistro e il limite destro del rapporto incrementale
sono infiniti,
e in particolare
infiniti di segno opposto,
allora
la funzione y = f(x) presenta in un punto di cuspide.
Ci sono due possibilità:
Esempio
Consideriamo
la funzione 
, che presenta in
un punto di non derivabilità.
Infatti:
(Dubbi sul calcolo dei precedenti limiti? Si tratta di un semplice confronto tra infiniti).
Commento
I punti di non derivabilità del tipo cuspide
si presentano tipicamente in presenza di radici ad indice pari.
In termini grafici
un punto di cuspide è un punto in cui
la funzione cresce con pendenza infinita
(verticalmente)
in uno dei due intorni sinistro o destro del punto,
e
la funzione decresce con pendenza infinita nell’altro intorno
(sinistro o destro).
Un’immagine vale più di mille parole:
ecco il grafico di .
3.) Punto di flesso a tangente verticale
Una funzione y = f(x) non è derivabile in
e presenta un punto di flesso a tangente verticale
Se
il limite sinistro e il limite destro del rapporto incrementale
della funzione y = f(x) sono infiniti dello stesso segno,
allora
è un punto di flesso a tangente verticale.
Anche in questo caso abbiamo due possibilità:
Esempio
L’esempio standard che si considera nel caso dei
punti di flesso a tangente verticale è la radice cubica di x: 
Lasciamo a voi il compito di verificare che in questa funzione ha
il limite sinistro e il limite destro del rapporto incrementale
che valgono più infinito.
Commento
Come si può vedere nel grafico di ,
un punto di flesso a tangente verticale è
un punto di flesso nell’intorno del quale la funzione cresce con pendenza infinita sia a sinistra che a destra del punto.
L’alternativa è che
nell’intorno del punto la funzione decresca con pendenza infinita sia a sinistra che a destra del punto.
I flessi a tangente verticale sono tipici delle radici ad indice dispari.
Casi particolari di punti di non derivabilità
Abbiamo una classificazione generale dei punti di non derivabilità, e ci domandiamo:
è esaustiva e copre tutti i casi possibili?
No, ma non allarmatevi.
Le possibilità che possono manifestarsi in astratto non possono essere racchiuse in un semplice elenco, ma non importa.
Noi abbiamo una definizione di funzione derivabile in un punto e, alla peggio, di derivabilità da destra o da sinistra nel caso delle funzioni con estremi finiti del dominio.
Se la condizione di derivabilità è soddisfatta,
allora la funzione è derivabile nel punto considerato;
se la funzione non soddisfa la condizione di derivabilità,
il punto potrebbe rientrare in uno dei precedenti casi
(punto angoloso, cuspide, flesso a tangente verticale)
oppure no.
Come classifichiamo un punto di non derivabilità
che non rientra nei tre casi principali?
Semplice:
non lo classifichiamo perché non sarebbe utile farlo;
ci limitiamo a dire che si tratta di un punto di non derivabilità.
Oltre ai tre casi notevoli i possibili casi particolari sono troppo numerosi e, ancor peggio, ci sono troppi nomi che dipendono dalla letteratura di riferimento.
Ad esempio,
se avessimo un punto tale per cui:
alcuni lo chiamerebbero semicuspide ed altri punto angoloso.
Noi ci limiteremmo a chiamarlo punto di non derivabilità.
Anche per quanto riguarda gli estremi finiti del dominio, ossia
quelli in cui possiamo studiare solo la derivabilità da sinistra o da destra come nel caso delle funzioni 
, non ha senso dare definizioni particolari.
Per noi
x = a può essere un punto di derivabilità da destra o di non derivabilità,
x = b può essere un punto di derivabilità da sinistra o di non derivabilità.
In alcuni casi vengono chiamati punti di arresto, in altri non hanno un nome specifico.
Come individuare i punti di non derivabilità
Per concludere veniamo al dubbio che qualunque studente si è posto almeno una volta nella vita.
Data una funzione di cui dobbiamo studiare la derivabilità,
come facciamo a capire
in quali punti essa potrebbe non essere derivabile
senza avere in partenza dei punti di riferimento da analizzare?
Innanzitutto vogliamo rassicurarvi:
si tratta di un compito piuttosto semplice, in generale, e l’esperienza vi aiuterà molto.
Per arrivare ad avere l’esperienza necessaria, però, è bene disporre di un metodo di partenza.
La serie di indicazioni che stiamo per fornirvi risolve il 99% degli esercizi,
sia alle Superiori che all’Università.
Il restante 1% racchiude casi patologici che si affrontano solo negli studi più avanzati e che sapreste come gestire, se vi riguardassero.
L’idea è isolare
i possibili punti di non derivabilità per esclusione,
e condurre su ciascuno di essi uno studio approfondito mediante la definizione.
1.) Tenete sempre a mente il comportamento delle funzioni elementari.
2.) Dai teoremi visti nella lezione sulla definizione di funzione derivabile sappiamo che
somma, differenza, prodotto, quoziente, composizione di funzioni derivabili sono derivabili.
Ciò ci permette di limitare parecchio i potenziali punti di non derivabilità.
3.) Detta f la funzione in esame, individuiamo il dominio Dom(f).
4.) Calcoliamo la derivata della funzione f’
(se non sapete come fare, tranquilli: ce ne occupiamo nelle lezioni successive)
e determiniamone il dominio Dom(f’) .
5.) A scanso di equivoci, intendendo f’ come funzione a sé stante,
consideriamo
i punti che appartengono a Dom(f) e che non appartengono a Dom(f’) .
Ricordiamo che
nei punti in cui f non è definita non ha senso parlare di derivabilità.
6.) Nei punti in cui le funzioni f e f’ sono continue non abbiamo alcun problema,
perché
la condizione di derivabilità è necessariamente soddisfatta
quelli in cui f’ non è continua potrebbero rivelare qualche sorpresa.
7.) Se abbiamo a che fare con una funzione definita a tratti, a prescindere da tutte le precedenti considerazioni, il punto di raccordo x = b richiede sempre un’analisi attenta.
8.) Se la funzione in esame non è patologica,
i punti che abbiamo isolato nei precedenti passaggi sono
possibili punti di non derivabilità.
Procediamo quindi con
il calcolo dei limiti sinistro e destro del rapporto incrementale.
°°°°°
Tag: Punti di non derivabilità
iMathematica 
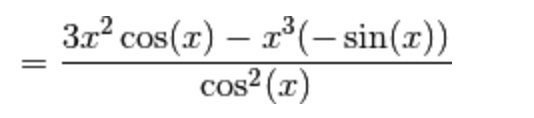
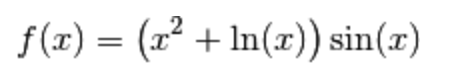
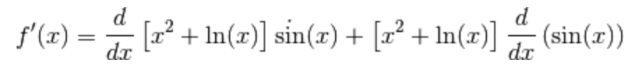
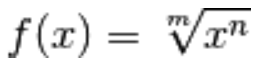
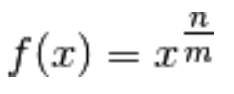
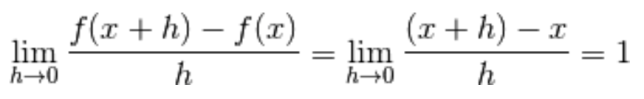
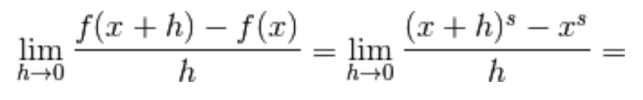
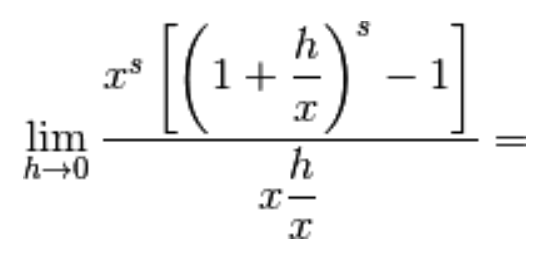
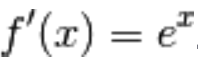
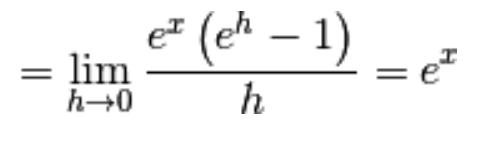
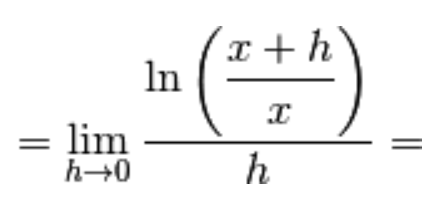
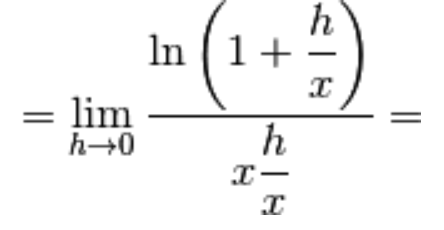
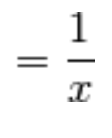
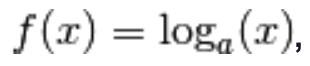
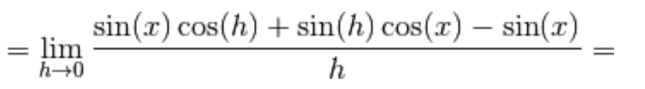
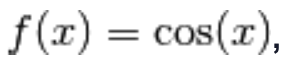
Devi effettuare l'accesso per postare un commento.