Salvatore Di Lucia
Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)
Derivata della funzione inversa
Ora che conosciamo
il primo dei due teoremi fondamentali sul calcolo delle derivate
(derivata della funzione composta),
passiamo a studiare il secondo:
il teorema di derivazione della funzione inversa.
Per capire il significato e l’utilità del teorema è necessario avere un’idea chiara su cos’è l’inversa di una funzione.
In questa lezione ne diamo un cenno, ma in caso di dubbi vi invitiamo a leggere la lezione di riferimento: inversa di una funzione.
Indice :
-
Premessa
-
Teorema
-
Esempio
-
Dimostrazione
°°°°°
1.) Premessa: a proposito della funzione inversa
Sia
y = f(x) una funzione reale di variabile reale con dominio Dom(f),
e supponiamo che
y = f(x) sia biunivoca, ossia iniettiva e suriettiva.
Allora
esiste una funzione inversa,
vale a dire
una funzione x = g(y) tale che g(f(x)) = x.
L’inversa di una funzione f si indica con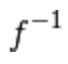 
e stabilisce proprio
la corrispondenza inversa rispetto all’associazione definita da y = f(x),
in modo che
la composizione delle due funzioni si riduca alla funzione identità su Dom(f),
ossia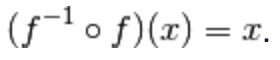 
°°°°°
2.) Teorema di derivazione della funzione inversa
Il teorema per la derivata della funzione inversa è un risultato teorico
che permette di
calcolare la derivata dell’inversa di una funzione in un punto
senza
conoscere l’espressione analitica dell’inversa.
Enunciato.
Consideriamo
una funzione y=f(x) invertibile, derivabile in un punto 
e
supponiamo che
f(x) abbia derivata diversa da zero nel punto: 
Allora
la funzione inversa 
è derivabile nel punto 
e la sua derivata in tale punto è: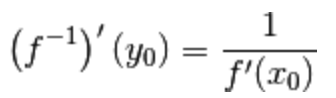
L’enunciato può sembrare difficile,
ma analizzandolo si vede subito che non lo è.
Per ipotesi la funzione f deve essere invertibile,
dunque tale da ammettere una funzione inversa ;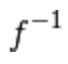
deve essere derivabile in un punto del suo dominio e
la derivata in tale punto deve essere diversa da zero: .
Sotto queste condizioni, la tesi fornisce due informazioni:
I.) la funzione inversa 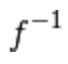è derivabile nell’immagine del punto mediante f, ossia in 
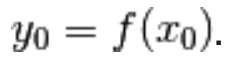
II.) sappiamo anche come
calcolare la derivata della funzione inversa 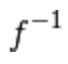nel punto 
,
ossia come
reciproco della derivata della funzione f nel punto .
Qualcuno potrebbe confondersi leggendo le parole tra simboli e punti, ma la seguente immagine dovrebbe chiarire le idee.
Per quale motivo il teorema è utile?
Perché
ci permette di calcolare la derivata di una funzione – l’inversa – senza bisogno di derivarla.
Inoltre,
nonostante il teorema fornisca un criterio di calcolo della derivata dell’inversa in un punto,
possiamo conoscere in automatico la derivata dell’inversa come funzione:
è sufficiente applicare la formula del teorema considerando un punto generico.
Esempio
di derivazione della funzione inversa
Se siete interessati a esempi numerici, al termine della lezione vi suggeriamo di leggere la scheda correlata di esercizi risolti.
Qui vediamo un esempio un po’ più fine,
utile per mostrare l’importanza del teorema.
3.) Esempio:
usare il Teorema di derivazione della funzione inversa per dimostrare che
Svolgimento:
consideriamo la funzione logaritmica f(x) = ln (x), e non a caso.
Il suo dominio è Dom (f) = (0,+∞),
è biunivoca,
è derivabile su tutto il suo dominio.
Conosciamo la funzione inversa della funzione logaritmica,
che è proprio l’esponenziale: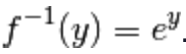 
.
Infatti:
Sappiamo che la derivata del logaritmo è:
Usiamo il teorema di derivazione della funzione inversa,
considerando come un generico punto.
Possiamo farlo perché la derivata f'(x) non si annulla in alcun punto del dominio, quindi le ipotesi del teorema sono soddisfatte.
La tesi ci dice che
la derivata dell’inversa nel punto
è il reciproco della derivata 
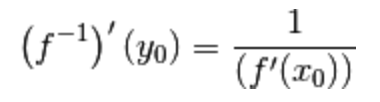
Poiché è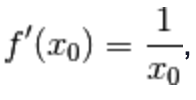 
, sostituiamolo nell’uguaglianza:
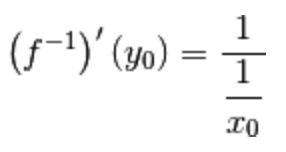
Poiché è 
, possiamo scrivere:
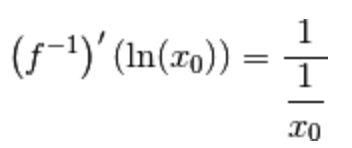
A destra dell’uguale possiamo usare la regola per le frazioni di frazioni:
Cosa abbiamo scoperto?
Che
è quella funzione che, applicata al logaritmo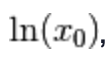 
, dà .
Quindi,
per la generalità del punto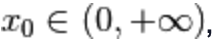 
, abbiamo scoperto che anchedeve comportarsi come inversa della funzione ln (x).
In sintesi:
il teorema ci ha permesso di calcolare
la derivata dell’inversa di f(x) = ln (x),
ossia
la derivata della funzione esponenziale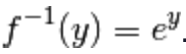
Questa derivata deve comportarsi come inversa del logaritmo,
quindi deve essere a sua volta l’esponenziale:
E abbiamo trovato che
la derivata dell’esponenziale è l’esponenziale stessa.
°°°°°
4.) Dimostrazione
del teorema per la derivata della funzione inversa
Concludiamo con la dimostrazione del teorema.
Dato che vogliamo ricavare
la formula per la derivata dell’inversa in un punto, facciamo riferimento
alla definizione di derivata come limite del rapporto incrementale.
Per ipotesi
la funzione inversa 
esiste,
perché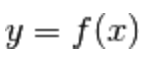 
è invertibile.
Consideriamo il limite del rapporto incrementale della funzione inversa centrato nel punto
Quest’ultimo è l’immagine di un punto in cui la funzione 
è derivabile con derivata diversa da zero: .
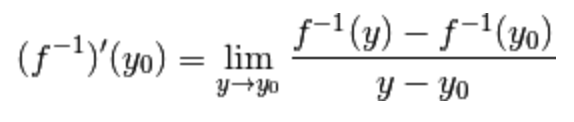
Vogliamo
dimostrare che questo limite esiste finito e che è uguale al reciproco di .
Riscriviamolo esprimendo tutto nella variabile x, ma facciamolo con cautela.
Dire che 
significa che 
: ciò implica che 
?
Sì, perché f(x) è una funzione derivabile in ,
dunque è anche continua in .
Dai teoremi sulla continuità anche
l’inversa deve essere continua nell’immagine ,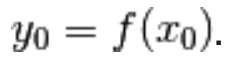
ossia
al tendere di risulta che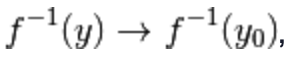 
,
e questo significa che .
Possiamo allora riscrivere
il limite del rapporto incrementale
come:
Per definizione di funzione inversa,
risulta che
e che
.
Ciò ci permette di esprimere
il limite del rapporto incrementale
nel seguente modo:
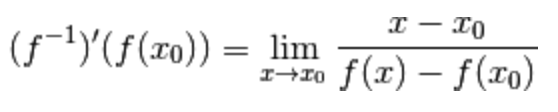
Osserviamo attentamente il limite appena scritto.
Esso non è altro che il reciproco del rapporto incrementale associato alla funzione f(x) e centrato in :
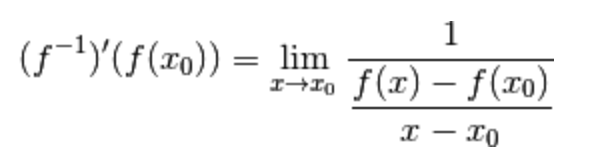
Per ipotesi la funzione f(x) è derivabile in ,
dunque esiste ed è finito il limite:
A questo punto facciamo intervenire l’Algebra dei limiti
e l’ipotesi per cui , così che esiste finito il limite:
Di conseguenza
la funzione 
è derivabile in ,
e la derivata in tale punto vale:
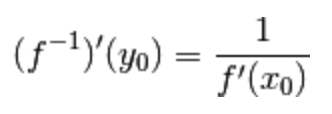
Ossia la tesi.
Nella scheda correlata di esercizi svolti ci concentriamo sull’applicazione pratica del teorema, ossia come calcolare la derivata della funzione inversa in uno specifico punto.
°°°°°
iMathematica 
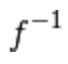
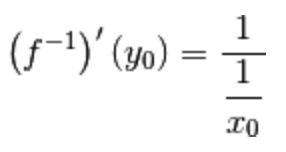
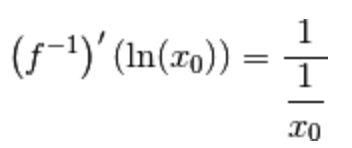
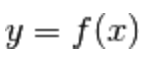
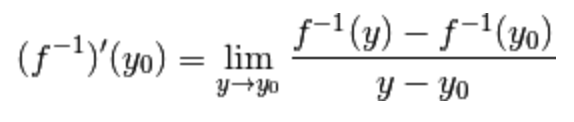
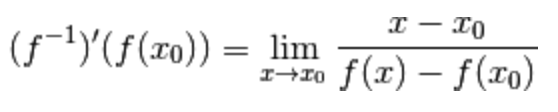
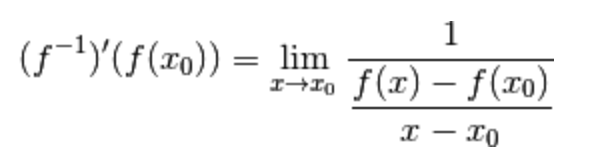
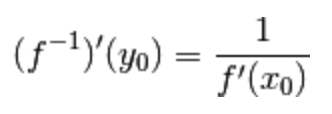
Devi effettuare l'accesso per postare un commento.