RSS

punto singolare di una curva

21 Feb

°°°°°

“La matematica non conosce razze o confini geografici; per la matematica, il mondo culturale è una singola nazione.”

DAVID HILBERT

°°°°°

punto singolare di una curva

In geometria,

un punto singolare di una curva è un punto per il quale la curva non è rappresentata da una funzione liscia.

La definizione precisa dipende dal tipo di curva che si considera.

Curve algebriche nel piano

Una curva algebrica nel piano è definita come il luogo geometrico dei punti $(x,y)$ del piano che soddisfano una equazione nella forma $f(x,y)=0$ dove

$f$ è una funzione polinomiale $f\colon \mathbb{R} ^{2}\to \mathbb{R}$

f(x,y)=a_{0}+b_{0}x+b_{1}y+c_{0}x^{2}+2c_{1}xy+c_{2}y^{2}+\dots

Se l’origine $(0,0)$ appartiene alla curva allora $a_{0}=0$ . Se $b_{1}\neq 0$ allora il teorema delle funzioni implicite assicura che esiste una funzione liscia $h$ tale che la curva ha la forma $y=h(x)$ in un intorno dell’origine.

Analogamente, se $b_{0}\neq 0$ allora esiste una funzione liscia $k$ tale che la curva ha la forma $x=k(y)$ in un intorno dell’origine.

In entrambi i casi, esiste una mappa regolare da $\R$ al piano sul quale è definita la curva in un intorno dell’origine.

Nell’origine si ha che

b_{0}={\partial f \over \partial x},\,b_{1}={\partial f \over \partial y},

per cui la curva è non singolare, o regolare, nell’origine se almeno una delle derivate parziali di $f$ è non nulla.

I punti singolari sono quei punti della curva nei quali si annulla il gradiente di $f$ :

f(x,y)={\partial f \over \partial x}={\partial f \over \partial y}=0.

Punti di regolarità

Assumendo che la curva passi per l’origine e ponendo $y = mx$ , $f$ può essere scritta come

$f=(b_{0}+mb_{1})x+(c_{0}+2mc_{1}+c_{2}m^{2})x^{2}+\dots .\,$

Se $b_{0}+mb_{1}\neq 0$ allora $f=0$ ha una soluzione di molteplicità $1$ per $x=0$ e l’origine è un punto di contatto di ordine $1$ con la retta $y = mx$ .

Se $b_{0}+mb_{1}=0$ allora $f=0$ ha una soluzione di molteplicità maggiore o uguale a $2$ e la retta $y = mx$ ovvero $b_{0}x+b_{1}y=0$ è tangente alla curva. In tale caso, se $c_{0}+2mc_{1}+c_{2}m^{2}\neq 0$ allora la curva ha un punto di contatto di ordine $2$ con $y = mx$ .

Se il coefficiente di ${\displaystyle x^{2))$ è nullo ovvero se $c_{0}+2mc_{1}+c_{2}m^{2}=0$ ma non è nullo il coefficiente di $x^3$ allora l’origine è un punto di flesso della curva.

Se entrambi i coefficienti di ${\displaystyle x^{2))$ e $x^3$ sono nulli allora l’origine è un punto di ondulazione.

Tale analisi si generalizza ad ogni punto della curva, traslandola in modo che il punto di interesse vada a cadere nell’origine.

Punti doppi

Tre limaçon:

la curva a sinistra ha un punto doppio isolato nell’origine,

quella al centro (cardioide) ha una cuspide nell’origine,

quella a destra ha un nodo (autointersezione) nell’origine.

Se ${\displaystyle b_{0))$ e ${\displaystyle b_{1))$ sono entrambi nulli ma almeno uno tra ${\displaystyle c_{0))$ , ${\displaystyle c_{1))$ e ${\displaystyle c_{2))$ è non nullo allora l’origine è un punto doppio per la curva.

Ponendo $y = mx$ , $f$ può essere scritta come

$f=(c_{0}+2mc_{1}+c_{2}m^{2})x^{2}+(d_{0}+3md_{1}+3m^{2}d_{2}+d_{3}m^{3})x^{3}+\dots .\,$

I punti doppi possono essere classificati secondo le soluzioni di $c_{0}+2mc_{1}+c_{2}m^{2}=0$ .

Nodi

Se $c_{0}+2mc_{1}+c_{2}m^{2}=0$ ha due soluzioni reali rispetto a $m$ , ovvero se $c_{0}c_{2}-(c_{1})^{2}<0$ allora l’origine è un nodo per la curva.

In tale caso la curva ha un’autointersezione nell’origine e ha due tangenti distinte corrispondenti alle due soluzioni di $c_{0}+2mc_{1}+c_{2}m^{2}=0$ .

La funzione $f$ ha un punto di sella in corrispondenza.

Punti doppi isolati

Se $c_{0}+2mc_{1}+c_{2}m^{2}=0$ non ha soluzioni reali rispetto a $m$ , ovvero se $c_{0}c_{2}-(c_{1})^{2}>0$ , allora l’origine è un punto doppio isolato (o nodo isolato).

Nel piano reale è quindi un punto isolato, ma se si considera la curva complessa l’origine non è un punto isolato e ha due tangenti immaginarie, corrispondenti alle due soluzioni complesse di $c_{0}+2mc_{1}+c_{2}m^{2}=0$ .

La funzione $f$ ha un estremo locale in corrispondenza.

Cuspidi

Se $c_{0}+2mc_{1}+c_{2}m^{2}=0$

ha una soluzione di molteplicità $2$ rispetto a $m$ , ovvero

$c_{0}c_{2}-(c_{1})^{2}=0$

allora l’origine è un punto di cuspide.

La curva cambia direzione con un angolo netto nell’origine e ha una sola tangente, che può essere considerata come due tangenti coincidenti.

Ulteriori classificazioni

Il numero di nodi o cuspidi di una curva è uno dei due invarianti della formula di Plücker.

Se una delle soluzioni di

$c_{0}+2mc_{1}+c_{2}m^{2}=0$

è anche soluzione di

$d_{0}+3md_{1}+3m^{2}d_{2}+d_{3}m^{3}=0$

allora il ramo corrispondente della curva ha un punto di flesso nell’origine, che in questo caso è un punto di flencnodo.

Se entrambe le tangenti hanno questa proprietà, ovvero

$c_{0}+2mc_{1}+c_{2}m^{2}=0$ è un fattore di

$d_{0}+3md_{1}+3m^{2}d_{2}+d_{3}m^{3}=0$

allora l’origine è un biflecnodo.

Punti multipli

$La curva f ( t ) = ( sin ⁡ ( 2 t ) + cos ⁡ ( t ) , sin ⁡ ( t ) + cos ⁡ ( 2 t ) {\displaystyle f(t)=(\sin(2t)+\cos(t),\sin(t)+\cos(2t)} ha un punto triplo nell'origine$

La curva $f(t)=(\sin(2t)+\cos(t),\sin(t)+\cos(2t)$ ha un punto triplo nell’origine

In generale, se tutti i termini di grado inferiore a $k$ sono nulli, almeno un termine di grado $k$ è non nullo in $f$ e la curva ha un punto multiplo di ordine $k$ .

La curva avrà, in generale, $k$ tangenti nell’origine, anche se alcune di esse possono essere immaginarie.

Curve parametriche

Una curva parametrica in $\R^2$ è definita come l’immagine di una funzione

$g\colon \mathbb{R} \to \mathbb{R} ^{2},\ g(t)=(g_{1}(t),g_{2}(t))$

I punti singolari sono quelli per i quali si annulla il gradiente di $g$ , ovvero

${dg_{1} \over dt}={dg_{2} \over dt}=0.$

Molte curve possono essere definite in questa maniera, ma le definizioni di singolarità possono non essere sempre concordi.

La cuspide è singolare in entrambe le definizioni, un esempio è la curva seguente che ha una cuspide nell’origine, e può essere definita implicitamente come

$x^{3}-y^{2}=0$

o in forma parametrica come

$g(t)=(t^{2},t^{3})$

Nel caso dei nodi non è sempre questo il caso, ad esempio nella curva

$y^{2}-x^{3}-x^{2}=0$

l’origine è un punto singolare se si considera la curva definita implicitamente in forma algebrica, ma considerando la parametrizzazione

$g(t)=(t^{2}-1,t^{3}-t)$

si ha che

$g'(t)=(2t,3t^{2}-1)$

non si annulla mai, e il nodo non è un punto singolare per la parametrizzazione.

È necessario prestare attenzione nella scelta della parametrizzazione:

ad esempio la retta $y=0$ parametrizzata da

$g(t)=(t^{3},0)$

ha una singolarità nell’origine, mentre quando è parametrizzata da $g(t)=(t,0)$ non ha singolarità.

Per questo motivo, è più opportuno parlare di punto singolare di una parametrizzazione regolare piuttosto che di punto singolare della curva in sé.

La precedente definizione può essere estesa per coprire i punti singolari delle curve implicite, che sono definiti come insieme degli zeri $f^((-1))(0)$ di una funzione liscia, e può essere estesa per curve in più dimensioni.

Un teorema di Hassler Whitney afferma che ogni insieme chiuso in $\mathbb {R} ^{n}$ è l’insieme degli zeri

$f^((-1))(0)$

di una opportuna funzione liscia

$f\colon \mathbb{R} ^{n}\to \mathbb{R}$ .

°°°°°

Segue …

Funzione liscia

In matematica, una funzione liscia in un punto del suo dominio è una funzione che è differenziabile infinite volte nel punto, o equivalentemente, che è derivabile infinite volte nel punto rispetto ad ogni sua variabile (per il teorema del differenziale infatti, una funzione è differenziabile in un punto se le sue derivate parziali sono ivi continue).Se una funzione $f$ è liscia in tutti i punti di un insieme $A$ , si dice che essa è di classe $C^{\infty}$ su $A$ , e si scrive $f\in C^{\infty }(A)$

Funzioni lisce e funzioni analitiche nel caso reale

Sia $f:D\to \mathbb{R}$ una funzione reale di variabile reale definita su un dominio $D\subseteq \mathbb{R}$ , e si supponga che $f$ sia liscia sull’intervallo aperto $I\subseteq D$ . Preso allora un punto $x_{0}\in I$ , è possibile approssimare la funzione attorno a quel punto grazie al teorema di Taylor:

f(x)=f(x_{0})+f^{\prime }(x_{0})(x-x_{0})+\ldots +{\frac {f^(((n)))(x_{0})}{n!))(x-x_{0})^{n}+o((x-x_{0})^{n})

dove la quantità $o((x-x_{0})^{n})$ è un resto tale che:

\lim _((x\to x_{0))}{\frac {o((x-x_{0})^{n})}{(x-x_{0})^{n))}=0

Poiché la funzione è liscia, questa approssimazione vale per ogni $n$ . In particolare, è possibile valutare la serie di Taylor della funzione prendendo il limite per $n\to +\infty$ :

T_{f}(x):=f(x_{0})+\sum _((k=1))^((+\infty ))((\frac {f^(((k)))(x_{0})}{k!))(x-x_{0})^{k))

A differenza di quanto ci si potrebbe aspettare, questa serie in generale non converge a $f(x)$ : se la convergenza (puntuale) è verificata, si dice che $f$ è analitica in $x_0$ , e se $A$ è l’insieme dei punti in cui $f$ è analitica si scrive $f\in C^((\omega ))(A)$ . Poiché ogni funzione analitica è in particolare liscia, vale la relazione insiemistica:

C^((\omega ))(A)\subset C^((\infty ))(A)

Un discorso analogo può essere fatto per le funzioni a più variabili reali.

Esempi

La funzione esponenziale è una funzione liscia su tutto l’asse reale, avendo derivate di qualsiasi ordine, ciascuna multipla di se stessa:

f(x)=e^((\alpha x))\Rightarrow f^(((n)))(x)=\alpha ^{n}e^((\alpha x))\ \ \forall x\in \mathbb{R}

Si dimostra che tale funzione è anche analitica su tutto l’asse reale, ossia la sua serie di Taylor converge a

e^((\alpha x))

per ogni

x

reale.

La seguente funzione definita a tratti:

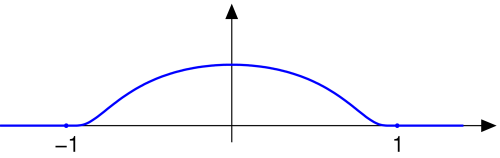
Una funzione liscia non è necessariamente analitica.

f(x)={\begin{cases}e^(({\frac {1}{x^{2}-1))))&{\mbox{ se ))|x|<1,\\0&{\mbox{ altrove ))\end{cases))

è un esempio di funzione liscia ma non analitica sull’intero asse reale. Infatti, si consideri ad esempio il punto

x=1

: tutte le derivate destre della funzione in quel punto sono banalmente nulle, mentre le derivate sinistre valgono:

f^(((n))){(1)}=\lim _((x\to 1^{-))}{e^(({\frac {1}{x^{2}-1)))){\frac {d^{n)){dx^{n))}{(1-x^{2})^((-1))))=0

poiché l’esponenziale decresce più rapidamente di qualunque funzione algebrica. Dal momento che tutte le derivate sinistre e destre combaciano, la funzione è infinitamente derivabile (si dice anche che “si incolla bene”) in

x=1

. Tuttavia, si vede anche che la serie di Taylor della funzione scritta attorno a tale punto risulta identicamente nulla, mentre

f

è non nulla in qualunque intorno sinistro di

x=1

; la funzione non è perciò analitica in tale punto.

Funzioni lisce complesse

Nel caso di funzioni complesse di variabile complessa, la liscezza in un punto (o su un insieme) discende direttamente dall’olomorfia della funzione in tale punto (o su tale insieme). Per tale motivo si parla indifferentemente di “liscezza” o di “derivabilità” di una funzione complessa. In effetti, è possibile dimostrare che una funzione complessa olomorfa su un dominio è ivi addirittura analitica (vedi Equazioni di Cauchy-Riemann).

Definizione per le varietà differenziabili

Siano $M$ e $N$ varietà differenziabili e $p$ un punto di $M$ . Una funzione $F:M\rightarrow N$ è detta differenziabile in $p$ (oppure liscia o di classe $C^\infty$ in $p$ ) se esistono una carta $(U,\phi )$ in $p$ ed una carta $(V,\psi )$ in $F(p)$ tali che $F(U)\subset V$ e la composizione:

\psi \circ \ F\circ \phi ^((-1)):\phi (U)\rightarrow \psi (V)

sia liscia in un intorno di $\phi (p)$ . Tale definizione non dipende dalle carte scelte: prendendo infatti altre carte $(U',\phi ')$ e $(V',\phi ')$ la composizione $\psi '\circ \ F\circ \phi '^((-1))$ rimane liscia in un intorno di $\phi (p)$ .

$F$ è differenziabile (liscia, di classe $C^\infty$ ) se lo è per ogni $p$ in $M$ . Se inoltre $F$ è invertibile con inversa liscia allora $F$ si dirà un diffeomorfismo. Lo studio delle proprietà invarianti per diffeomorfismi è oggetto della topologia differenziale.

Costruire funzioni lisce tramite restrizioni

È spesso utile costruire funzioni lisce che sono nulle al di fuori di un dato intervallo, ma non all’interno dello stesso (funzioni a supporto compatto).

Tale proprietà non si può mai avere per una serie di potenze, il che fornisce un’ulteriore dimostrazione del divario tra le funzioni lisce e funzioni analitiche.

Funzione analitica

In matematica, una funzione analitica è una funzione localmente espressa da una serie di potenze convergente.

Spesso il termine “funzione analitica” è utilizzato come sinonimo di funzione olomorfa, sebbene quest’ultimo si utilizzi più spesso per le funzioni complesse (tutte le funzioni olomorfe sono funzioni analitiche complesse e viceversa).

Una funzione è analitica se e solo se, preso comunque un punto appartenente al dominio della funzione, esiste un suo intorno in cui la funzione coincide col suo sviluppo in serie di Taylor.

Le funzioni analitiche possono essere viste come un ponte fra i polinomi e le funzioni generiche.

Esistono le funzioni analitiche reali e le funzioni analitiche complesse: simili in alcuni aspetti, differenti in altri.

Funzioni di questo tipo sono infinitamente derivabili, ma le funzioni analitiche complesse esibiscono proprietà che generalmente non appartengono alle funzioni analitiche reali.

Definizione

Una funzione $f$ è analitica su un insieme aperto $D$ della retta reale se per ogni $x_0$ in $D$ si può scrivere $f(x)$ come:

f(x)=\sum _((n=0))^{\infty }a_{n}\left(x-x_{0}\right)^{n}=a_{0}+a_{1}(x-x_{0})+a_{2}(x-x_{0})^{2}+a_{3}(x-x_{0})^{3}+\cdots

dove i coefficienti $a_{0},a_{1},\cdots$ sono numeri reali e la serie è convergente in un intorno di $x_0$ .

In alternativa, una funzione analitica è una funzione infinitamente derivabile, ossia una funzione liscia, tale che la sua serie di Taylor

T(x) = \sum_{n=0}^{\infin} \frac{f^{(n)}(x_0)}{n!} (x-x_0)^{n}

in ogni punto $x_0$ appartenente al dominio, converge a $f(x)$ per $x$ in un intorno di $x_0$ .

L’insieme di tutte le funzioni analitiche reali appartenenti ad un dato insieme $D$ si denota di solito come $C^\omega(D)$ .

Una funzione $f$ definita in un qualche sottoinsieme della retta reale, si dice essere reale analitica al punto $x$ se esiste un intorno $D$ di $x$ nel quale $f$ è reale analitica.

La definizione di funzione analitica complessa è ottenuta sostituendo dappertutto “reale” con “complesso”.

Proprietà delle funzioni analitiche

Tra le principali proprietà che caratterizzano le funzioni analitiche ci sono le seguenti:

La somma, il prodotto e la composizione di funzioni analitiche sono analitiche.
Il reciproco di una funzione analitica che non si annulla mai, è analitico, così come l’inversa di una funzione analitica invertibile la cui derivata non è mai nulla.
Tutti i polinomi sono funzioni analitiche. Per un polinomio, l’espansione in serie di potenze contiene solo un numero finito di termini non nulli.
Tutte le funzioni analitiche sono lisce.

Un polinomio non può valere zero in troppi punti a meno che non sia il polinomio nullo (più precisamente, il numero di zeri è al massimo pari al grado del polinomio). Un’affermazione simile ma più debole vale per le funzioni analitiche. Se l’insieme degli zeri di una funzione analitica $f$ ha un punto di accumulazione all’interno del suo dominio, allora $f$ è nulla su tutta la componente connessa del dominio che contiene il punto di accumulazione.

Più formalmente questa affermazione può essere espressa nel modo seguente. Se $(r_n)$ è una successione di numeri distinti tale che $f(r_n)=0$ per ogni $n$ e questa successione converge a un punto $r$ nel dominio $D$ , allora $f$ è identicamente zero nella componente connessa di $D$ contenente $r$ . Inoltre, se tutte le derivate di una funzione analitica sono nulle in un punto, vale ancora la conclusione precedente.

Queste affermazioni implicano che le funzioni analitiche siano ancora abbastanza rigide, nonostante il loro maggior numero di gradi di libertà rispetto ai polinomi.

Analiticità e derivabilità

Tutte le funzioni analitiche (reali o complesse) in un punto $x_0$ sono infinitamente derivabili in $|x-x_0|<R$ , dove $R$ è il raggio di convergenza della serie. Inoltre, si dimostra che nella stessa regione la derivata della funzione coincide con la serie delle derivate (la serie derivata), ovvero se:

f(x)=\sum _{k=0}^{\infty }{a_{k}(x-x_{0})^{k))

allora:

f^{\prime }(x)=\sum _{k=0}^{\infty }{ka_{k}(x-x_{0})^{k-1))

Allo stesso modo, essendo il limite uniforme di una successione di funzioni continue (polinomi), ogni funzione analitica è continua (e quindi integrabile) su tutto il suo insieme di convergenza, e la sua primitiva è la serie primitiva. In altre parole, se:

f(x)=\sum _{k=0}^{\infty }{a_{k}x^{k))

si ha:

\int f(x)dx=\sum _{k=0}^{\infty }((\frac {a_{k)){k+1))x^{k+1))

Non tutte le funzioni reali lisce sono analitiche; ad esempio la funzione definita come:

f(x)=\begin{cases}\exp(-1/x)&\text{se }x>0 \\ 0&\text{se }x\le0 \end{cases}

è liscia in $x=0$ ma non è analitica in 0.

Questo può essere espresso dall’implicazione (non invertibile):

f\in C^{\omega }(E)\Rightarrow f\in C^{\infty }(E)\quad {\text{se ))f:E\subseteq \mathbb {R} \to \mathbb {R}

La situazione è molto diversa nel caso delle funzioni analitiche complesse. Si può dimostrare che tutte le funzioni olomorfe su un insieme aperto sono analitiche.

Di conseguenza, in analisi complessa,

il termine “funzione analitica” è un sinonimo di funzione olomorfa.

Condizione sufficiente

Se una funzione reale di variabile reale liscia definita su un aperto ha tutte le derivate maggiorabili dai termini di una successione geometrica (di ragione fissata) su un intorno di un dato punto, allora la funzione è analitica in quell’intorno.

Formalmente, sia $f : (a,b) \to \mathbb{R}$ ed appartenente a $C^{\infty}(a,b)$ e sia $x_0 \in (a,b)$ .

Se esistono $\Lambda, M, \delta > 0$ tali che:

\left| f^{(k)}(x) \right| \le \Lambda M^{k} \qquad \forall k \ge 0 \quad \forall x \in (x_0 - \delta, x_0 + \delta)

allora:

f(x) = \sum_{k = 0}^{\infty} \frac{ f^{(k)}(x_0)}{k!}(x - x_0)^{k} \qquad \forall x \in (x_0 - \delta, x_0 + \delta)

In particolare, se una funzione ha tutte le derivate limitate da una stessa costante $\Lambda$ su un intervallo, allora è ivi analitica (basta porre $M = 1$ nell’enunciato precedente).

Questo mostra che funzioni come seno, coseno, esponenziale, funzioni iperboliche possono essere espresse in termini di serie di potenze sull’intero asse reale:

e^x = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \cdots

\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots

\cos x = 1 - \frac{x^2}{2} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots

\sinh x = x + \frac{x^3}{3!} + \frac{x^5}{5!} + \frac{x^7}{7!} + \cdots

\cosh x = 1 + \frac{x^2}{2} + \frac{x^4}{4!} + \frac{x^6}{6!} + \cdots

Dimostrazione

Dato che la funzione $f$ è liscia, è possibile scriverne la formula di Taylor arrestata all’ordine $n - 1$ (resto secondo Lagrange):

f(x) = \sum_{k=0}^{n-1}\frac{f^{(k)}(x_0)}{k!}(x - x_0)^{k} + \frac{f^{(n)}(\xi)}{n!}(x - x_0)^{n} \quad \xi \in (x_0 - x, x_0 + x)

Se $x$ si muove nell’intorno di $x_0$ di raggio $\delta$ si può usare la maggiorazione (in valore assoluto) garantita dall’ipotesi:

\left| f(x) - \sum_{k=0}^{n-1}\frac{f^{(k)}(x_0)}{k!}(x - x_0)^{k} \right| = \left| \frac{f^{(n)}(\xi)}{n!}(x - x_0)^{n} \right| \le \frac{\Lambda M^{n)){n!}\delta^{n} = \Lambda \frac{(M\delta)^{n)){n!} \underset{n \longrightarrow +\infty}{\longrightarrow} 0

cioè la serie converge puntualmente a $f$ sull’intervallo $(x_0 - \delta, x_0 + \delta)$ ,

Q.E.D.

Funzioni analitiche reali e complesse

Le funzioni analitiche reali e complesse hanno importanti differenze, come si può vedere dalla loro differente relazione con la derivabilità.

Le funzioni analitiche complesse sono più rigide in molti sensi.

Secondo il teorema di Liouville, ogni funzione analitica complessa limitata definita sull’intero piano complesso è costante. Questa affermazione è chiaramente falsa per una funzione analitica reale, come si vede da

f(x)=\frac{1}{x^2+1}

Inoltre, se una funzione analitica complessa è definita in una palla aperta intorno a un punto $x_0$ , la sua espansione in serie di potenze in $x_0$ è convergente nell’intera palla. Questo non è vero in generale per le funzioni analitiche reali. Una palla aperta nel piano complesso è un disco bidimensionale, mentre sulla retta reale è un intervallo.

Ogni funzione analitica reale su un certo insieme aperto della retta reale può essere estesa a una funzione analitica complessa su un certo insieme aperto del piano complesso.

Comunque non tutte le funzioni analitiche reali definite sull’intera retta reale possono essere estese a una funzione complessa definita sull’intero piano complesso.

La funzione $f(x)$ definita nel paragrafo precedente è un controesempio.

Funzioni analitiche in più variabili

Si possono definire le funzioni analitiche in più variabili tramite le serie di potenze in queste variabili.

Le funzioni analitiche in più variabili hanno alcune delle proprietà delle funzioni analitiche a una variabile. Comunque, soprattutto nel caso delle funzioni analitiche complesse, si trovano nuovi e interessanti fenomeni in più dimensioni.

°°°°°

Teorema delle funzioni implicite

In matematica, in particolare in analisi matematica e geometria, il teorema delle funzioni implicite è un importante strumento che stabilisce quando il luogo di zeri di un’equazione implicita si può esplicitare rispetto a una variabile.

Nella letteratura italiana, il teorema è generalmente detto teorema di Dini in onore del matematico Ulisse Dini, che contribuì ad estenderne la formulazione.

Il teorema di Dini

Il teorema di Dini stabilisce che una funzione reale di classe $C^1$ di due variabili del tipo:

F(x,y)

definisce implicitamente un’unica funzione del tipo:

y=f(x)

in un intorno di un punto $(a,b)$ tale che (esplicitando rispetto alla variabile y):

F(a,b)=0\qquad {\frac {\partial F}{\partial y))(a,b)\neq 0

Il teorema di Dini fornisce quindi una condizione sufficiente affinché esista un’unica funzione $y=f(x)$ tale che

F(x,f(x))=0

sia soddisfatta al variare di $x$ , ovvero un’unica funzione

$x=g(y)$

tale che

F(g(y),y)=0

sia soddisfatta al variare di $y$ .

Questo non significa che sia possibile esplicitare una delle due incognite in funzione dell’altra, ovvero che sia possibile trovare $y=f(x)$ oppure $x=g(y)$ in forma esplicita, ma mostra piuttosto che esiste almeno una delle due funzioni, detta funzione implicita.

Se ci si limita all’individuazione di particolari tipi di funzione, ad esempio quelle continue e definite su un intervallo, si può dimostrare anche la loro unicità, il che sancisce un’equivalenza formale tra la scrittura implicita $F(x,y)=0$ e quella esplicita $y=f(x)$ oppure $x=g(y)$ . Ad esempio, l’equazione:

F(x,y)=y+x^{2}e^{y}=0

ben definisce un’unica funzione continua $y=f(x)$ definita per ogni $x$ reale, che tuttavia non può essere scritta esplicitamente.

Enunciato

Sia $F:G\subset \mathbb{R} ^{2}\to \mathbb{R}$ una funzione a valori reali, differenziabile e le cui derivate parziali prime siano funzioni continue.

Sia inoltre $(x_{0},y_{0})\in G$ tale che:

F(x_{0},y_{0})=0\qquad {\frac {\partial F}{\partial y))(x_{0},y_{0})\neq 0\

Il teorema afferma che esiste una funzione derivabile reale:

g:[x_{0}-h,x_{0}+h]\to [y_{0}-k,y_{0}+k]\qquad h,k>0\quad h,k\in \mathbb{R}

la cui derivata prima sia continua. Inoltre, il grafico di $g$ è l’insieme delle coppie:

\{(x,y)\in G:F(x,y)=0\}

che sono contenute nel rettangolo:

[x_{0}-h,x_{0}+h]\times [y_{0}-k,y_{0}+k]

Il teorema in due dimensioni

Si consideri una funzione di classe C¹ $F:A\to \mathbb{R}$ definita su un insieme aperto $A\subseteq \mathbb{R} ^{2}$ , e si consideri l’insieme:

Z=\{(x,y)\in A:F(x,y)=0\}

Se $Z$ è non vuoto esiste un punto $(x_0,y_0)$ tale che:

F(x_{0},y_{0})=0\

Il teorema afferma che se $(x_0,y_0)$ non è un punto critico, ovvero:

\nabla F(x_{0},y_{0})\neq 0\

allora esiste un intorno $U$ di $(x_0,y_0)$ tale che l’insieme $Z\cap U$ è il grafico di una funzione derivabile.

Questo equivale a dire che esiste un’unica funzione del tipo $y=y(x)$ o del tipo $x=x(y)$ che mette in relazione le due incognite $x$ e $y$ . Si noti che questo non significa che è davvero possibile esplicitare una delle due variabili in funzione dell’altra, ma solo che l’equazione definisce implicitamente un legame tra le due incognite che è univoco.

Sia $g:A\subset \mathbb{R} ^{2}\rightarrow \;{\mathbb {R))$ una funzione di classe ${\mathcal {C))^{1}$ nell’aperto $A$

sia $(x_{0},y_{0})\in A$ tale che:

g(x_{0},y_{0})=0\qquad g_{y}(x_{0},y_{0})\neq 0

Allora esistono un intervallo reale aperto $I$ , con $x_{0}\in I$ , un intervallo reale aperto $J$ , con $y_{0}\in J$ , ed una funzione $y(x)$ di classe ${\mathcal {C))^{1}$ in $I$ a valori in $J$ tali che:

y(x_{0})=y_{0}\qquad y'(x_{0})=-\left({\frac {g_{x}(x_{0},y_{0})}{g_{y}(x_{0},y_{0})))\right)

e tali che per ogni $x\in I,y\in J$ la relazione:

g(x,y)=0\

si verifica se e solo se:

y=y(x)\

Scambiando i ruoli delle variabili si giunge a definire una funzione

$x=x(y)$ .

Dimostrazioni

Prima dimostrazione

Sia data una funzione continua $g:A\subset \mathbb{R} ^{2}\to \mathbb{R}$ di classe ${\mathcal {C))^{1}$ in $A$ tale che $\nabla g(x,y)\neq 0$ in tutti i punti tali che $g(x,y)=0$ , cioè nella curva di livello:

V=\{(x,y)\in A:g(x,y)=0\}

Sia $(x_0,y_0)$ un punto di $V$ e si consideri il relativo sviluppo al primo ordine di Taylor:

g(x,y)=g(x_{0},y_{0})+g_{x}(x_{0},y_{0})(x-x_{0})+g_{y}(x_{0},y_{0})(y-y_{0})+o({\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2))})

Tenendo conto che $g(x_{0},y_{0})=0$ , uguagliando a zero la prima parte del termine al primo ordine si ottiene:

g_{x}(x_{0},y_{0})(x-x_{0})+g_{y}(x_{0},y_{0})(y-y_{0})=0\,

Per ipotesi, tale equazione di primo grado ha almeno un coefficiente diverso da zero, e si può porre $g_{y}(x_{0},y_{0})\neq 0$ . Si può quindi ricavare $y$ in funzione di $x$ :

y=y_{0}-{\frac {g_{x}(x_{0},y_{0})}{g_{y}(x_{0},y_{0})))(x-x_{0})

Il teorema mostra che l’errore nella formula di approssimazione al primo ordine non incide sulla possibilità di esprimere una variabile in funzione dell’altra.

La funzione ottenuta ha sviluppo al primo ordine:

y=y_{0}-{\frac {g_{x}(x_{0},y_{0})}{g_{y}(x_{0},y_{0})))(x-x_{0})+o(x-x_{0})

Seconda dimostrazione (Teorema delle contrazioni)

Sia data una funzione continua $g:A\subseteq \mathbb {R} ^{2}\rightarrow \mathbb {R}$ di classe ${\mathcal {C))^{1}$ nell’aperto $A$ tale che per $(x_{0},y_{0})\in A$ si abbia

{\begin{aligned}g(x_{0},y_{0})=0\;\;\;\;\;g_{y}(x_{0},y_{0})\neq 0\end{aligned)).

Sia definita la funzione

{\begin{aligned}G(x,y)=y-{\frac {g(x,y)}{g_{y}(x_{0},y_{0})))\end{aligned)).

allora ${\displaystyle G(x_{0},y_{0})=y_{0))$ e $G(x,y)=y$ per $(x,y)\in I\times J$ . Dunque trovare gli zeri di $g(x,y)$ si riduce a trovare il punto fisso della funzione $G(x,y)$ .

Grazie al teorema delle contrazioni sappiamo che, definito

{\displaystyle X=\{\psi :I\rightarrow J\;|\;\psi \in {\mathcal {C))^{0}\))

siccome $G\in X$ , $(X,\lVert \cdot \lVert _{\infty })$ è facile dimostrare che sia uno spazio metrico completo, allora

\exists !\;y=f(x):G(x,f(x))=f(x)

Sia $H:X\rightarrow X$ una contrazione tale che

w\mapsto H[w](x)=G(x,w(x))

ci basta dimostrare che $H$ sia ben definita, cioè che $H[w]\in X$ . Questa deve avere le seguenti proprietà:

$H[w]$ è continua in $I$
$\lVert H[w]-y_{0}\rVert _{\infty }\leq \varepsilon$

La prima è ovvia siccome l’operatore è composizione di funzioni continue.

La seconda può essere dimostrata tramite una catena di disuguaglianze

{\begin{aligned}&\lVert H[w]-y_{0}\rVert _{\infty }=\lVert G(x,w(x))-G(x_{0},y_{0})\lVert _{\infty }\leq \lVert G(x,w(x))-G(x,y_{0})\lVert _{\infty }+\lVert G(x,y_{0})-G(x_{0},y_{0})\lVert _{\infty }=\\[10pt]&=\lVert G(x,w(x))-G(x,y_{0})\lVert _{\infty }+\lVert y_{0}-{\frac {g(x,y_{0})}{g_{y}(x_{0},y_{0})))-y_{0}\lVert _{\infty }\leq \lVert G_{y}(x,\xi _{y})(w(x)-y_{0})\lVert _{\infty }+{\frac {\lVert g(x,y_{0})\lVert _{\infty )){|g_{y}(x_{0},y_{0})|))\leq \\[10pt]&\leq {\underset {\xi _{y}\in J}{\sup ))|G_{y}(x,\xi _{y})|\lVert w(x)-y_{0}\lVert _{\infty }+{\frac {\lVert g(x,y_{0})\lVert _{\infty )){|g_{y}(x_{0},y_{0})|))\leq \varepsilon \end{aligned))

dove si è applicato il teorema di Lagrange ed il fatto che

{\begin{aligned}&{\underset {\xi _{y}\in J}{\sup ))G_{y}(x,\xi _{y})\leq {1 \over 2}\;\;{\text{ siccome ))h,k\;{\text{ possono essere piccoli a piacimento))\\[10pt]&\lVert w(x)-y_{0}\lVert _{\infty }\leq \varepsilon \;\;{\text{ siccome ))w(x)\in X\\[10pt]&{\frac {\lVert g(x,y_{0})\lVert _{\infty )){|g_{y}(x_{0},y_{0})|))\leq {\varepsilon \over 2}\end{aligned))

Ora basta dimostrare che $H$ sia una contrazione:

{\displaystyle \lVert H[w]-H[v]\lVert _{\infty }=\lVert G(x,w(x))-G(x,h(x))\lVert _{\infty }\leq {\underset {\xi \in J}{\sup ))|G(x,\xi )|\lVert w-v\lVert _{\infty }\leq {1 \over 2}\lVert w-v\lVert _{\infty ))

Il teorema in più dimensioni

Sia ${\mathbf f}:E\subset \mathbb{R} ^((n+m))\rightarrow \mathbb{R} ^{n}$ una funzione di classe ${\mathcal {C))^{1}$ , dove $\mathbb{R} ^((n+m))$ è il prodotto cartesiano $\mathbb{R} ^{n}\times \mathbb{R} ^{m}$ i cui elementi sono del tipo $({\mathbf {x)),{\mathbf {y)))=(x_{1},x_{2},\ldots ,x_{n},y_{1},y_{2},\ldots ,y_{m})$ .

Sia inoltre $({\mathbf {a)),{\mathbf {b)))=(a_{1},a_{2},\ldots ,a_{n},b_{1},b_{2},\ldots ,b_{m})\in E$ un punto tale che ${\mathbf f}({\mathbf {a)),{\mathbf {b)))=0$ .

Data la matrice jacobiana di $\mathbf f$ in $({\mathbf {a)),{\mathbf {b)))$ :

{\begin{matrix}(D{\mathbf f})({\mathbf {a)),{\mathbf {b)))&=&\left[{\begin{matrix}{\frac {\partial f_{1)){\partial x_{1))}({\mathbf {a)),{\mathbf {b)))&\cdots &{\frac {\partial f_{1)){\partial x_{n))}({\mathbf {a)),{\mathbf {b)))\\\vdots &\ddots &\vdots \\{\frac {\partial f_{n)){\partial x_{1))}({\mathbf {a)),{\mathbf {b)))&\cdots &{\frac {\partial f_{n)){\partial x_{n))}({\mathbf {a)),{\mathbf {b)))\end{matrix))\right|\left.{\begin{matrix}{\frac {\partial f_{1)){\partial y_{1))}({\mathbf {a)),{\mathbf {b)))&\cdots &{\frac {\partial f_{1)){\partial y_{m))}({\mathbf {a)),{\mathbf {b)))\\\vdots &\ddots &\vdots \\{\frac {\partial f_{n)){\partial y_{1))}({\mathbf {a)),{\mathbf {b)))&\cdots &{\frac {\partial f_{n)){\partial y_{m))}({\mathbf {a)),{\mathbf {b)))\\\end{matrix))\right]={\begin{bmatrix}X&|&Y\end{bmatrix))\\\end{matrix))

si supponga che $X$ è invertibile.

Il teorema delle funzioni implicite afferma che vi sono due insiemi aperti $U\subset \mathbb{R} ^((n+m))$ e $V\subset \mathbb{R} ^{m}$ contenenti rispettivamente $({\mathbf {a)),{\mathbf {b)))$ e $\mathbf{b}$ tali che per ogni ${\mathbf {y))\in V$ esiste un unico $\mathbf{x}$ che soddisfa $({\mathbf {x)),{\mathbf {y)))\in U$ e ${\mathbf f}({\mathbf {x)),{\mathbf {y)))=0$ .

Inoltre, la funzione ${\mathbf g}:V\to \mathbb{R} ^{n}$ tale che ${\mathbf g}({\mathbf {y)))={\mathbf {x))$ è una funzione di classe ${\mathcal {C))^{1}$ tale che:

{\mathbf g}({\mathbf {b)))={\mathbf {a))\qquad (D{\mathbf g})({\mathbf b})=-X^((-1))Y

dove $(D{\mathbf g})({\mathbf b})$ è la jacobiana di ${\mathbf g}$ in $\mathbf{b}$ . La relazione:

{\mathbf f}({\mathbf g}({\mathbf y}),{\mathbf y})=0\qquad {\mathbf y}\in V

definisce implicitamente ${\mathbf g}$ .

Il teorema stabilisce quindi che il sistema ${\mathbf {f))({\mathbf {x)),{\mathbf {y)))={\mathbf 0}$ :

\left\((\begin{matrix}f_{1}(x_{1},x_{2},\cdots ,x_{n},y_{1},y_{2},\cdots ,y_{m})=0\\f_{2}(x_{1},x_{2},\cdots ,x_{n},y_{1},y_{2},\cdots ,y_{m})=0\\\vdots \\f_{n}(x_{1},x_{2},\cdots ,x_{n},y_{1},y_{2},\cdots ,y_{m})=0\\\end{matrix))\right.

può essere risolto esplicitando $(x_{1},x_{2},\cdots ,x_{n})$ in funzione di $(y_{1},y_{2},\cdots ,y_{m})$ in un intorno di $\mathbf{b}$ se il sistema è risolvibile in $({\mathbf {a)),{\mathbf {b)))$ e se $X$ è invertibile.

Le soluzioni così trovate sono inoltre funzioni di classe ${\mathcal {C))^{1}$ . Il teorema può essere generalizzato al caso di funzioni analitiche.

Il teorema si estende anche agli spazi di Banach.

Lascia un commento

Pubblicato da salvatore di lucia su 21 febbraio 2021 in MATEMATICA

Tag: Curve algebriche nel piano, Punti di regolarità, punto singolare di una curva

Lascia un commento Cancella risposta

WebMaster : Salvatore Di Lucia

iMathematica :
più La si visita più Vi aiuta a risolvere ... iProblemi ...!
Statistiche del Sito:
- 1.043.687 visite
Ricerca Articolo
Cerca
Calendario
febbraio: 2021

L M M G V S D

1 2 3 4 5 6 7

8 9 10 11 12 13 14

15 16 17 18 19 20 21

22 23 24 25 26 27 28

« Gen Mar »
Traduttore
I Grandi Matematici
Questo slideshow richiede JavaScript.
Visitatori del Sito :

Free counters
Grandi Matematici
Questo slideshow richiede JavaScript.
Categorie
Categorie
Articoli Mese
Articoli Mese
Giugno 2024

– Analisi Matematica I

— Grafici di funzioni

—Derivate

Maggio 2024

– Analisi Matematica I

— Grafici di funzioni

—Limiti
Aprile 2024

– Analisi Matematica I

— Numeri Reali

—Funzioni
Marzo 2024

– Analisi Matematica I

— Teoria degli Insiemi

—Relazioni Matematiche
Febbraio 2024

– Logica Matematica

— Tavole Verità

—Tautologie
Gennaio 2024

– Logica Matematica

— Proposizione logica

— Connettivi Logici
Dicembre 2023

– Algebra I

— Funzione di Eulero

— Teorema di Eulero
Novembre 2023

– Algebra I

— Divisibilità Partizioni

— Congruenze in
Ottobre 2023

– Analisi I

— Successioni di numeri reali

— Esercitazioni
Settembre 2023

– Analisi I

— Funzioni

— Segno di Funzione
Agosto 2023

– Algebra

— Equazioni

— Disequazioni
Luglio 2023

– Algebra

— Strutture Algebriche
Giugno 2023

– Calcolo Combinatorio

— Coefficiente Binomiale
Maggio 2023

– Funzioni Polinomiali

— Scomposizione di Polinomi
Aprile 2023

– Funzioni Reale di variabile Reale

— Studio di Funzione
Marzo 2023

– Funzioni Reale di variabile Reale

— Studio di Funzione
Febbraio 2023

– Insieme dei Numeri Complessi

— ℂ
Gennaio 2023

– Insiemi Numerici

— ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ=ℚ ∪ 𝕀
Dicembre 2022

– Algebra Lineare

— Sistemi Lineari

—Esercitazione
Novembre 2022

– Algebra Lineare

— Matrice, Determinante

—Esercitazione
Ottobre 2022

– Analisi I

— Integrali

—Esercitazione
Settembre 2022

– Analisi I

— Derivata

—Esercitazione
Agosto 2022

– Analisi I

— Teoremi sui Limiti

—Esercitazione
Luglio 2022

– Analisi I

— Teoria dei Limiti

—Esercitazione
Giugno 2022

– Analisi II

— Equazioni Differenziali

—Esercitazione
Maggio 2022

– Analisi II

— Equazioni Differenziali

—Esercitazione
Aprile 2022

– Analisi II

— Equazioni Differenziali
Marzo 2022

– Analisi II

— Equazioni Differenziali
Febbraio 2022

– Analisi I

— Integrali
Gennaio 2022

– Analisi I

— Derivate
Dicembre 2021

– Algebra

— Polinomi
Novembre 2021

– Corso di Analisi II

— Topologia Generale
Ottobre 2021

– Corso di Analisi II

— Equazioni Differenziali
Settembre 2021

– Corso di Analisi

— Coniche

— Quadriche
Agosto 2021

– Corso di Analisi

— Classificazione delle Funzioni
Luglio 2021

– Corso di Analisi

— Successioni Numeriche
Giugno 2021

– Corso di Analisi

— Serie Numeriche
Maggio 2021

– Corso di Analisi

— Serie Numeriche
Aprile 2021

– Corso di Analisi

—Tipi di Funzioni
Marzo 2021

– Corso di Analisi

—Tipi di Funzioni
Febbraio 2021

– Corso di Analisi

—Confronto tra Funzioni
Gennaio 2021

– Corso di Analisi

—Confronto tra Funzioni
Dicembre 2020

– Corso di Analisi

—Limiti Teoremi
Novembre 2020

– Corso di Analisi

—Limiti
Ottobre 2020

– Corso di Analisi

—o-piccolo

_O-grande

_Esercizi sui Limiti
Settembre 2020

– Corso di Analisi

—Punto di accumulazione

—Simboli di Landau
Agosto 2020

– Corso di Analisi

—Classe di resto modulo n

__Equazioni Congruenziali
Luglio 2020

– Corso di Analisi

—Classe di resto modulo n

__Equazioni Congruenziali
Giugno 2020

– Corso di Analisi

—Classe di resto modulo n

__Equazioni Congruenziali
Maggio 2020

– Corso di Analisi

—Classe di resto modulo n

__Equazioni Congruenziali
Aprile 2020

– Corso di Analisi

—Classe di resto modulo n

__Equazioni Congruenziali
Marzo 2020

– Corso di Analisi

—Le Coniche
Febbraio 2020

– Corso di Analisi

—Le Coniche
Gennaio 2020

– Corso di Analisi

—Le Coniche
Dicembre 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia e Esercizi
Novembre 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia e Esercizi
Ottobre 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia e Esercizi
Settembre 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia e Esercizi
Agosto 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia e Esercizi
Luglio 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia
Giugno 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia
Maggio 2019

– Corso di Analisi

—Istituzione di Analisi Superiore
Aprile 2019

– Corso di Analisi

—Istituzione di Analisi Superiore
Marzo 2019

– Corso di Analisi

—Istituzione di Analisi Superiore
Febbraio 2019

– Corso di Analisi

—Istituzione di Analisi Superiore
Gennaio 2019

– Corso di Analisi

—Istituzione di Analisi Superiore
Gennaio 2018

– Corso di Analisi

—Teoria degli Insiemi
Dicembre 2018

– Corso di Analisi

—Istituzione di Analisi Superiore
Novembre 2018

– Corso di Analisi

—Istituzione di Analisi Superiore
Ottobre 2018

– Corso di Analisi

—Istituzione di Analisi Superiore
Settembre 2018

– Corso di Analisi

—Istituzione di Analisi Superiore
Agosto 2018

– Corso di Analisi

—Esercizi sui Numeri Complessi
Luglio 2018

– Corso di Analisi

—Esercizi sui Numeri Complessi
Giugno 2018

– Corso di Analisi

—Insieme dei Numeri Complessi
Maggio 2018

– Corso di Analisi

—Teoria dei Numeri
Aprile 2018

– Corso di Analisi

—Teoria degli Insiemi
Marzo 2018

– Corso di Analisi

—Teoria degli Insiemi
Febbraio 2018

– Corso di Analisi

—Teoria degli Insiemi
Dicembre 2017

– Corso di Analisi I
—Manuale di iMathematica
Novembre 2017

– Corso di Analisi I
—Manuale di iMathematica
Ottobre 2017

– Corso di Analisi I
—Manuale di iMathematica
Settembre 2017

– Corso di Analisi I
—Manuale di iMathematica
Agosto 2017

– Corso di Analisi I
—Manuale di iMathematica
Luglio 2017

– Corso di Analisi I
—Manuale di iMathematica
Giugno 2017

– Corso di Analisi I
—Manuale di iMathematica
Maggio 2017

- Corso di Analisi
--Trasformazioni Lineari
Aprile 2017

- Corso di Analisi
--Equazioni Differenziali Lineari
Marzo 2017

- Corso di Analisi
--Equazioni Differenziali Ordinarie
Febbraio 2017

- Corso di Analisi
--Precorso
Gennaio2017

- Corso di Analisi
--Serie Trigonometriche
Dicembre 2016

- Corso di Analisi
--Strutture Fondamentali dell'Analisi
Novembre 2016

- Corso di Analisi
--Strutture Fondamentali dell'Analisi
Ottobre 2016

- Corso di Analisi
--Strutture Fondamentali dell'Analisi
Settembre 2016

- Corso di Analisi
-- Integrali Impropri
Agosto 2016

- Corso di Analisi
-- Funzioni Analitiche
Luglio 2016

- Corso di Analisi
-- Integrale Curvilineo
Giugno 2016

- Corso di Analisi
-- Integrale definito
Maggio 2016

- Corso di Analisi
-- Integrale di Riemann
Aprile 2016

- Corso di Analisi
-- Derivate di ordine superiore
Marzo 2016

- Corso di Analisi
-- Derivate
Febbraio 2016

- Corso di Analisi
-- Esercizi sulle Serie
Gennaio 2016

- Corso di Analisi
-- Serie
Dicembre 2015

– Corso di Analisi
— Successioni di funzioni
Novembre 2015

- Corso di Analisi
-- Funzioni Continue
Ottobre 2015

- Corso di Analisi
--Teoria dei Limiti
Settembre 2015

- Corso di Analisi
-- Spazi Metrici
Agosto 2015

- Corso di Analisi
-- Numeri Complessi
Luglio 2015

- Corso di Analisi
-- Numeri Reali
Giugno 2015

- Integrali Impropri
Maggio 2015

- Funzioni Analitiche II
Aprile 2015

- Funzioni Analitiche I
Marzo 2015

- Integrale Teoria Generale II
Febbraio 2015

- Integrale Teoria Generale I
Gennaio 2015

- Derivate di ordine superiore
Dicembre 2014

- Derivata teoria generale.
Novembre 2014

- Serie teoria generale.-
Ottobre 2014

- Limiti teoria generale II
Settembre 2014

- Limiti teoria generale I
Agosto 2014

- Spazi Metrici.
Luglio 2014

– Funzioni Reali II
Giugno 2014

- Funzioni Reali I
Maggio 2014

- Disequazioni Trascendenti -
Aprile 2014

– Disequazioni
Marzo 2014

- Fascio di Coniche II
Febbraio 2014

- Fascio di Coniche I
Gennaio 2014

– Geometria Analitica I
Dicembre 2013

– Trigonometria
Novembre 2013

– Metodo di Tartenville
Ottobre 2013

- Dimostrazione Formale
Settembre 2013

– Logica Matematica
Agosto 2013

– Insiemi
Luglio 2013

- Logica
Giugno 2013

- Analisi Matematica II
Maggio 2013

– Metrica Euclidea
Aprile 2013

– Derivazione
Marzo 2013

– Elementi di Topologia
Febbraio 2013

- Le Serie
Gennaio 2013

– Teoria degli Insiemi
Dicembre 2012

– Teoria degli Insiemi
Novembre 2012

– Teoria degli Insiemi
Ottobre 2012

– Teoria degli Insiemi
Settembre 2012

– Teoria degli Insiemi
Agosto 2012

– Teoria degli Insiemi
Luglio 2012

– Teoria degli Insiemi
Giugno 2012

– Teoria degli Insiemi
Maggio 2012

– Teoria degli Insiemi
Aprile 2012

– Teoria degli Insiemi
Marzo 2012

– Teoria degli Insiemi
Febbraio 2012

– Teoria degli Insiemi
Gennaio 2012

– Teoria degli Insiemi
Dicembre 2011

– Teoria degli Insiemi
Novembre 2011

– Teoria degli Insiemi
Ottobre 2011

– Teoria degli Insiemi
Settembre 2011

– Teoria degli Insiemi
Agosto 2011

– Teoria degli Insiemi
Luglio 2011

– Teoria degli Insiemi
Giugno 2011

– Teoria degli Insiemi
Maggio 2011

– Teoria degli Insiemi
Aprile 2011

– Teoria degli Insiemi
Marzo 2011

– Teoria degli Insiemi
Febbraio 2011

– Teoria degli Insiemi
Gennaio 2011

– Teoria degli Insiemi
Dicembre 2010

– Teoria degli Insiemi
Tag
Applicazioni del piano complesso in se stesso Condizione Sufficiente coordinate polari Criteri di convergenza per serie a termini non negativi Criterio di Cauchy Definizione di derivata DERIVATE DI ORDINE SUPERIORE Differenziale dominio di una funzione equazione differenziale Equazione di Laplace Equazioni e Disequazioni Trascendenti formula di Taylor funzione arcocosecante funzione arcocoseno funzione arcosecante funzione arcoseno funzione armonica funzione biunivoca Funzione concava Funzione convessa funzione esponenziale Funzione Iniettiva Funzione inversa funzione periodica Funzione ricorsiva funzione suriettiva Funzione Trigonometriche funzioni discontinue funzioni trigonometriche grafico di una funzione gruppo identità di Eulero Il Pensiero Matematico Insieme aperto Insieme chiuso Integrale di Lebesgue integrale di riemann Integrali curvilinei di funzioni complesse Integrali impropri contenenti un parametro integrazione per parti isometria Le Coniche Limite (+) infinito per x che tende a un valore (+) infinito limite di una funzione Limite di una Serie numerica con Excel Limiti Limiti calcolo mediante limiti notevoli matrici Numeri Complessi Numeri Reali Permutazione Polinomi polinomi a coefficienti reali Polinomio di Taylor Problema di Cauchy prodotto scalare prodotto vettoriale Punti singolari isolati punto di accumulazione punto isolato Radice ennesima di x∈R x≧0 regole di derivazione Schema generale di applicazione dell'integrale Serie Armonica Serie di Taylor simmetria assiale Spazio Metrico Completo teorema di Cauchy teorema di Lagrange teorema di Rolle trasformazioni lineari trigonometria vettori vettori linearmente dipendenti
Instagram
Amministrazione
- Registrati
- Accedi
- Flusso di pubblicazione
- Feed dei commenti
- WordPress.com
e-mail

Inserisci il tuo indirizzo e-mail per iscriverti a questo blog e ricevere notifiche di nuovi messaggi per e-mail.

Indirizzo email:

Unisciti a 235 altri iscritti
Vivi l’Attimo!
Articoli e Pagine
- FUNZIONE ARMONICA
- Densità di ℚ in ℝ
- Cambio di variabile per gli integrali doppi : Lezione 20
- La serie armonica generalizzata
- Serie geometrica
- Quadrica: Ellissoide
- Permutazioni pari e dispari
- Teorema dei valori intermedi
- Limite infinito per x tendente a un valore finito
- teorema dei moltiplicatori di Lagrange in tre variabili : Lezione 16
Autore
Social
- Visualizza il profilo di sdlrmr@gmail.com su Facebook
- Visualizza il profilo di rmr4448 su Twitter
- Visualizza il profilo di rmr4448 su Instagram
- Visualizza il profilo di salvatore-di-lucia-a52302b8 su LinkedIn
- Google+

iMathematica

punto singolare di una curva

°°°°°

“La matematica non conosce razze o confini geografici; per la matematica, il mondo culturale è una singola nazione.”

°°°°°

punto singolare di una curva

In geometria,

un punto singolare di una curva è un punto per il quale la curva non è rappresentata da una funzione liscia.

La definizione precisa dipende dal tipo di curva che si considera.

Curve algebriche nel piano

Una curva algebrica nel piano è definita come il luogo geometrico dei punti del piano che soddisfano una equazione nella forma dove

è una funzione polinomiale

Se l’origine appartiene alla curva allora . Se allora il teorema delle funzioni implicite assicura che esiste una funzione liscia tale che la curva ha la forma in un intorno dell’origine.

Analogamente, se allora esiste una funzione liscia tale che la curva ha la forma in un intorno dell’origine.

In entrambi i casi, esiste una mappa regolare da al piano sul quale è definita la curva in un intorno dell’origine.

Nell’origine si ha che

per cui la curva è non singolare, o regolare, nell’origine se almeno una delle derivate parziali di è non nulla.

I punti singolari sono quei punti della curva nei quali si annulla il gradiente di :

Punti di regolarità

Assumendo che la curva passi per l’origine e ponendo , può essere scritta come

Se allora ha una soluzione di molteplicità per e l’origine è un punto di contatto di ordine con la retta .

Se allora ha una soluzione di molteplicità maggiore o uguale a e la retta ovvero è tangente alla curva. In tale caso, se allora la curva ha un punto di contatto di ordine con .

Se il coefficiente di è nullo ovvero se ma non è nullo il coefficiente di allora l’origine è un punto di flesso della curva.

Se entrambi i coefficienti di e sono nulli allora l’origine è un punto di ondulazione.

Tale analisi si generalizza ad ogni punto della curva, traslandola in modo che il punto di interesse vada a cadere nell’origine.

Punti doppi

Tre limaçon:

la curva a sinistra ha un punto doppio isolato nell’origine,

quella al centro (cardioide) ha una cuspide nell’origine,

quella a destra ha un nodo (autointersezione) nell’origine.

Se e sono entrambi nulli ma almeno uno tra , e è non nullo allora l’origine è un punto doppio per la curva.

Ponendo , può essere scritta come

I punti doppi possono essere classificati secondo le soluzioni di .

Nodi

Se ha due soluzioni reali rispetto a , ovvero se allora l’origine è un nodo per la curva.

In tale caso la curva ha un’autointersezione nell’origine e ha due tangenti distinte corrispondenti alle due soluzioni di .

La funzione ha un punto di sella in corrispondenza.

Punti doppi isolati

Se non ha soluzioni reali rispetto a , ovvero se , allora l’origine è un punto doppio isolato (o nodo isolato).

Nel piano reale è quindi un punto isolato, ma se si considera la curva complessa l’origine non è un punto isolato e ha due tangenti immaginarie, corrispondenti alle due soluzioni complesse di .

La funzione ha un estremo locale in corrispondenza.

Cuspidi

Se

ha una soluzione di molteplicità rispetto a , ovvero

allora l’origine è un punto di cuspide.

La curva cambia direzione con un angolo netto nell’origine e ha una sola tangente, che può essere considerata come due tangenti coincidenti.

Ulteriori classificazioni

Il numero di nodi o cuspidi di una curva è uno dei due invarianti della formula di Plücker.

Se una delle soluzioni di

è anche soluzione di

allora il ramo corrispondente della curva ha un punto di flesso nell’origine, che in questo caso è un punto di flencnodo.

Se entrambe le tangenti hanno questa proprietà, ovvero

è un fattore di

allora l’origine è un biflecnodo.

Punti multipli

La curva ha un punto triplo nell’origine

In generale, se tutti i termini di grado inferiore a sono nulli, almeno un termine di grado è non nullo in e la curva ha un punto multiplo di ordine .

La curva avrà, in generale, tangenti nell’origine, anche se alcune di esse possono essere immaginarie.

Curve parametriche

Una curva parametrica in è definita come l’immagine di una funzione

I punti singolari sono quelli per i quali si annulla il gradiente di , ovvero

Molte curve possono essere definite in questa maniera, ma le definizioni di singolarità possono non essere sempre concordi.

La cuspide è singolare in entrambe le definizioni, un esempio è la curva seguente che ha una cuspide nell’origine, e può essere definita implicitamente come

o in forma parametrica come

Nel caso dei nodi non è sempre questo il caso, ad esempio nella curva

l’origine è un punto singolare se si considera la curva definita implicitamente in forma algebrica, ma considerando la parametrizzazione

si ha che

non si annulla mai, e il nodo non è un punto singolare per la parametrizzazione.

È necessario prestare attenzione nella scelta della parametrizzazione:

ad esempio la retta parametrizzata da

ha una singolarità nell’origine, mentre quando è parametrizzata da non ha singolarità.

Per questo motivo, è più opportuno parlare di punto singolare di una parametrizzazione regolare piuttosto che di punto singolare della curva in sé.

La precedente definizione può essere estesa per coprire i punti singolari delle curve implicite, che sono definiti come insieme degli zeri di una funzione liscia, e può essere estesa per curve in più dimensioni.

Un teorema di Hassler Whitney afferma che ogni insieme chiuso in è l’insieme degli zeri

di una opportuna funzione liscia

.

°°°°°

Segue …

Funzione liscia

Funzioni lisce e funzioni analitiche nel caso reale

Una curva algebrica nel piano è definita come il luogo geometrico dei punti $(x,y)$ del piano che soddisfano una equazione nella forma $f(x,y)=0$ dove

$f$ è una funzione polinomiale $f\colon \mathbb{R} ^{2}\to \mathbb{R}$

Se l’origine $(0,0)$ appartiene alla curva allora $a_{0}=0$ . Se $b_{1}\neq 0$ allora il teorema delle funzioni implicite assicura che esiste una funzione liscia $h$ tale che la curva ha la forma $y=h(x)$ in un intorno dell’origine.

Analogamente, se $b_{0}\neq 0$ allora esiste una funzione liscia $k$ tale che la curva ha la forma $x=k(y)$ in un intorno dell’origine.

In entrambi i casi, esiste una mappa regolare da $\R$ al piano sul quale è definita la curva in un intorno dell’origine.

per cui la curva è non singolare, o regolare, nell’origine se almeno una delle derivate parziali di $f$ è non nulla.

I punti singolari sono quei punti della curva nei quali si annulla il gradiente di $f$ :

Assumendo che la curva passi per l’origine e ponendo $y = mx$ , $f$ può essere scritta come

Se $b_{0}+mb_{1}\neq 0$ allora $f=0$ ha una soluzione di molteplicità $1$ per $x=0$ e l’origine è un punto di contatto di ordine $1$ con la retta $y = mx$ .

Se $b_{0}+mb_{1}=0$ allora $f=0$ ha una soluzione di molteplicità maggiore o uguale a $2$ e la retta $y = mx$ ovvero $b_{0}x+b_{1}y=0$ è tangente alla curva. In tale caso, se $c_{0}+2mc_{1}+c_{2}m^{2}\neq 0$ allora la curva ha un punto di contatto di ordine $2$ con $y = mx$ .

Se il coefficiente di ${\displaystyle x^{2))$ è nullo ovvero se $c_{0}+2mc_{1}+c_{2}m^{2}=0$ ma non è nullo il coefficiente di $x^3$ allora l’origine è un punto di flesso della curva.

Se entrambi i coefficienti di ${\displaystyle x^{2))$ e $x^3$ sono nulli allora l’origine è un punto di ondulazione.

Se ${\displaystyle b_{0))$ e ${\displaystyle b_{1))$ sono entrambi nulli ma almeno uno tra ${\displaystyle c_{0))$ , ${\displaystyle c_{1))$ e ${\displaystyle c_{2))$ è non nullo allora l’origine è un punto doppio per la curva.

Ponendo $y = mx$ , $f$ può essere scritta come

I punti doppi possono essere classificati secondo le soluzioni di $c_{0}+2mc_{1}+c_{2}m^{2}=0$ .

Se $c_{0}+2mc_{1}+c_{2}m^{2}=0$ ha due soluzioni reali rispetto a $m$ , ovvero se $c_{0}c_{2}-(c_{1})^{2}<0$ allora l’origine è un nodo per la curva.

In tale caso la curva ha un’autointersezione nell’origine e ha due tangenti distinte corrispondenti alle due soluzioni di $c_{0}+2mc_{1}+c_{2}m^{2}=0$ .

La funzione $f$ ha un punto di sella in corrispondenza.

Se $c_{0}+2mc_{1}+c_{2}m^{2}=0$ non ha soluzioni reali rispetto a $m$ , ovvero se $c_{0}c_{2}-(c_{1})^{2}>0$ , allora l’origine è un punto doppio isolato (o nodo isolato).

Nel piano reale è quindi un punto isolato, ma se si considera la curva complessa l’origine non è un punto isolato e ha due tangenti immaginarie, corrispondenti alle due soluzioni complesse di $c_{0}+2mc_{1}+c_{2}m^{2}=0$ .

La funzione $f$ ha un estremo locale in corrispondenza.

Se $c_{0}+2mc_{1}+c_{2}m^{2}=0$

ha una soluzione di molteplicità $2$ rispetto a $m$ , ovvero

$c_{0}+2mc_{1}+c_{2}m^{2}=0$ è un fattore di

La curva $f(t)=(\sin(2t)+\cos(t),\sin(t)+\cos(2t)$ ha un punto triplo nell’origine

In generale, se tutti i termini di grado inferiore a $k$ sono nulli, almeno un termine di grado $k$ è non nullo in $f$ e la curva ha un punto multiplo di ordine $k$ .

La curva avrà, in generale, $k$ tangenti nell’origine, anche se alcune di esse possono essere immaginarie.

Una curva parametrica in $\R^2$ è definita come l’immagine di una funzione

I punti singolari sono quelli per i quali si annulla il gradiente di $g$ , ovvero

ad esempio la retta $y=0$ parametrizzata da

ha una singolarità nell’origine, mentre quando è parametrizzata da $g(t)=(t,0)$ non ha singolarità.

La precedente definizione può essere estesa per coprire i punti singolari delle curve implicite, che sono definiti come insieme degli zeri $f^((-1))(0)$ di una funzione liscia, e può essere estesa per curve in più dimensioni.

Un teorema di Hassler Whitney afferma che ogni insieme chiuso in $\mathbb {R} ^{n}$ è l’insieme degli zeri

$f\colon \mathbb{R} ^{n}\to \mathbb{R}$ .

Siano $M$ e $N$ varietà differenziabili e $p$ un punto di $M$ . Una funzione $F:M\rightarrow N$ è detta differenziabile in $p$ (oppure liscia o di classe $C^\infty$ in $p$ ) se esistono una carta $(U,\phi )$ in $p$ ed una carta $(V,\psi )$ in $F(p)$ tali che $F(U)\subset V$ e la composizione:

sia liscia in un intorno di $\phi (p)$ . Tale definizione non dipende dalle carte scelte: prendendo infatti altre carte $(U',\phi ')$ e $(V',\phi ')$ la composizione $\psi '\circ \ F\circ \phi '^((-1))$ rimane liscia in un intorno di $\phi (p)$ .

$F$ è differenziabile (liscia, di classe $C^\infty$ ) se lo è per ogni $p$ in $M$ . Se inoltre $F$ è invertibile con inversa liscia allora $F$ si dirà un diffeomorfismo. Lo studio delle proprietà invarianti per diffeomorfismi è oggetto della topologia differenziale.

Una funzione $f$ è analitica su un insieme aperto $D$ della retta reale se per ogni $x_0$ in $D$ si può scrivere $f(x)$ come:

dove i coefficienti $a_{0},a_{1},\cdots$ sono numeri reali e la serie è convergente in un intorno di $x_0$ .

in ogni punto $x_0$ appartenente al dominio, converge a $f(x)$ per $x$ in un intorno di $x_0$ .

L’insieme di tutte le funzioni analitiche reali appartenenti ad un dato insieme $D$ si denota di solito come $C^\omega(D)$ .

Una funzione $f$ definita in un qualche sottoinsieme della retta reale, si dice essere reale analitica al punto $x$ se esiste un intorno $D$ di $x$ nel quale $f$ è reale analitica.

è liscia in $x=0$ ma non è analitica in 0.

Formalmente, sia $f : (a,b) \to \mathbb{R}$ ed appartenente a $C^{\infty}(a,b)$ e sia $x_0 \in (a,b)$ .

Se esistono $\Lambda, M, \delta > 0$ tali che:

In particolare, se una funzione ha tutte le derivate limitate da una stessa costante $\Lambda$ su un intervallo, allora è ivi analitica (basta porre $M = 1$ nell’enunciato precedente).

Dato che la funzione $f$ è liscia, è possibile scriverne la formula di Taylor arrestata all’ordine $n - 1$ (resto secondo Lagrange):

Se $x$ si muove nell’intorno di $x_0$ di raggio $\delta$ si può usare la maggiorazione (in valore assoluto) garantita dall’ipotesi:

cioè la serie converge puntualmente a $f$ sull’intervallo $(x_0 - \delta, x_0 + \delta)$ ,