RSS

Semicontinuità

13 Apr

Semicontinuità

In analisi matematica,

la semicontinuità di una funzione reale è una proprietà più debole della continuità.

Intuitivamente,

se una funzione continua in un punto è localmente limitata, una funzione semicontinua inferiormente (o superiormente) in un punto sarà localmente solo limitata inferiormente (o superiormente).

La definizione di semicontinuità, come quella di continuità, si può porre anche in uno spazio astratto come uno spazio topologico.

Definizione

$Funzione semicontinua inferiormente. Essa non è semicontinua superiormente poiché il suo massimo limite in x 0 {\displaystyle x_{0)) è uguale al limite destro$

Funzione semicontinua inferiormente.

Essa non è semicontinua superiormente poiché il suo massimo limite in $x_0$ è uguale al limite destro

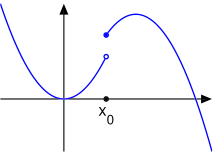
Funzione semicontinua superiormente

Funzione semicontinua superiormente

In uno spazio topologico

Una funzione $f:X\to \mathbb {R}$ si dice semicontinua inferiormente(s.c.i.) in $x_0$ se per ogni $\varepsilon >0$ esiste un intorno $U(x_{0})$ tale che:

$f(x)>f(x_{0})-\varepsilon \$

per ogni $x$ in $U(x_{0})$ .

Equivalentemente,

Una funzione $f:X\to \mathbb {R}$ definita in uno spazio topologico si dice semicontinua inferiormente in $x_0$ se:

\liminf _{x\to x_{0))f(x)\geq f(x_{0})

dove $\liminf$ è il limite inferiore di $f$ in $x_0$ .

Una funzione semicontinua inferiormente ha dunque tutte le immagini definitamente sopra o vicino al valore $f(x_0)$ .

°°°°°

Una funzione $f:X\to \mathbb {R}$ si dice semicontinua superiormente in $x_0$ (s.c.s.) se per ogni $\varepsilon >0$ esiste un intorno $U(x_{0})$ tale che:

f(x)<f(x_{0})+\varepsilon \

per ogni $x$ in $U(x_{0})$ .

Equivalentemente,

Una funzione $f:X\to \mathbb {R}$ si dice semicontinua superiormente in $x_0$ se:

\limsup _{x\to x_{0))f(x)\leq f(x_{0})

dove $\limsup$ è il limite superiore di $f$ in $x_0$ .

Una funzione semicontinua superiormente ha dunque tutte le immagini definitamente sotto o vicino al valore $f(x_0)$ .

°°°°°

Esempi

La funzione parte intera, $f(x)=\lfloor x\rfloor$ è semicontinua superiormente.
La funzione parte intera superiore $f(x)=\lceil x\rceil$ è semicontinua inferiormente.
La funzione di Dirichlet $f(x)=\left\((\begin{matrix}1&x\in \mathbb {Q} \\0&x\in \mathbb {R} -\mathbb {Q} \end{matrix))\right.$ è
semicontinua inferiormente in ogni punto irrazionale

e

semicontinua superiormente in ogni punto razionale.

La funzione indicatrice di un insieme aperto è semicontinua inferiormente;

La funzione indicatrice di un insieme chiuso è semicontinua superiormente

°°°°°

Parte intera

In matematica,

la funzione parte intera, nota anche come funzione floor (dalla parola inglese floor che significa “pavimento”), è la funzione che associa ad ogni numero reale $x$ il più grande intero minore o uguale a $x$ . La funzione parte intera è solitamente indicata con $\lfloor x\rfloor$ o $[x]$ .

La funzione mantissa, definita come $x-\lfloor x\rfloor$ , anche scritta come $x$ mod 1, oppure $\{x\}$ , è chiamata la parte frazionaria di $x$ . Ogni frazione $x$ può essere scritta come un numero misto, cioè la somma di un intero e una frazione propria. La funzione floor e la funzione parte frazionaria estendono questa decomposizione a tutti i numeri reali.

Proprietà

Qualche proprietà della funzione parte intera

Si ha

$\lfloor x\rfloor =\max \,\{k\in {\mathbb {Z)):k\leq x\}$

$\lfloor x\rfloor \leq x<\lfloor x\rfloor +1$

con l’uguaglianza nella parte sinistra che vale se e solo se $x$ è un intero.

La funzione parte intera è idempotente:

$\lfloor \lfloor x\rfloor \rfloor =\lfloor x\rfloor$ .

Per ogni intero $k$ e ogni numero reale $x$ ,

$\lfloor k+x\rfloor =k+\lfloor x\rfloor .$

Per ogni numero reale non intero $x$ si ha:

\lfloor -x\rfloor =-\lfloor x\rfloor -1,

L’ordinario arrotondamento di un numero $x$ all’intero più vicino può essere espresso come $\lfloor x+0,5\rfloor$ .
La funzione parte intera non è continua, ma è semi-continua. Essendo una funzione costante a tratti , la sua derivata è zero quando esiste, cioè per tutti i valori che non sono interi.
Se $x$ è un numero reale e $n$ un intero, si ha $n\leq x$ se e solo se $n\leq \lfloor x\rfloor .$ In linguaggio ricercato, la funzione parte intera fa parte di una connessione di Galois; è l’aggiunta superiore della funzione che immerge gli interi nei reali.
Usando la funzione floor, si possono produrre diverse formule per calcolare i numeri primi che sono esplicite ma non utilizzabili nella pratica.
Il teorema di Beatty afferma che ogni numero irrazionale partiziona i numeri naturali in due sequenze tramite la funzione floor.

Parte intera superiore

La funzione ceiling

La funzione ceiling

Una funzione strettamente correlata è la parte intera superiore, nota anche come funzione ceiling (dalla parola inglese ceiling che significa “soffitto”, contrapposta a floor, “pavimento”), definita nel modo seguente: per ogni numero reale $x$ , ceiling( $x$ ) è il più piccolo intero non minore di $x$ . Per esempio, ceiling(2,3) = 3, ceiling(2) = 2 e ceiling(−2,3) = −2. La funzione ceiling è anche indicata con $\lceil x\rceil$ . È facile provare che

\lceil x\rceil =-\lfloor -x\rfloor

e che

$x\leq \lceil x\rceil <x+1$

Se poi x non è un intero si ha

$\lceil x\rceil -\lfloor x\rfloor =1$

Per ogni intero k, abbiamo anche che:

$\lfloor k/2\rfloor +\lceil k/2\rceil =k$ .

Se m e n sono interi positivi primi fra di loro, allora

\sum _((i=1))^((n-1))\lfloor im/n\rfloor =(m-1)(n-1)/2

In programmazione

L'operatore (int)

L’operatore (int)

In C

Praticamente tutti i linguaggi di programmazione forniscono al programmatore la possibilità di convertire un valore di un certo tipo di dato in un valore di un altro tipo. Nello specifico, questo rende possibile convertire valori decimali (che vengono tipicamente rappresentati in virgola mobile) in numeri interi (di solito rappresentato come complemento a due).

Nel linguaggio di programmazione C, questo è reso possibile dall’operatore di casting `(int)`. Questa operazione è un misto delle funzioni floor e ceiling: per x positivi o nulli, restituisce floor(x), e per x negativi restituisce ceiling(x).

La stessa sintassi funziona con numerosi altri linguaggi, soprattutto quelli derivati dal C, come Java e Perl, così come la funzione POSIX floor().

Problemi di arrotondamento

L’uso dell’arrotondamento può generare effetti imprevisti e che vanno contro quello che l’intuito suggerirebbe. Per esempio, `(int)(0,6/0,2)` restituisce il valore 2 nella maggior parte delle implementazioni del C, anche se matematicamente è 0,6/0,2 = 3.

Questo problema è dovuto al fatto che i computer lavorano internamente con il sistema numerico binario e non è possibile rappresentare i numeri 0,6 e 0,2 con stringhe binarie di lunghezza finita. Più in generale: i computer non lavorano mai direttamente con un certo numero decimale, ma solo con una sua approssimazione. Nell’esempio, quindi, il risultato viene calcolato come 2,999999999999999555910790149937, che l’operatore `(int)` converte tranquillamente al valore 2.

A causa di questi problemi, la maggior parte delle calcolatrici moderne usa internamente il sistema numerico decimale codificato in binario.

Distribuzione uniforme modulo 1

Se $x$ è un numero irrazionale, allora le parti frazionarie $nx{\bmod {1))$ , dove $n$ varia fra gli interi positivi, sono distribuite uniformemente nell’intervallo aperto $(0,1)$ . Questa affermazione può essere resa più precisamente in molti modi, uno dei quali afferma:

$\int _{0}^{1}f(t)\;dt=\lim _{N\to \infty }{\frac {1}{N))\sum _{n=1}^{N}f(nx{\bmod {1))),$

per ogni funzione continua a valori reali $f\colon [0,1]\to \mathbb {R}$ (vedi limite, integrale e teorema dell’equidistribuzione).

Seguendo il principio generale dell’approssimazione diofantea scoperto da Hermann Weyl, questa proprietà è equivalente a qualcosa che è molto più facile da controllare: ossia che le somme

$\sum \limits _{n=0}^{N}e^{2\pi iknx},$

per $k\in {\mathbb {N))$ sono O(N). Poiché sono progressioni geometriche, questo può essere provato in maniera abbastanza diretta. La condizione che $x$ sia irrazionale implica che

$\sin \pi kx\neq 0.$

Troncamento

Troncamento (matematica).

Mentre la funzione parte intera genera solamente numeri interi, il troncamento, cioè il “tagliare fuori le cifre”, può essere effettuato a qualsiasi posizione specificata, non solo dopo la cifra delle unità.

Notazione

Le funzioni parte intera superiore e inferiore sono normalmente indicate con parentesi quadre, chiuse e aperte, in cui le linee orizzontali superiori (per la funzione parte intera inferiore, floor) o inferiori (per la funzione parte intera superiore, ceiling) sono mancanti. Per esempio nel sistema di composizione editoriale LaTeX questi simboli possono essere realizzati con i comandi \lfloor, \rfloor, \lceil e \rceil.

°°°°°

Funzione di Dirichlet

La funzione di Dirichlet è una funzione di variabile reale, che assume due soli valori, diversi a seconda che la variabile indipendente sia razionale o irrazionale. Questa funzione fu introdotta da Peter Dirichlet come esempio di funzione molto lontana dalle tradizionali funzioni note fino ad allora nell’analisi matematica.

Definizione

La funzione di Dirichlet è definita nel modo seguente:

\chi (x)={\begin{cases}1&x\in {\mathbb {Q))\\0&x\in {\mathbb {R))\setminus {\mathbb {Q))\end{cases))

È la funzione indicatrice dell’insieme dei razionali $\mathbb{Q}$ . Viene talora chiamata funzione di Dirichlet la funzione definita a valori invertiti:

\chi (x)={\begin{cases}0&x\in {\mathbb {Q))\\1&x\in {\mathbb {R))\setminus {\mathbb {Q))\end{cases))

Nel seguito quest’ultima funzione sarà indicata come $1-\chi$ .

Continuità e integrabilità

La funzione di Dirichlet è un esempio di funzione che non è continua in nessun punto del dominio, infatti ogni intorno di qualsiasi punto contiene sempre almeno un numero razionale e un numero irrazionale (in effetti infiniti punti per entrambe le categorie) e quindi due punti in cui la funzione assume valore 0 e 1.

La funzione è non integrabile secondo Riemann ma integrabile secondo Lebesgue.

Poiché la funzione assume quasi ovunque valore 0 (essendo l’insieme dei numeri razionali un insieme di misura nulla poiché l’insieme dei numeri razionali è numerabile, mentre gli irrazionali non lo sono) il risultato dell’operazione di integrazione su qualunque intervallo $[a,b]$ è 0.

Per analoghe ragioni, l’integrale della funzione $1-\chi$ sull’intervallo $[a,b]$ vale $b-a$ .

Altre proprietà

Il grafico della funzione apparirebbe come due rette orizzontali, di ordinata 0 e 1, “sbiadite”, ovvero fatte di tanti punti infinitamente vicini e “buchi” puntiformi infinitamente vicini.

La funzione di Dirichlet è approssimabile mediante funzioni continue secondo la formula seguente:

\chi (x)=\lim _((n\rightarrow \infty ))\lim _((m\rightarrow \infty ))\left[\cos \left(2\pi n!x\right)\right]^{m}

La funzione $1-\chi$ presenta inoltre un minimo relativo e assoluto improprio per ogni x razionale, ed un massimo relativo e assoluto improprio per ogni x irrazionale.

Funzione di Dirichlet modificata

Lo stesso argomento in dettaglio: Funzione di Thomae.

Nel 1854 Bernhard Riemann descrisse una variante (detta anche funzione di Thomae) della funzione di Dirichlet, che pur essendo discontinua su ogni intervallo della retta reale, è integrabile secondo Riemann. Una possibile definizione di questa funzione è:

\mathrm{X} (x)={\begin{cases}{\frac {1}{q))&x={\frac {p}{q)),{\mbox{con )){\frac {p}{q)){\mbox{ ridotta ai minimi termini))\\0&x\in {\mathbb {R))\setminus {\mathbb {Q)).\end{cases))

Questa funzione è integrabile secondo Riemann perché dato un qualunque valore positivo $\varepsilon$ , la funzione supera $\varepsilon$ solamente in un numero finito di punti; le somme integrali che approssimano il valore dell’integrale tendono quindi a zero.

Inoltre, la funzione è anche continua in ogni valore irrazionale di $x$ : preso infatti un numero irrazionale $x_0$ e fissato un valore positivo $\varepsilon$ , esiste sempre un intorno di $x_0$ in cui $\mathrm{X} (x_{0})<\varepsilon$ ; segue quindi che:

$\lim _((x\rightarrow x_{0))}\mathrm{X} (x)=0$

°°°°°

Funzione indicatrice

In matematica, nel campo della teoria degli insiemi,

se $A$ è un sottoinsieme dell’insieme $X$ , la funzione indicatrice, o funzione caratteristica di $A$ è quella funzione da $X$ all’insieme $\{0,1\}$ che sull’elemento $x\in X$ vale $1$ se $x$ appartiene ad $A,$ e vale $0$ in caso contrario.

Definizione

La funzione indicatrice di un sottoinsieme $A$ di $X$ è una funzione

{\mathbf {1))_{A}:X\to \lbrace 0,1\rbrace

definita come

{\mathbf {1))_{A}(x)=\left\((\begin{matrix}1&{\mbox{se))\ x\in A\\0&{\mbox{se))\ x\notin A\end{matrix))\right.

La funzione indicatrice di $A$ è talvolta indicata con $\chi _{A}(x)$ oppure $I_{A}(x).$

Proprietà fondamentali

La funzione che associa un sottoinsieme $A$ di $X$ alla sua funzione indicatrice ${\displaystyle \mathbf {1} _{A))$ è iniettiva;

il suo codominio è l’insieme delle funzioni $\mathbf {f} \colon X\to \{0,1\}.$

Se $A$ e $B$ sono due sottoinsiemi di $X,$ allora

{\mathbf {1))_((A\cap B))=\min\((\mathbf {1))_{A},{\mathbf {1))_{B}\}={\mathbf {1))_{A}{\mathbf {1))_{B}\qquad {\mbox{e))\qquad {\mathbf {1))_((A\cup B))=\max\(({\mathbf {1))_{A},{\mathbf {1))_{B))\}={\mathbf {1))_{A}+{\mathbf {1))_{B}-{\mathbf {1))_{A}{\mathbf {1))_{B}.

Più in generale,

supponiamo che $A_{1},\ldots ,A_{n}$ sia una collezione di sottoinsiemi di $X.$

Per ogni $x\in X$ si ha che il prodotto

\prod _{k=1}^{n}(1-\mathbf {1} _{A_{k))(x))

è chiaramente un prodotto di $0$ e $1.$

Questo prodotto ha il valore $1$ proprio in corrispondenza degli $x\in X$ che non appartengono a nessuno degli insiemi $A_{k}$ ed è $0$ altrove.

Cioè

\prod _{k=1}^{n}(1-\mathbf {1} _{A_{k)))=\mathbf {1} _{X-\bigcup _{k}A_{k))=1-\mathbf {1} _{\bigcup _{k}A_{k)).

Sviluppando il prodotto a destra e a sinistra,

\mathbf {1} _{\bigcup _{k}A_{k))=1-\sum _{F\subseteq \{1,2,\ldots ,n\))(-1)^{|F|}\mathbf {1} _{\bigcap _{F}A_{k))=\sum _{\varnothing \neq F\subseteq \{1,2,\ldots ,n\))(-1)^{|F|+1}\mathbf {1} _{\bigcap _{F}A_{k))

Dove $|F|$ è la cardinalità di $F.$

Questa è una delle forme del principio di inclusione-esclusione.

Come suggerito dal precedente esempio, la funzione indicatrice è uno strumento utile nella combinatoria.

La notazione è usata in altri casi,

ad esempio

in teoria della probabilità:

se $X$ è uno spazio di probabilità con misura di probabilità $P$ e $A$ è un insieme misurabile, allora ${\displaystyle \mathbf {1} _{A))$ diventa una variabile casuale la cui media è uguale alla probabilità di $A:$

E(\mathbf {1} _{A})=\int _{X}\mathbf {1} _{A}(x)\,dP=\int _{A}dP=P(A).

Questa identità è usata in una dimostrazione semplice della disuguaglianza di Markov.

Se $A$ è l’insieme di tutti i numeri positivi di $X$ compreso lo zero se ne è incluso allora si può scrivere

\mathbf {1} _{A}(x)=\mathbf {1} _{X^{+))(x)=\mathrm {sgn} \left(\mathrm {sgn} (x)+1\right).

Analisi convessa

In analisi convessa, una branca dell’analisi matematica che studia funzioni e insiemi convessi, spesso con applicazioni alla teoria dell’ottimizzazione, si utilizza un’altra definizione di funzione indicatrice, che si rivela più utile per gli strumenti della disciplina: una funzione indicatrice è qui rappresentata da una

$\chi _{A}:X\to \mathbb{R} \cup \{-\infty ,+\infty \}$ tale che

\chi _((A))(x):={\begin{cases}0,&x\in A;\\+\infty ,&x\not \in A.\end{cases))

Rispetto alla funzione indicatrice prima definita ha questo rapporto:

{\mathbf {1))_((A))(x)={\frac {1}{1+\chi _((A))(x)))

e

\chi _((A))(x)=(+\infty )\left(1-{\mathbf {1))_((A))(x)\right)

relazioni valide ponendo per convenzione ${1 \over 0}=+\infty$ e ${1 \over +\infty }=0$

°°°°°

Proprietà

Una funzione è continua se e solo se è

sia semicontinua inferiormente

sia semicontinua superiormente.

Una funzione semicontinua inferiormente in un insieme compatto ammette minimo.

Analogamente,

una funzione semicontinua superiormente in un insieme compatto ammette massimo.

Se $f$ e $g$ sono semicontinue superiormente allora lo è anche $f+g$ , e se entrambe sono non negative anche $fg$ .
Inoltre, se $f$ è semicontinua superiormente, allora $kf$ (con $k$ < 0) è semicontinua inferiormente.

Una funzione è semicontinua inferiormente se e solo se esiste una successione di funzioni gradino ${\displaystyle (g_{n})_{n\in \mathbb {N} ))$ tale che:

$g_{n}$ è semicontinua inferiormente per ogni $n$ ;
$g_{n}(x)\leq g_{n+1}(x)$ per ogni $n$ e $x$ ;
$\lim _{n\to \infty }g_{n}(x)=f(x)$ , cioè $g_{n}$ converge puntualmente a $f$ .

Se ${\displaystyle (f_{i})_{i\in I))$ è una successione di funzioni semicontinue inferiormente, allora la funzione definita come $f(x)=\sup _{i\in I}f_{i}(x)$ è semicontinua inferiormente.

L’inviluppo inferiore $f_{*}$ di una qualsiasi funzione è semicontinuo superiormente; si ha che $f$ è semicontinua superiormente se e solo se ${\displaystyle f=f_{*))$ .

°°°°°

Segue …

Disuguaglianza di Markov

In teoria della probabilità e statistica,

la disuguaglianza di Markov afferma che, per una variabile casuale $X$ non negativa il cui valore atteso esiste:

P\left(X\geq \alpha \right)\leq {\frac {\mathbb {E} [X]}{\alpha ))

Questa disuguaglianza permette di stabilire un limite superiore al valore di probabilità dalla sola conoscenza del valore atteso $\mathbb {E} [x],$ a condizione che la variabile casuale sia definita non negativa.

La disuguaglianza di Markov è anche utilizzata nella dimostrazione della disuguaglianza di Čebyšëv.

Dimostrazione

Si definiscano le variabili casuali $X$ ed $I$ come segue:

X:\Omega \rightarrow \mathbb {R} _{0}^{+},

con $\Omega$ spazio campionario e

\ I=\left\((\begin{matrix}1&\iff &X\geq \alpha \\0&\iff &X<\alpha \end{matrix))\right.

con $\alpha \in \mathbb {R} ^{+}.$

Chiaramente per ogni $\alpha$ non nullo, vale la seguente disuguaglianza larga ${\textstyle \ 0\leq I\leq {\frac {X}{\alpha )).}$

Supponiamo inoltre che per la variabile aleatoria $X$ esiste $\mathbb {E} [X],$ allora:

P\left(X\geq \alpha \right)=\mathbb {E} [I].

Il valore atteso è definito come somma di tutti i valori che la variabile aleatoria può assumere moltiplicati per la probabilità che tale variabile assuma effettivamente tali valori: nel nostro caso

\mathbb {E} [I]=0\cdot P(I=0)+1\cdot P(I=1)=P(I=1).

Ma ancora, la probabilità che $I$ sia uguale a 1 è proprio la probabilità che $X$ sia maggiore o uguale ad $\alpha$

\mathbb {E} [I]\leq \mathbb {E} \left[{\frac {X}{\alpha ))\right].

Il valore atteso mantiene la disuguaglianza degli argomenti poiché si tratta di una funzione non decrescente, in vista del fatto che gli argomenti sono variabili non negative.

Basti pensare alla definizione di valore atteso, nel caso discreto e quello continuo, la quale genera serie a termini positivi in un caso, e integrali di funzioni positive nell’altro.

\mathbb {E} \left[{\frac {X}{\alpha ))\right]={\frac {\mathbb {E} [X]}{\alpha ))

Per la linearità del valore atteso.

Quindi si conclude che

P\left(X\geq \alpha \right)\leq {\frac {\mathbb {E} [X]}{\alpha )).

Disuguaglianza di Čebyšëv

Partendo dall’appena dimostrata disuguaglianza possiamo ottenere, come corollario, il seguente enunciato:

${\displaystyle P(|X-\mathbb {E} [X]|\geq \gamma )\leq {\frac {Var(X)}{\gamma ^{2))))$

con parametro $\gamma$ positivo.

Per farlo definiamo una variabile aleatoria $X:\Omega \rightarrow \mathbb {R}$ e associamo ad essa la variabile aleatoria

$Y=(X-\mathbb {E} [X])^{2}.$

Così definita $Y$ è una variabile aleatoria non negativa, pertanto applichiamo ad essa la disuguaglianza di Markov, ottenendo

{\displaystyle P\left(Y\geq \gamma ^{2}\right)\leq {\frac {\mathbb {E} [Y]}{\gamma ^{2))}\iff P\left((X-\mathbb {E} [X])^{2}\geq \gamma ^{2}\right)\leq {\frac {\mathbb {E} [(X-\mathbb {E} [X])^{2}]}{\gamma ^{2))))

a destra otteniamo la definizione di varianza

${\textstyle Var(X)=\mathbb {E} [(X-\mathbb {E} [X])^{2}],}$

e sapendo che in generale $\forall x,\mu ,\alpha$ vale quanto segue

$(x-\mu )^{2}\geq \alpha ^{2}\iff |x-\mu |\geq |\alpha |$

otteniamo quanto si voleva dimostrare, cioè

P(|X-\mathbb {E} [X]|\geq \gamma )\leq {\frac {Var(X)}{\gamma ^{2))},

che può anche essere riscritta ponendo il parametro ${\displaystyle t={\frac {\gamma }{\sqrt {Var(X)))))$

P(|X-\mathbb {E} [X]|\geq t{\sqrt {Var(X))))\leq {\frac {1}{t^{2))},

possiamo inoltre semplificare la scrittura usando, anziché la varianza, lo strumento statistico della deviazione standard, definito proprio come sua radice.

P(|X-\mathbb {E} [X]|\geq t\sigma )\leq {\frac {1}{t^{2))}.

Legge debole dei grandi numeri

La disuguaglianza di Čebyšëv, viene inoltre utilizzata nella famosa legge dei grandi numeri, di cui qui verrà dimostrata il suo enunciato cosiddetto “debole”.

L’enunciato è il seguente:

Consideriamo una popolazione di $N$ elementi di variabili aleatorie indipendenti tutte di valore atteso $\mu$ e varianza ${\displaystyle \sigma ^{2))$ .

\{X_{n}\}_{n\in \mathbb {N} ,\ n\leq N}\subset \mathbb {R}

\mathbb {E} [X_{n}]=\mu ,\ \forall n

Var(X_{n})=\sigma ^{2},\ \forall n.

E definendo lo stimatore del valor medio ${\displaystyle {\bar {X))_{N}={\frac {1}{N))\sum _{n=1}^{N}X_{n))$ si ha

\forall \epsilon \in \mathbb {R} ^{+}\lim _{N\rightarrow \infty }P(|{\bar {X))_{N}-\mu |<\epsilon )=1.

Il che vuol dire che aumentando la grandezza della popolazione in nostro possesso, lo stimatore del valor medio va sempre di più a coincidere con il valore atteso.

Dimostrazione

Applichiamo la disuguaglianza di Čebyšëv allo stimatore del valor medio:

{\displaystyle P(|{\bar {X))_{N}-\mathbb {E} [{\bar {X))_{N}]|\geq \epsilon )\leq {\frac {Var({\bar {X))_{N})}{\epsilon ^{2))))

per ogni $\epsilon \in \mathbb {R} ^{+}.$

Per le proprietà di linearità del valore atteso abbiamo che in generale la media aritmetica di variabili aleatorie di diverso valore atteso corrisponde a uno stimatore di valore atteso pari alla media aritmetica dei singoli valori attesi.

Nel nostro caso tutte le $X_{n}$ hanno lo stesso valore atteso $\mu$ , pertanto

\mathbb {E} [{\bar {X))_{N}]={\frac {1}{N))\sum _{n=1}^{N}\mathbb {E} [X_{n}]=\mu .

Poiché le $X_{n}$ sono indipendenti tra di loro vale quanto segue $\forall a,b\in \mathbb {R} ,\forall i,j\in \mathbb {N}$ tale che $i\leq j\leq N$

Var(aX_{i}+bX_{j})=a^{2}Var(X_{i})+b^{2}Var(X_{j}).

Nel nostro caso quindi abbiamo che

Var({\bar {X))_{N})={\frac {1}{N^{2))}\sum _{n=1}^{N}Var(X_{n})={\frac {\sigma ^{2)){N)).

Quindi riscriviamo la nostra relazione alla luce di quanto detto

P(|{\bar {X))_{N}-\mu |\geq \epsilon )\leq {\frac {\sigma ^{2)){N\epsilon ^{2))}\rightarrow 1-P(|{\bar {X))_{N}-\mu |\geq \epsilon )\geq 1-{\frac {\sigma ^{2)){N\epsilon ^{2))}.

Il primo termine può essere riscritto mediante il complementare dell’evento di cui stiamo calcolando la probabilità

1-P(|{\bar {X))_{N}-\mu |\geq \epsilon )=P(|{\bar {X))_{N}-\mu |<\epsilon ).

Ma comunque la probabilità di qualunque evento è al più 1:

1\geq P(|{\bar {X))_{N}-\mu |<\epsilon )\geq 1-{\frac {\sigma ^{2)){N\epsilon ^{2))}.

Pertanto se portiamo al limite tale espressione otteniamo quanto stavamo cercando per il teorema del confronto:

\lim _{N\rightarrow \infty }P(|{\bar {X))_{N}-\mu |<\epsilon )=1.

Il che vuol dire che è certo l’evento preso in considerazione, ovvero che definitivamente la distanza tra ${\displaystyle {\bar {X))_{N))$ e $\mu$ è maggiorata da $\epsilon$ arbitrario positivo

\forall \epsilon >0\ \exists {\bar {N))\ t.c.\forall N>{\bar {N))

|{\bar {X))_{N}-\mu |<\epsilon .

Il che significa in conclusione, per definizione di limite, che

\lim _{N\rightarrow \infty }{\bar {X))_{N}=\mu .

°°°°°

Disuguaglianza di Čebyšëv

La disuguaglianza di Čebyšëv è usata soprattutto nell’ambito della teoria probabilistica e più raramente nell’ambito di serie di dati reali.

Spesso la disuguaglianza di Čebyšëv viene indicata come disuguaglianza di Markov, di cui è un corollario.

La disuguaglianza venne pubblicata la prima volta nel 1853 da Irénée-Jules Bienaymé e riscoperta indipendentemente da Pafnutij L’vovič Čebyšëv alcuni anni dopo (pertanto viene anche citata come disuguaglianza di Bienaymé-Čebyšëv).

Descrizione

Nell’ambito delle variabili casuali (v.c.) essa afferma che se la v.c. $X$ ha valore atteso $\mu$ e la varianza $\sigma ^{2}$ e $\lambda$ è un numero reale positivo, allora la probabilità che $X$ assuma un valore compreso tra $\mu - \lambda \sigma$ e $\mu + \lambda \sigma$ è maggiore di ${\textstyle 1-1/\lambda ^{2))$ .

In altre parole afferma che, dato un carattere di cui sono noti solamente media aritmetica $\mu$ e deviazione standard $\sigma$ , possiamo conoscere la probabilità che una variabile casuale possa avere valori esterni a un intervallo simmetrico rispetto alla media aritmetica.

In altri termini questo teorema ci assicura che, indipendentemente dalla distribuzione della variabile casuale, la probabilità che questa assuma valori distanti dalla media più di $\lambda$ volte la deviazione standard è al massimo $1 / \lambda^2$

Otteniamo quindi il limite inferiore della probabilità di $\Pr \left(|X-\mu |\leq \lambda \cdot \sigma \right)$ espresso con la formula:

{\displaystyle \Pr \left(|X-\mu |\leq \lambda \cdot \sigma \right)\geq \ 1-{\frac {1}{\lambda ^{2))))

cioè:

\Pr(\mu -\lambda \sigma \leq X\leq \mu +\lambda \sigma )\geq \ 1-{\frac {1}{\lambda ^{2))}

da cui si può ottenere anche il limite superiore della probabilità di $\Pr \left(|{X-\mu }|\geq \lambda \cdot \sigma \right)$ espresso come:

1-\Pr \left(|{X-\mu }|\leq \lambda \cdot \sigma \right)\leq \ {\frac {1}{\lambda ^{2))}

che equivale a scrivere:

{\displaystyle \Pr \left(|{X-\mu }|\geq \lambda \cdot \sigma \right)\leq \ {\frac {1}{\lambda ^{2))))

cioè:

{\displaystyle \Pr(X\leq \mu -\lambda \sigma \ \cup \ X\geq \mu +\lambda \sigma )\leq {\frac {1}{\lambda ^{2))))

Nell’ambito della statistica descrittiva essa afferma che l’intervallo di valori compreso tra $\mu - \lambda \sigma$ e $\mu + \lambda \sigma$ ha un livello di confidenza di almeno $(1-1/\lambda ^{2})$ .

Fisz dimostrò che per le variabili dotate di media e varianza non è possibile trovare una disuguaglianza migliore di quella di Čebyšëv, a meno che non si impongano dei vincoli alla distribuzione della variabile.

Da questa disuguaglianza si deduce che

almeno il 75% dei valori sono compresi tra $\mu - 2 \sigma$ e $\mu + 2 \sigma$
almeno l’89% dei valori sono compresi tra $\mu - 3 \sigma$ e $\mu + 3 \sigma$
almeno il 94% dei valori sono compresi tra $\mu - 4 \sigma$ e $\mu + 4 \sigma$
almeno il 96% dei valori sono compresi tra $\mu - 5 \sigma$ e $\mu + 5 \sigma$
almeno il 99% dei valori sono compresi tra $\mu - 10 \sigma$ e $\mu + 10 \sigma$

indipendentemente da come sono distribuiti i valori.

Dimostrazione probabilistica

Per ogni evento $A$ , sia $I_A$ la variabile casuale indicatore di $A$ , cioè $I_A$ è uguale a $1$ se l’evento $A$ accade e $0$ altrimenti. Allora si ha:

\Pr(|X-\mu |\geq \lambda \sigma )=\operatorname {E}(I_((|X-\mu |\geq \lambda \sigma )))=\operatorname {E}(I_(((X-\mu )^{2}\geq (\lambda \sigma )^{2))})=\Pr((X-\mu )^{2}\geq (\lambda \sigma )^{2})

Dalla disuguaglianza di Markov segue poi:

\Pr((X-\mu )^{2}\geq (\lambda \sigma )^{2})\leq {\frac {\operatorname {E}((X-\mu )^{2})}{(\lambda \sigma )^{2))}

Si ha quindi:

\Pr(|X-\mu |\geq \lambda \sigma )\leq {\frac {1}{\lambda ^{2))}{\frac {\operatorname {E}((X-\mu )^{2})}{\sigma ^{2))}={\frac {1}{\lambda ^{2))}

°°°°°

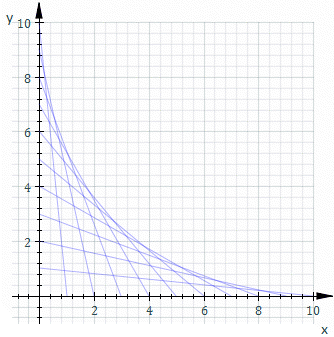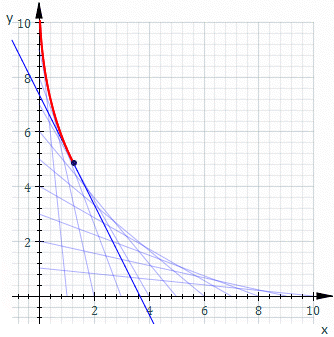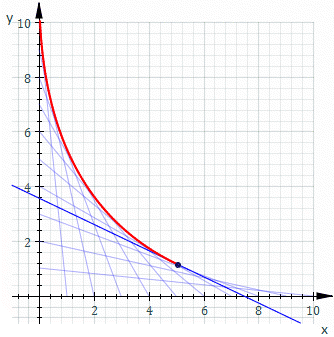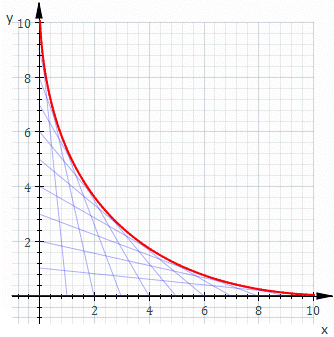
Inviluppo (matematica)

In matematica,

l’inviluppo di una famiglia o di un insieme di curve piane è la curva tangente a ciascun membro della famiglia in almeno un punto.

La più semplice espressione analitica di un inviluppo di curve nel piano $(x,y)$ è data dalla coppia di equazioni

F(x,y,t)=0\qquad \qquad (1)

{\frac {\partial F(x,y,t)}{\partial t))=0\qquad \qquad (2)

dove la famiglia è implicitamente definita da (1); la (2), in termini informali, individua i punti in cui

la F(x, y, t) rimane “costante”.

Ovviamente deve essere possibile fare la derivata parziale rispetto a t di ciascuna curva della famiglia.

Per una famiglia di curve nel piano definite dalle equazioni parametriche $(x(t,p),y(t,p))$ , l’inviluppo si ottiene dall’equazione

{\partial x \over \partial t}{\partial y \over \partial p}={\partial y \over \partial t}{\partial x \over \partial p}

dove al variare del parametro p si ottengono le differenti curve della famiglia.

Esempio

Animazione che mostra l'inviluppo di una famiglia di rette a inclinazione negativa

Animazione che mostra l’inviluppo di una famiglia di rette a inclinazione negativa

Si consideri il piano cartesiano, I quadrante, e in esso le rette passanti per i punti (0, k – t) e (t, 0), dove k è una costante e la famiglia di rette è generata dal variare del parametro t.

La generica equazione di tali rette è y = −(k − t)x/t + k − t, ovvero, in forma implicita:

F(x,y,t)=t^{2}+t(y-x-k)+kx=0

Uguagliando a zero la derivata rispetto a t si ha:

{\frac {\partial F(x,y,t)}{\partial t))=2t+y-x-k=0

da cui:

t={\frac {-y+x+k}{2))

Sostituendo t nella definizione di F(x, y, t) si ottiene:

x^{2}-2xy+y^{2}-2kx-2ky+k^{2}=0

che è l’equazione della curva di inviluppo.

°°°°°

Lascia un commento

Pubblicato da salvatore di lucia su 13 aprile 2021 in MATEMATICA

Tag: Semicontinuità

Lascia un commento Cancella risposta

WebMaster : Salvatore Di Lucia

iMathematica :
più La si visita più Vi aiuta a risolvere ... iProblemi ...!
Statistiche del Sito:
- 1.043.687 visite
Ricerca Articolo
Cerca
Calendario
aprile: 2021

L M M G V S D

1 2 3 4

5 6 7 8 9 10 11

12 13 14 15 16 17 18

19 20 21 22 23 24 25

26 27 28 29 30

« Mar Mag »
Traduttore
I Grandi Matematici
Questo slideshow richiede JavaScript.
Visitatori del Sito :

Free counters
Grandi Matematici
Questo slideshow richiede JavaScript.
Categorie
Categorie
Articoli Mese
Articoli Mese
Giugno 2024

– Analisi Matematica I

— Grafici di funzioni

—Derivate

Maggio 2024

– Analisi Matematica I

— Grafici di funzioni

—Limiti
Aprile 2024

– Analisi Matematica I

— Numeri Reali

—Funzioni
Marzo 2024

– Analisi Matematica I

— Teoria degli Insiemi

—Relazioni Matematiche
Febbraio 2024

– Logica Matematica

— Tavole Verità

—Tautologie
Gennaio 2024

– Logica Matematica

— Proposizione logica

— Connettivi Logici
Dicembre 2023

– Algebra I

— Funzione di Eulero

— Teorema di Eulero
Novembre 2023

– Algebra I

— Divisibilità Partizioni

— Congruenze in
Ottobre 2023

– Analisi I

— Successioni di numeri reali

— Esercitazioni
Settembre 2023

– Analisi I

— Funzioni

— Segno di Funzione
Agosto 2023

– Algebra

— Equazioni

— Disequazioni
Luglio 2023

– Algebra

— Strutture Algebriche
Giugno 2023

– Calcolo Combinatorio

— Coefficiente Binomiale
Maggio 2023

– Funzioni Polinomiali

— Scomposizione di Polinomi
Aprile 2023

– Funzioni Reale di variabile Reale

— Studio di Funzione
Marzo 2023

– Funzioni Reale di variabile Reale

— Studio di Funzione
Febbraio 2023

– Insieme dei Numeri Complessi

— ℂ
Gennaio 2023

– Insiemi Numerici

— ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ=ℚ ∪ 𝕀
Dicembre 2022

– Algebra Lineare

— Sistemi Lineari

—Esercitazione
Novembre 2022

– Algebra Lineare

— Matrice, Determinante

—Esercitazione
Ottobre 2022

– Analisi I

— Integrali

—Esercitazione
Settembre 2022

– Analisi I

— Derivata

—Esercitazione
Agosto 2022

– Analisi I

— Teoremi sui Limiti

—Esercitazione
Luglio 2022

– Analisi I

— Teoria dei Limiti

—Esercitazione
Giugno 2022

– Analisi II

— Equazioni Differenziali

—Esercitazione
Maggio 2022

– Analisi II

— Equazioni Differenziali

—Esercitazione
Aprile 2022

– Analisi II

— Equazioni Differenziali
Marzo 2022

– Analisi II

— Equazioni Differenziali
Febbraio 2022

– Analisi I

— Integrali
Gennaio 2022

– Analisi I

— Derivate
Dicembre 2021

– Algebra

— Polinomi
Novembre 2021

– Corso di Analisi II

— Topologia Generale
Ottobre 2021

– Corso di Analisi II

— Equazioni Differenziali
Settembre 2021

– Corso di Analisi

— Coniche

— Quadriche
Agosto 2021

– Corso di Analisi

— Classificazione delle Funzioni
Luglio 2021

– Corso di Analisi

— Successioni Numeriche
Giugno 2021

– Corso di Analisi

— Serie Numeriche
Maggio 2021

– Corso di Analisi

— Serie Numeriche
Aprile 2021

– Corso di Analisi

—Tipi di Funzioni
Marzo 2021

– Corso di Analisi

—Tipi di Funzioni
Febbraio 2021

– Corso di Analisi

—Confronto tra Funzioni
Gennaio 2021

– Corso di Analisi

—Confronto tra Funzioni
Dicembre 2020

– Corso di Analisi

—Limiti Teoremi
Novembre 2020

– Corso di Analisi

—Limiti
Ottobre 2020

– Corso di Analisi

—o-piccolo

_O-grande

_Esercizi sui Limiti
Settembre 2020

– Corso di Analisi

—Punto di accumulazione

—Simboli di Landau
Agosto 2020

– Corso di Analisi

—Classe di resto modulo n

__Equazioni Congruenziali
Luglio 2020

– Corso di Analisi

—Classe di resto modulo n

__Equazioni Congruenziali
Giugno 2020

– Corso di Analisi

—Classe di resto modulo n

__Equazioni Congruenziali
Maggio 2020

– Corso di Analisi

—Classe di resto modulo n

__Equazioni Congruenziali
Aprile 2020

– Corso di Analisi

—Classe di resto modulo n

__Equazioni Congruenziali
Marzo 2020

– Corso di Analisi

—Le Coniche
Febbraio 2020

– Corso di Analisi

—Le Coniche
Gennaio 2020

– Corso di Analisi

—Le Coniche
Dicembre 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia e Esercizi
Novembre 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia e Esercizi
Ottobre 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia e Esercizi
Settembre 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia e Esercizi
Agosto 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia e Esercizi
Luglio 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia
Giugno 2019

– Corso di Analisi

—Istituzione di Analisi Superiore

—Topologia
Maggio 2019

– Corso di Analisi

—Istituzione di Analisi Superiore
Aprile 2019

– Corso di Analisi

—Istituzione di Analisi Superiore
Marzo 2019

– Corso di Analisi

—Istituzione di Analisi Superiore
Febbraio 2019

– Corso di Analisi

—Istituzione di Analisi Superiore
Gennaio 2019

– Corso di Analisi

—Istituzione di Analisi Superiore
Gennaio 2018

– Corso di Analisi

—Teoria degli Insiemi
Dicembre 2018

– Corso di Analisi

—Istituzione di Analisi Superiore
Novembre 2018

– Corso di Analisi

—Istituzione di Analisi Superiore
Ottobre 2018

– Corso di Analisi

—Istituzione di Analisi Superiore
Settembre 2018

– Corso di Analisi

—Istituzione di Analisi Superiore
Agosto 2018

– Corso di Analisi

—Esercizi sui Numeri Complessi
Luglio 2018

– Corso di Analisi

—Esercizi sui Numeri Complessi
Giugno 2018

– Corso di Analisi

—Insieme dei Numeri Complessi
Maggio 2018

– Corso di Analisi

—Teoria dei Numeri
Aprile 2018

– Corso di Analisi

—Teoria degli Insiemi
Marzo 2018

– Corso di Analisi

—Teoria degli Insiemi
Febbraio 2018

– Corso di Analisi

—Teoria degli Insiemi
Dicembre 2017

– Corso di Analisi I
—Manuale di iMathematica
Novembre 2017

– Corso di Analisi I
—Manuale di iMathematica
Ottobre 2017

– Corso di Analisi I
—Manuale di iMathematica
Settembre 2017

– Corso di Analisi I
—Manuale di iMathematica
Agosto 2017

– Corso di Analisi I
—Manuale di iMathematica
Luglio 2017

– Corso di Analisi I
—Manuale di iMathematica
Giugno 2017

– Corso di Analisi I
—Manuale di iMathematica
Maggio 2017

- Corso di Analisi
--Trasformazioni Lineari
Aprile 2017

- Corso di Analisi
--Equazioni Differenziali Lineari
Marzo 2017

- Corso di Analisi
--Equazioni Differenziali Ordinarie
Febbraio 2017

- Corso di Analisi
--Precorso
Gennaio2017

- Corso di Analisi
--Serie Trigonometriche
Dicembre 2016

- Corso di Analisi
--Strutture Fondamentali dell'Analisi
Novembre 2016

- Corso di Analisi
--Strutture Fondamentali dell'Analisi
Ottobre 2016

- Corso di Analisi
--Strutture Fondamentali dell'Analisi
Settembre 2016

- Corso di Analisi
-- Integrali Impropri
Agosto 2016

- Corso di Analisi
-- Funzioni Analitiche
Luglio 2016

- Corso di Analisi
-- Integrale Curvilineo
Giugno 2016

- Corso di Analisi
-- Integrale definito
Maggio 2016

- Corso di Analisi
-- Integrale di Riemann
Aprile 2016

- Corso di Analisi
-- Derivate di ordine superiore
Marzo 2016

- Corso di Analisi
-- Derivate
Febbraio 2016

- Corso di Analisi
-- Esercizi sulle Serie
Gennaio 2016

- Corso di Analisi
-- Serie
Dicembre 2015

– Corso di Analisi
— Successioni di funzioni
Novembre 2015

- Corso di Analisi
-- Funzioni Continue
Ottobre 2015

- Corso di Analisi
--Teoria dei Limiti
Settembre 2015

- Corso di Analisi
-- Spazi Metrici
Agosto 2015

- Corso di Analisi
-- Numeri Complessi
Luglio 2015

- Corso di Analisi
-- Numeri Reali
Giugno 2015

- Integrali Impropri
Maggio 2015

- Funzioni Analitiche II
Aprile 2015

- Funzioni Analitiche I
Marzo 2015

- Integrale Teoria Generale II
Febbraio 2015

- Integrale Teoria Generale I
Gennaio 2015

- Derivate di ordine superiore
Dicembre 2014

- Derivata teoria generale.
Novembre 2014

- Serie teoria generale.-
Ottobre 2014

- Limiti teoria generale II
Settembre 2014

- Limiti teoria generale I
Agosto 2014

- Spazi Metrici.
Luglio 2014

– Funzioni Reali II
Giugno 2014

- Funzioni Reali I
Maggio 2014

- Disequazioni Trascendenti -
Aprile 2014

– Disequazioni
Marzo 2014

- Fascio di Coniche II
Febbraio 2014

- Fascio di Coniche I
Gennaio 2014

– Geometria Analitica I
Dicembre 2013

– Trigonometria
Novembre 2013

– Metodo di Tartenville
Ottobre 2013

- Dimostrazione Formale
Settembre 2013

– Logica Matematica
Agosto 2013

– Insiemi
Luglio 2013

- Logica
Giugno 2013

- Analisi Matematica II
Maggio 2013

– Metrica Euclidea
Aprile 2013

– Derivazione
Marzo 2013

– Elementi di Topologia
Febbraio 2013

- Le Serie
Gennaio 2013

– Teoria degli Insiemi
Dicembre 2012

– Teoria degli Insiemi
Novembre 2012

– Teoria degli Insiemi
Ottobre 2012

– Teoria degli Insiemi
Settembre 2012

– Teoria degli Insiemi
Agosto 2012

– Teoria degli Insiemi
Luglio 2012

– Teoria degli Insiemi
Giugno 2012

– Teoria degli Insiemi
Maggio 2012

– Teoria degli Insiemi
Aprile 2012

– Teoria degli Insiemi
Marzo 2012

– Teoria degli Insiemi
Febbraio 2012

– Teoria degli Insiemi
Gennaio 2012

– Teoria degli Insiemi
Dicembre 2011

– Teoria degli Insiemi
Novembre 2011

– Teoria degli Insiemi
Ottobre 2011

– Teoria degli Insiemi
Settembre 2011

– Teoria degli Insiemi
Agosto 2011

– Teoria degli Insiemi
Luglio 2011

– Teoria degli Insiemi
Giugno 2011

– Teoria degli Insiemi
Maggio 2011

– Teoria degli Insiemi
Aprile 2011

– Teoria degli Insiemi
Marzo 2011

– Teoria degli Insiemi
Febbraio 2011

– Teoria degli Insiemi
Gennaio 2011

– Teoria degli Insiemi
Dicembre 2010

– Teoria degli Insiemi
Tag
Applicazioni del piano complesso in se stesso Condizione Sufficiente coordinate polari Criteri di convergenza per serie a termini non negativi Criterio di Cauchy Definizione di derivata DERIVATE DI ORDINE SUPERIORE Differenziale dominio di una funzione equazione differenziale Equazione di Laplace Equazioni e Disequazioni Trascendenti formula di Taylor funzione arcocosecante funzione arcocoseno funzione arcosecante funzione arcoseno funzione armonica funzione biunivoca Funzione concava Funzione convessa funzione esponenziale Funzione Iniettiva Funzione inversa funzione periodica Funzione ricorsiva funzione suriettiva Funzione Trigonometriche funzioni discontinue funzioni trigonometriche grafico di una funzione gruppo identità di Eulero Il Pensiero Matematico Insieme aperto Insieme chiuso Integrale di Lebesgue integrale di riemann Integrali curvilinei di funzioni complesse Integrali impropri contenenti un parametro integrazione per parti isometria Le Coniche Limite (+) infinito per x che tende a un valore (+) infinito limite di una funzione Limite di una Serie numerica con Excel Limiti Limiti calcolo mediante limiti notevoli matrici Numeri Complessi Numeri Reali Permutazione Polinomi polinomi a coefficienti reali Polinomio di Taylor Problema di Cauchy prodotto scalare prodotto vettoriale Punti singolari isolati punto di accumulazione punto isolato Radice ennesima di x∈R x≧0 regole di derivazione Schema generale di applicazione dell'integrale Serie Armonica Serie di Taylor simmetria assiale Spazio Metrico Completo teorema di Cauchy teorema di Lagrange teorema di Rolle trasformazioni lineari trigonometria vettori vettori linearmente dipendenti
Instagram
Amministrazione
- Registrati
- Accedi
- Flusso di pubblicazione
- Feed dei commenti
- WordPress.com
e-mail

Inserisci il tuo indirizzo e-mail per iscriverti a questo blog e ricevere notifiche di nuovi messaggi per e-mail.

Indirizzo email:

Unisciti a 235 altri iscritti
Vivi l’Attimo!
Articoli e Pagine
- Densità di ℚ in ℝ
- Cambio di variabile per gli integrali doppi : Lezione 20
- FUNZIONE ARMONICA
- Formula di Taylor con resto di Peano
- La serie armonica generalizzata
- Teorema dei valori intermedi
- Limite infinito per x tendente a un valore finito
- teorema dei moltiplicatori di Lagrange in tre variabili : Lezione 16
- Metodo di Lagrange.
- Funzione Calcolabile
Autore
Social
- Visualizza il profilo di sdlrmr@gmail.com su Facebook
- Visualizza il profilo di rmr4448 su Twitter
- Visualizza il profilo di rmr4448 su Instagram
- Visualizza il profilo di salvatore-di-lucia-a52302b8 su LinkedIn
- Google+