Salvatore Di Lucia
Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)
Derivata di una funzione in un punto e derivata come funzione
Studiamo un argomento di fondamentale importanza in Analisi Matematica:
la definizione di derivata, o derivata prima di una funzione.
Qui introduciamo la definizione di derivata e la spieghiamo per filo e per segno, con svariati esempi:
vediamo
1.) cos’è la derivata di una funzione in un punto
e
2.) cos’è la derivata prima intesa come funzione.
Prima di procedere, un piccolo riepilogo.
Ricordiamo che nella precedente lezione abbiamo definito
il rapporto incrementale di una funzione y = f(x) in un punto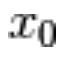 
con incremento h
come:
Indice
-
Derivata in un punto
-
Esempi
-
-
Derivata come funzione
-
Calcolo
-
1.) Derivata di una funzione in un punto
La derivata di una funzione y = f(x) in un punto 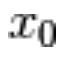del suo dominio
è
il limite del rapporto incrementale al tendere dell’incremento h a zero.
Ci sono diversi modi per denotare la derivata di una funzione in un punto:
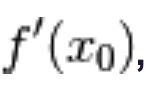oppure 
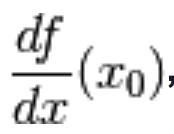o ancora 
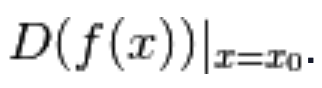Tutti questi simboli si riconducono alla medesima definizione, che possiamo tradurre nella seguente formula:
Tutto qui? In effetti no, possiamo dare altre due definizioni.
Chiamiamo
2.) derivata sinistra nel punto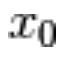
il limite del rapporto incrementale calcolato da sinistra:
Diciamo
3.) derivata destra nel punto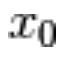
il limite del rapporto incrementale calcolato da destra:
Vi anticipiamo che se si considera
un generico punto x e si calcola la derivata punto per punto,
la derivata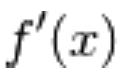 
si può intendere come una funzione “correlata” con f(x).
Ma andiamo con ordine…
Esempi
sulla derivata di una funzione in un punto
1.) Consideriamo la funzione f(x) = 4x e calcoliamone la derivata in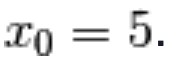 
.
Prima di tutto ci serve il rapporto incrementale nel punto:
Effettuiamo le valutazioni sostituendo i rispettivi argomenti al posto di x nell’espressione della funzione:
Il rapporto incrementale appena calcolato non dipende da h,
dunque passare al limite per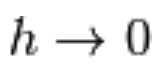 
è ininfluente.
In definitiva
la derivata della funzione f(x) nel punto 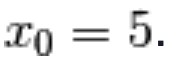è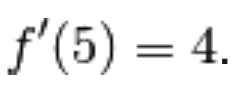 
.
°°°°°
2.) Prendiamo la funzione logaritmica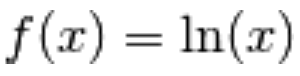 
e calcoliamone la derivata nel punto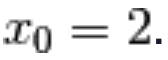 
.
Il punto 2 appartiene al dominio della funzione Dom(f)=(0, +∞) e sappiamo che, prima di tutto, va calcolato
il rapporto incrementale nel punto,
con incremento h generico:
Ora, seguendo la definizione di derivata in un punto, passiamo al limite per h tendente a zero:
Grazie a una proprietà dei logaritmi, secondo cui
il logaritmo di un rapporto è uguale alla differenza dei logaritmi,
riscriviamo il limite nella forma:
Osserviamo che per 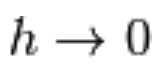risulta che 
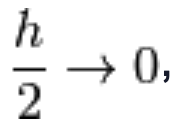quindi possiamo usare il limite notevole dei logaritmi:
Per poterlo usare moltiplichiamo e dividiamo a denominatore per 2, di modo che risulti:
Si conclude che
la derivata di y = ln(x) nel punto 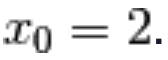è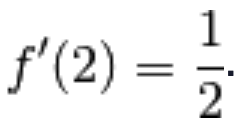 
°°°°°
Derivata prima di una funzione
Abbiamo definito la derivata di una funzione in un punto, e lo ripetiamo:
se la derivata di una funzione in un punto esiste,
è un valore reale, ossia un numero.
Ora è il momento di estendere la definizione alla totalità dei punti in cui è possibile calcolare la derivata, e dunque di parlare di
derivata prima di una funzione (intesa come funzione).
In realtà, a questo punto,
dovremmo preoccuparci delle condizioni che garantiscono l’esistenza della derivata in un punto,
ma lo faremo in una lezione a parte (funzione derivabile).
Dunque:
se abbiamo una funzione y = f(x) con dominio Dom(f),
supponiamo che
la derivata puntuale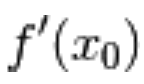 
esista in ogni punto 
del dominio.
Consideriamo
la funzione che associa a ogni punto x del dominio di f la corrispondente derivata nel punto: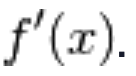 
Chiamiamo questa funzione
derivata prima della funzione f,
e la indichiamo con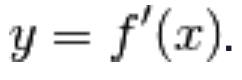 
È molto importante non fare confusione:
-
la derivata di una funzione in un punto, se esiste, è un numero;
-
la derivata prima di una funzione, o la derivata di una funzione, è una funzione.
In sintesi,
se si specifica in un punto abbiamo a che fare con un valore;
se si parla solo di derivata, ci riferiamo ad una funzione.
Come calcolare la derivata prima
Per calcolare la derivata prima di una funzione usiamo
la definizione di derivata di una funzione in un punto , considerando però come un punto generico, ossia come variabile.
Esempio
Calcoliamo la derivata prima della funzione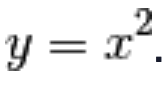 
Dalla definizione di derivata prima in un punto ,
considerando generico, calcoliamo prima il rapporto incrementale:
Facciamo i conti e sviluppiamo il quadrato del binomio:
Ora che abbiamo l’espressione analitica del rapporto incrementale,
passiamo al limite per h tendente a zero
e otteniamo:
Ricordando che denota un generico punto e trattandolo alla stregua di una variabile, ne deduciamo che
la derivata della funzione 
In una delle successive lezioni studieremo
il significato geometrico della derivata
e, successivamente, spiegheremo qual è
il suo significato analitico:
essa esprime
la ripidità con cui la funzione cresce o descresce nell’intorno del punto.
Vedremo che il calcolo della derivata di una funzione non è così meccanico come sembra, e che non richiede di passare dalla definizione come limite del rapporto incrementale.
Prima però ci occupiamo della condizione di derivabilità di una funzione,
ossia
la condizione di esistenza della derivata in un punto.
°°°°°
Link Lezione precedente
Esercitazione
Soluzione:
°°°°°
Soluzione:
°°°°°
Soluzione:
°°°°°
Soluzione:
°°°°°
Soluzione:
°°°°°
Soluzione:
°°°°°
Soluzione:
°°°°°
Soluzione:
°°°°°
Soluzione:
°°°°°
Soluzione:
iMathematica 
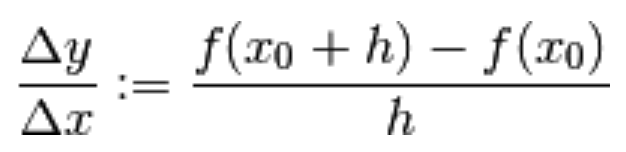
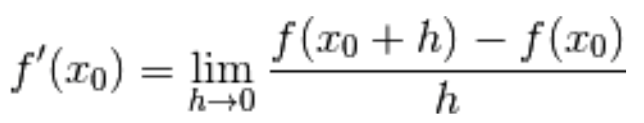
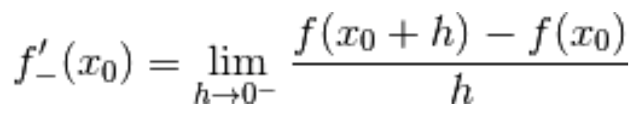
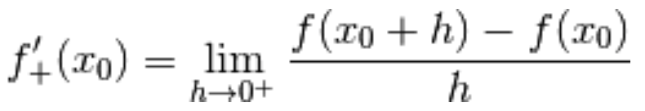
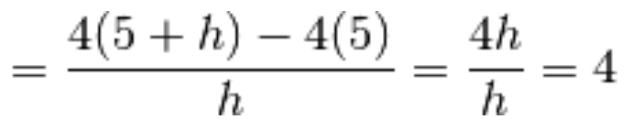
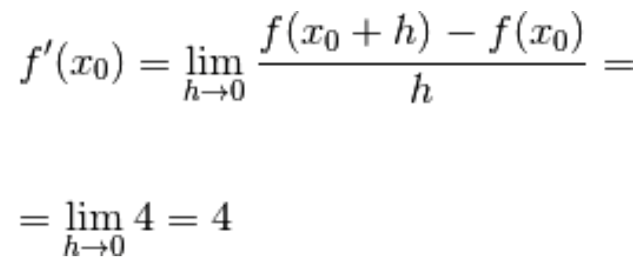
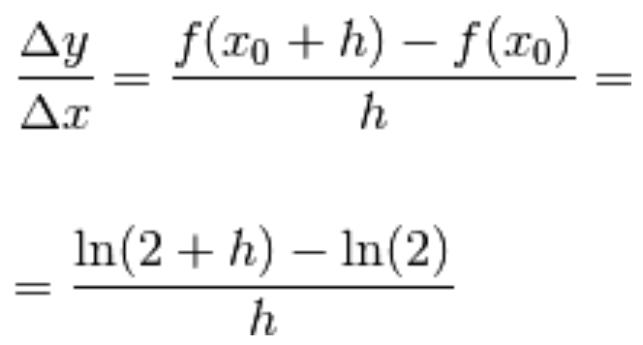
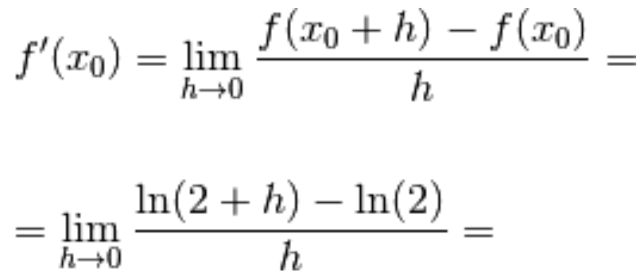
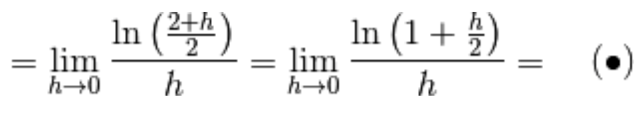
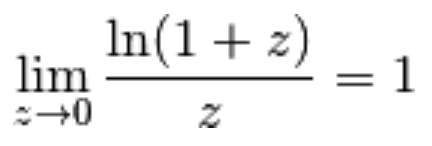
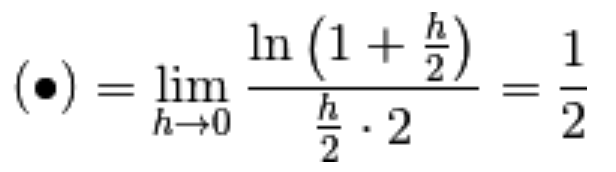
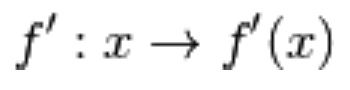
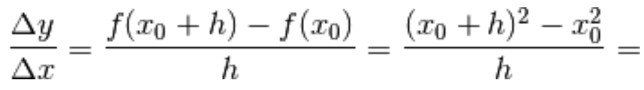
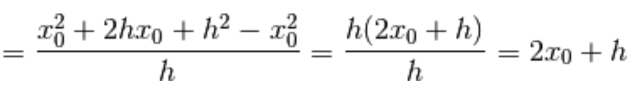
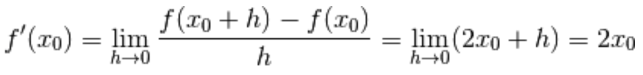
Devi effettuare l'accesso per postare un commento.