Passaggio al limite sotto segno di integrale






Passaggio al limite sotto segno di integrale
In analisi matematica,
per passaggio al limite sotto segno di integrale si intende la possibilità di calcolare il limite di una successione di integrali come l’integrale del limite della successione delle funzioni integrande:
-

Tale tipo di operazione si presenta in un gran numero di applicazioni, e l’assenza di teoremi con ipotesi sufficientemente generali che permettano lo scambio del passaggio al limite con l’operazione di integrazione è uno dei motivi che hanno portato alla definizione dell’integrale di Lebesgue in sostituzione dell’integrale di Riemann.
i teoremi di passaggio al limite sotto il segno di integrale sono lo strumento principale per stabilire se, per una data successione di funzioni,
implica la convergenza in norma L1.
°°°°°
Integrale di Riemann
Nell’integrale di Riemann, la possibilità di passare al limite sotto integrale è strettamente legata alla convergenza uniforme:
il teorema principale in questo contesto afferma che lo scambio è possibile se l’insieme di integrazione è limitato e la convergenza è uniforme.
La dimostrazione di questo teorema segue quasi immediatamente dalle definizioni,
in quanto
-
![{\displaystyle 0\leq \left|\int _{E}[f_{k}(x)-f(x)]\mathrm {d} x\right|\leq \int _{E}|f_{k}(x)-f(x)|\mathrm {d} x\leq |E|\sup {\{f_{k}(x)-f(x)\))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6781cb37c4b226231d69a6ebbeb24aae33d529c7)
che tende a 0 per la convergenza uniforme.
Né un’ipotesi né l’altra sono sufficienti a garantire lo scambio:
per un insieme non limitato si può prendere ad esempio la successione
-
![{\displaystyle f_{n}(x)={\frac {1}{n))\chi _{[n,2n]}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd89e92dae7e6bd64232034191f8cd77ab95c86d)
mentre
in un insieme limitato un semplice esempio è
-
![{\displaystyle f_{n}(x)=n\chi _{\left[0,{\frac {1}{n))\right]}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6f9f3e47b0ab47c7eca988910c62d5d9359a486)
In entrambi i casi,
le funzioni tendono puntualmente alla funzione identicamente nulla
(la prima in  ,
,
la seconda in [0,1]),
che ha ovviamente integrale 0,
ma ogni membro della successione ha integrale 1.
Le generalizzazioni di questo teorema mantengono comunque almeno in parte l’ipotesi di convergenza uniforme:
si può dimostrare che
se la successione {fn} tende puntualmente ad una funzione f in un insieme E,
converge uniformemente in ogni compatto contenuto in E ed esiste una funzione g ad integrale finito tale che
-

per ogni x e per ogni n, allora lo scambio è possibile.
Un ulteriore problema è la possibilità che, pur esistendo il limite puntuale di una successione di funzioni integrabili secondo Riemann, questo non sia a sua volta integrabile:
ad esempio,
-

si ha una successione di funzioni integrabili (con integrale nullo) che converge puntualmente alla funzione di Dirichlet, che non è integrabile secondo Riemann.
Anche in questo caso l’eventuale presenza della convergenza uniforme permette di affermare l’integrabilità della funzione limite.
°°°°°
Integrale di Lebesgue
Nell’integrale di Lebesgue i teoremi di passaggio al limite sotto integrali hanno ipotesi considerevolmente più deboli rispetto a quelli relativi all’integrale di Riemann.
I due teoremi principe sono
e
Il primo afferma che lo scambio tra le operazioni di limite e di integrazione è possibile se le funzioni sono non negative
e
se la successione è monotona crescente,
ovvero se:
-

per ogni x e per ogni n,
mentre
il secondo si applica nel caso di funzioni dominate da una funzione integrabile,
ovvero in cui esiste una funzione g, ad integrale finito,
tale che:
-

per ogni x e per ogni n.
Le funzioni utilizzate devono essere misurabili per dare un senso alla successione di integrali, e non è necessario richiedere come ipotesi che la funzione limite sia misurabile poiché il limite di una successione di funzioni misurabili è misurabile.
I teoremi possono essere leggermente ampliati richiedendo che le ipotesi
(la convergenza e, rispettivamente, la monotonia e l’essere dominate)
siano verificate in tutto l’insieme d’integrazione ad eccezione di un insieme di misura nulla.
Un ulteriore indebolimento del teorema della convergenza monotona si ha rilassando l’ipotesi di non negatività, in quanto è sufficiente che una di esse abbia integrale maggiore di  affinché, per la monotonia, condivida questa proprietà con tutte quelle seguenti.
affinché, per la monotonia, condivida questa proprietà con tutte quelle seguenti.
Il teorema si può applicare anche a successioni decrescenti di funzioni,
ma in tal caso si deve chiedere che uno degli integrali sia minore di  .
.
Un terzo importante risultato,
dimostrato a partire dal teorema della convergenza monotona e usato nella dimostrazione della convergenza dominata, è
-

In una forma equivalente, ma più inconsueta, si ha:
-

Un corollario immediato del teorema della convergenza dominata, usato talvolta in teoria della probabilità,
afferma che lo scambio è possibile se l’insieme d’integrazione è limitato e le funzioni sono uniformemente limitate
(cioè esiste una costante M tale che |fn| < M per ogni n e per quasi ogni x).
Il risultato ha tuttavia un suo valore autonomo, in quanto le sue ipotesi possono essere raffinate sostituendo la convergenza quasi ovunque con la convergenza in misura.
°°°°°
Applicazioni
Serie
Un caso particolare di successione di funzioni sono le somme parziali di una serie,
ovvero le successioni del tipo
-

I teoremi di passaggio al limite si trasferiscono immediatamente a questo caso:
sfruttando la linearità dell’integrale nel caso di somme finite,
si ottiene che la formula
-

è valida nel caso di addendi positivi (convergenza monotona) o nel caso in cui le somme parziali siano limitate da una funzione integrabile (convergenza dominata), e in particolare nel caso di convergenza assoluta.
In alcuni casi è possibile in questo modo capire se la somma di una serie di funzioni è finita o meno calcolando la somma dei suoi integrali; un esempio è la somma
-

dove {qn) è una numerazione dei razionali; integrando per serie
(grazie al teorema della convergenza monotona)
e poiché l’integrale di ogni addendo è minore di A / 2n per una costante A, l’integrale di f risulta finito, e quindi f stessa continua quasi ovunque.
Un caso molto particolare è dato nel caso in cui la misura considerata sia la misura del conteggio:
in tal caso gli integrali si riducono semplicemente alle somme, e nelle ipotesi dei teoremi di scambio
(non negatività e convergenza assoluta)
si ottiene la formula
-

Dominio variabile
In alcuni casi a variare non è la funzione, ma il dominio d’integrazione; ovvero, data una successione decrescente {En} di insiemi, ci si chiede se
-

In tal caso, ci si può ricondurre al caso moltiplicando per la funzione indicatrice di En, ovvero ponendo
-

Si ottiene così una successione di funzioni ai quali possono essere applicati i teoremi precedenti.
Scambio di integrali
Lo stesso argomento in dettaglio: Teorema di Fubini.
Il calcolo effettivo della quasi totalità degli integrali multipli dipende in maniera cruciale dalla possibilità di ridurre l’integrale in più dimensioni a più integrali in una dimensione, ovvero di poter avere:[4]
-

dove per semplicità si è scritto un integrale sui reali in due dimensioni.
La possibilità di effettuare questo scambio dipende in maniera critica dai teoremi di passaggio al limite:
nella dimostrazione del teorema di Tonelli, che afferma la possibilità dello scambio per funzioni positive, vi è infatti la possibilità di approssimare ogni funzione misurabile con una successione crescente di funzioni semplici alla quale poter applicare il teorema della convergenza monotona.
Teoria della probabilità
La teoria della probabilità, che si basa sulla teoria della misura, ha tra i suoi strumenti anche i teoremi di passaggio al limite sotto segno di integrale:
due tra gli usi di questo sono nella prova dell’esistenza
e
del teorema dell’optional stopping per supermartingale.
Nella prima, dopo aver espresso una variabile casuale integrabile X (cioè in L1) come limite di una successione crescente {Xn} di funzioni in L2
(per cui si può dimostrare più facilmente l’esistenza della media condizionata),
si può usare la convergenza monotona per ottenere la media condizionata  come limite di
come limite di  ; nel secondo invece la convergenza dominata è usata per stabilire sotto quali condizioni
; nel secondo invece la convergenza dominata è usata per stabilire sotto quali condizioni
(equilibrando quelle richieste sulla successione {Xn} e quelle sul tempo d’arresto τ)
si ha
-

in modo da poter usare le proprietà delle supermartingale per ottenere
-

e in particolare, per martingale,
-

risultato che è spesso utile nel calcolo di  .
.
°°°°°



Segue Esercitazione

Teorema della convergenza monotona
teorema della convergenza monotona si identificano diversi teoremi relativi alla convergenza di successioni o serie.
Successioni di numeri reali
Nel caso di successioni di numeri,
il teorema della convergenza monotona afferma che se  è una successione monotona di numeri reali,
è una successione monotona di numeri reali,
allora la successione converge se e solo se è limitata.
La dimostrazione del fatto che se una successione monotona converge allora essa è limitata, viene dal fatto che ogni successione convergente è limitata.
°°°°°
Convergenza
la convergenza è la proprietà di una certa funzione o successione di possedere un limite finito di qualche tipo, al tendere della variabile (o dell’indice eventualmente) verso certi valori in un punto o all’infinito.
Il concetto si applica dunque a vari campi della matematica, tutti in qualche modo collegati ma con interpretazioni leggermente diverse.
Limite di una funzione
Data una funzione continua  , si dice che
, si dice che  converge (o tende) al limite finito
converge (o tende) al limite finito  per
per  che tende ad
che tende ad 
se per ogni  esiste un
esiste un  tale che per ogni
tale che per ogni  che soddisfa
che soddisfa  si ha che
si ha che  . Ovvero:
. Ovvero:
-

Analogamente,
si dice che  converge al limite finito
converge al limite finito  per
per  che tende a infinito se per ogni
che tende a infinito se per ogni  esiste un
esiste un  tale che per ogni
tale che per ogni  soddisfacente la condizione
soddisfacente la condizione  si ha che
si ha che  . Ovvero:
. Ovvero:
-

Convergenza di una successione in una dimensione
La convergenza di una successione numerica  di numeri reali si verifica quando per
di numeri reali si verifica quando per  , a partire da un certo indice in poi tutti i termini della successione si trovino nell’intorno di un punto, detto limite della successione.
, a partire da un certo indice in poi tutti i termini della successione si trovino nell’intorno di un punto, detto limite della successione.
Matematicamente questo si esprime dicendo che una successione  converge al numero a per
converge al numero a per  , e si scrive
, e si scrive  , se
, se  esiste un indice naturale
esiste un indice naturale  , in generale dipendente da
, in generale dipendente da  , tale che la
, tale che la
 per ogni
per ogni  .
.
Questo garantisce che tutti i termini della successione, caratterizzati da  , siano contenuti nell’intorno
, siano contenuti nell’intorno

Una successione convergente è necessariamente limitata.
Convergenza delle serie
Si consideri una successione di elementi  .
.
Si definisce serie associata ad  la somma:
la somma:
-

Per ogni indice  della successione,
della successione,
si definisce serie delle somme parziali  associata a
associata a 
la somma dei termini della successione  da
da  a
a  :
:
-

Si dice che la serie  è convergente al limite
è convergente al limite  se la relativa successione delle somme parziali
se la relativa successione delle somme parziali  converge a
converge a  .
.
Ovvero,
si verifica che:
-

se e solo se:
-

Il limite sopra enunciato si dice somma della serie, ed esprime il carattere della serie.
Teorema della convergenza
Formalmente il concetto di convergenza di una successione è simile a quello delle funzioni  .
.
Data una successione di numeri reali  che converge a un certo limite
che converge a un certo limite  per
per  , si ha:
, si ha:
-

In modo equivalente,
per ogni  esiste un intorno
esiste un intorno  , in generale dipendente da
, in generale dipendente da  , tale che:
, tale che:
-

qualora si verifichi:
-

Questo garantisce che, come i termini della successione sono contenuti nell’intorno di  , allo stesso modo tutti i valori della funzione sono contenuti nell’intorno:
, allo stesso modo tutti i valori della funzione sono contenuti nell’intorno:
-

Ogni funzione convergente è quindi necessariamente limitata, e questo implica anche il concetto di continuità di una funzione.
Enunciato
Si supponga di avere una funzione  tale che
tale che  con α appartenente a un certo intervallo
con α appartenente a un certo intervallo  .
.
Si può porre:
-

Si ha dunque:
-

Se esiste  tale che:
tale che:
-
![{\displaystyle [\alpha -\delta ,\alpha +\delta ]=J\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/129b4b36cfd2d8b0a9cd37572daaf2659007870a)
e se esiste  tale che:
tale che:
-

allora si ha:
-
Se  allora:
allora:
-

Dimostrazione
Premesso che:
-

si ha:
-

Oltre ad avere:
-

si verifica che:
-

Si ottiene:
-

Poiché  tende a zero quando i tende a infinito,
tende a zero quando i tende a infinito,
la successione converge.
Si ponga per assurdo che nell’intervallo vi sia β, radice della funzione diversa da α.
Si ha:
-

Il fatto che:
-

è assurdo,
e quindi α è l’unica radice dell’intervallo.
Convergenza delle successioni e serie di funzioni
Per le successioni  vi sono le seguenti tipologie di convergenza:
vi sono le seguenti tipologie di convergenza:
-

-

Per le serie di funzioni  vi sono le seguenti tipologie di convergenza:
vi sono le seguenti tipologie di convergenza:
-
La convergenza puntuale si verifica se la serie numerica  converge per ogni
converge per ogni  .
.
-
La convergenza uniforme si verifica se la successione delle somme parziali converge uniformemente.
-
La convergenza totale si verifica se esiste una serie numerica  convergente tale che:
convergente tale che:
-

-
per ogni  e
e  .
.
Convergenza di variabili casuali
Data una successione di variabili casuali  , vi sono più tipi di convergenza:
, vi sono più tipi di convergenza:
-
La convergenza in distribuzione:
-

-
dove  e
e  sono le funzioni di ripartizione delle
sono le funzioni di ripartizione delle  e del limite
e del limite  rispettivamente.
rispettivamente.
-
La convergenza in probabilità:
-

-
La convergenza quasi certa:
-

-
La convergenza in media r-esima:
-

°°°°°
L’implicazione inversa,
cioè che se una successione monotona è limitata allora essa converge, si dimostra nel modo seguente:
prendiamo una successione monotona crescente (nel caso di successioni decrescenti la dimostrazione è analoga) e chiamiamo  .
.
La limitatezza fa sì che esista finito un elemento
-

tale che per ogni elemento della successione vale  .
.
Scelto un  arbitrario, esiste un indice
arbitrario, esiste un indice  tale che
tale che
-

perché  non è maggiorante di
non è maggiorante di  .
.
Se quindi scegliamo un indice  , la monotonia della successione implica
, la monotonia della successione implica  e quindi vale
e quindi vale
-

Dall’arbitrarietà di  segue la convergenza di
segue la convergenza di  a
a  .
.
Serie di numeri
Nel caso di serie di numeri,
il teorema della convergenza monotona afferma che se per ogni coppia di numeri naturali j e k il numero  è reale e non negativo e
è reale e non negativo e  ,
,
allora:
-

°°°°°
Successioni di funzioni
Nel caso di successioni di funzioni,
il teorema della convergenza monotona, anche detto teorema di Beppo Levi, afferma che
e
-

-

allora
 è misurabile in
è misurabile in  e:
e:
-

dove l’integrale è di Lebesgue.
Si noti che il valore di ogni integrale può essere infinito.
Dimostrazione
Sia  una successione non decrescente di funzioni misurabili non negative e si ponga:
una successione non decrescente di funzioni misurabili non negative e si ponga:
-

Per la proprietà di monotonìa dell’integrale, è immediato vedere che:
-

Si vuole provare la diseguaglianza nell’altra direzione, cioè:
-

Dalla definizione di integrale segue che esiste una successione non decrescente  di funzioni semplici non negative che convergono puntualmente a
di funzioni semplici non negative che convergono puntualmente a  quasi ovunque e tali che:
quasi ovunque e tali che:
-

Perciò basta provare che per ogni  si ha:
si ha:
-

Si vuole provare che se  è una funzione semplice e:
è una funzione semplice e:
-

quasi ovunque, allora:
-

Spezzando la funzione  nelle sue parti a valori costanti,
nelle sue parti a valori costanti,
questo si riduce al caso in cui  è la funzione indicatrice di un insieme.
è la funzione indicatrice di un insieme.
Il risultato che si vuole provare è il seguente.
Si supponga che  sia un insieme misurabile
sia un insieme misurabile
e
 sia una successione non descrescente di funzioni misurabili su
sia una successione non descrescente di funzioni misurabili su  tali che:
tali che:
-

per quasi tutti gli  .
.
Allora:
-

Per provare questo risultato si fissi ε > 0 e si definisca la successione di insiemi misurabili:
-

Per la monotonìa dell’integrale, segue che per ogni  si ha:
si ha:
-

Per ipotesi:
-

a meno di un insieme di misura 0.
Quindi per l’addittività numerabile di  :
:
-

Poiché questo è vero per ogni ε positivo, segue la tesi.
°°°°°
Teorema della convergenza dominata
il teorema della convergenza dominata fornisce una condizione sufficiente sotto la quale
Enunciato
e
tale che esiste il limite:
-

Se esiste una funzione  tale che
tale che
-

nel qual caso  si dice dominata da
si dice dominata da  ,
,
allora si ha:
-

-

ovvero
 in tutto
in tutto 
Dimostrazione
Dal momento che
 denota il limite quasi ovunque della successione
denota il limite quasi ovunque della successione  ,
,
allora
la successione è misurabile e dominata da  , e quindi integrabile.
, e quindi integrabile.
Si vuole mostrare che:
-
 per qualunque S contenuto in X.
per qualunque S contenuto in X.
Dal momento che:
-

e che:
-
 per ogni x
per ogni x
allora si può usare il lemma di Fatou inverso e si ha:
-

Ma dal momento che:
-

allora:
-

e il fatto che sia vero per ogni S ci consente di affermare che:
-

dimostrando la tesi.
°°°°°
Esercitazione

Calcolare

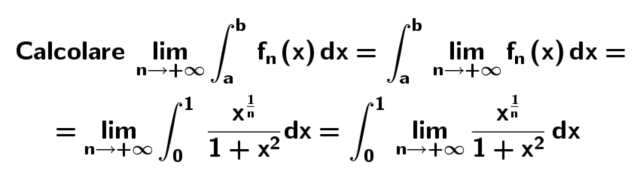
Soluzione:
 ∀x∈[0,1]
∀x∈[0,1]
1.) Un Primo passo: Convergenza puntuale della funzione
2.) Secondo passo: Cerchiamo una funzione g(x) integrabile ovvero 
Grafico:

°°°°°

Calcolare:
Soluzione:
Grafico:
°°°°°

Calcolare:
Soluzione:
Grafico:
°°°°°

Calcolare:
Soluzione:
Grafico:
°°°°°

Calcolare:
Soluzione:
Grafico:
°°°°°

Calcolare:
Soluzione:
Grafico:
°°°°°

Calcolare:
Soluzione:
Grafico:
°°°°°

Calcolare:
Soluzione:
Grafico:
°°°°°
Tag: Passaggio al limite sotto segno di integrale


![]()
![]()

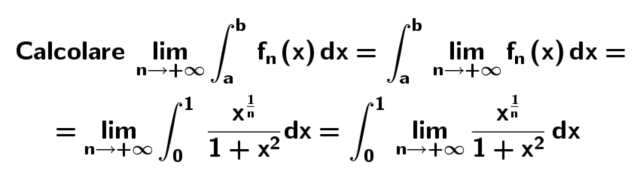
 ∀x∈[0,1]
∀x∈[0,1]


![]()
![]()
![]()
![]()
![]()
![]()
![]()





![{\displaystyle 0\leq \left|\int _{E}[f_{k}(x)-f(x)]\mathrm {d} x\right|\leq \int _{E}|f_{k}(x)-f(x)|\mathrm {d} x\leq |E|\sup {\{f_{k}(x)-f(x)\))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6781cb37c4b226231d69a6ebbeb24aae33d529c7)
![{\displaystyle f_{n}(x)={\frac {1}{n))\chi _{[n,2n]}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd89e92dae7e6bd64232034191f8cd77ab95c86d)

![{\displaystyle f_{n}(x)=n\chi _{\left[0,{\frac {1}{n))\right]}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6f9f3e47b0ab47c7eca988910c62d5d9359a486)




































































![{\displaystyle [\alpha -\delta ,\alpha +\delta ]=J\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/129b4b36cfd2d8b0a9cd37572daaf2659007870a)















































































Devi effettuare l'accesso per postare un commento.