Salvatore Di Lucia
Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)
Funzione derivabile e condizione di derivabilità
Nelle verifiche delle Scuole Superiori (seconda prova di Matematica inclusa) e negli esami universitari spesso ci si imbatte in esercizi che richiedono di studiare la derivabilità di una funzione in un punto o su un insieme.
Per risolverli è essenziale conoscere la definizione di funzione derivabile, e comprendere a fondo il significato algebrico e analitico della condizione di derivabilità in un punto o su un intervallo.
Nelle lezioni precedenti abbiamo studiato
la definizione di derivata di una funzione y = f(x) in un punto,
e abbiamo anche visto che cos’è
la derivata di una funzione intesa come funzione.
Qui ci occupiamo della
condizione di derivabilità di una funzione in un punto,
o meglio
la condizione necessaria e sufficiente che garantisce l’esistenza della derivata di una funzione in un punto 
del suo dominio.
Indice
-
Condizione
-
Esempio: funzione derivabile
-
Esempio: funzione non derivabile
-
Attenzione!
-
-
Teoremi utili
-
Approfondimenti
Condizione di derivabilità e funzione derivabile
Dalla definizione sappiamo che
la derivata di una funzione y = f(x) in un punto 
è definita
come
il limite del rapporto incrementale della funzione nel punto:
Molto semplicemente,
la condizione di derivabilità in un punto sussiste
quando il suddetto limite esiste.
Cosa significa, in concreto?
Dobbiamo fare riferimento alla definizione di limite:
un limite esiste finito
se i due limiti sinistro e destro esistono finiti
e hanno lo stesso valore.
Mettiamo tutto assieme e formalizziamo ciò che abbiamo scritto.
Definizione di funzione derivabile in un punto
Una funzione è derivabile in un punto
se esiste la derivata prima nel punto considerato,
ossia
se il limite sinistro e il limite destro del rapporto incrementale calcolato nel punto esistono finiti e uguali.
In simboli, y = f(x) è una funzione derivabile in un punto
se:
Funzione derivabile da sinistra, funzione derivabile da destra
Vi ricordate
la definizioni di derivata sinistra e la definizioni di derivata destra che abbiamo dato nella lezione sulla definizione di derivata?
Esse ci permettono di riscrivere la condizione di derivabilità in modo equivalente: possiamo dire che
una funzione è derivabile in un punto
se la derivata sinistra e la derivata destra esistono finite
e coincidono nel punto.
Più in generale possiamo dire che:
se la derivata sinistra 
esiste finita,
allora
f è una funzione derivabile da sinistra in ;
se la derivata destra 
esiste finita,
allora
f è una funzione derivabile da destra in .
affinché
una funzione f sia derivabile in un punto
è necessario e sufficiente che essa sia
ivi derivabile sia da sinistra che da destra (valori finiti)
e che la derivata sinistra e la derivata destra coincidano.
Anche se queste definizioni aggiuntive possono sembrare inutili, si rivelano molto utili nella pratica.
Un esempio?
Se abbiamo una funzione che ha il dominio con estremi finiti,
come f : [a, b]→R,
non ha senso parlare di derivabilità di f nel punto 
,
ma solo di derivabilità da destra;
non ha senso parlare di derivabilità di f nel punto 
ma solo di derivabilità da sinistra.
In una delle successive lezioni ci occuperemo del
rapporto che sussiste tra
la condizione di derivabilità
e
la continuità di una funzione.
Ora vediamo due esempi:
1.) uno con funzione derivabile in un punto,
2.) uno con una funzione che non è derivabile in un punto.
Esempio 1:
funzione derivabile in un punto
Consideriamo la funzione 
e il punto 
.
Tale funzione è derivabile nel punto considerato, infatti
Poiché
i due limiti sinistro e destro del rapporto incrementale calcolato nel punto esistono finiti
e
hanno lo stesso valore,
la funzione è effettivamente derivabile nel punto.
Esempio 2:
funzione non derivabile in un punto
Consideriamo la funzione 
e il punto .
Tale funzione non è derivabile nel punto,
infatti:
A titolo di cronaca,
in una delle lezioni successive classificheremo
i punti di non derivabilità che si possono presentare nel caso delle funzioni reali di variabile reale.
Attenzione alla verifica della condizione di derivabilità
È importante ribadire, in questa sede, un aspetto che spesso viene frainteso e che ha pesanti conseguenze nella risoluzione degli esercizi.
Per stabilire se
una funzione è derivabile in un punto
dobbiamo confrontare
il limite sinistro e il limite destro del rapporto incrementale
e non della derivata prima.
Lo sottolineiamo perché molti studenti tendono a studiare
i limiti sinistro e destro della derivata prima.
Questo metodo in generale non funziona e, tranne che in particolarissimi casi, non corrisponde alla definizione di derivabilità in un punto
(ne parliamo in dettaglio qui:
studiare la derivabilità di una funzione:
metodo delle derivate?
Poiché
il metodo del rapporto incrementale è quello che si basa direttamente sulla definizione di funzione derivabile,
è quello che dovremo usare negli esercizi.
Teoremi utili sulla derivabilità di una funzione
Prima di concludere vi proponiamo alcuni teoremi che inizialmente potranno sembrarvi astratti, ma che si rivelano utili nella risoluzione degli esercizi.
Questi teoremi verranno usati in modo implicito un’infinità di volte,
sia a livello teorico che pratico, ed è bene metterli in chiaro da subito.
Enunciamoli prima in termini generali e poi in modo più rigoroso.
1.) La somma (differenza) di due funzioni derivabili è derivabile.
Date f e g,
sia 
un punto in cui entrambe le funzioni sono derivabili.
Allora
la funzione somma f+g (differenza f-g) è derivabile in 
.
2.) Il prodotto di due funzioni derivabili è derivabile.
Date f e g,
sia un punto in cui entrambe le funzioni sono derivabili.
Allora
la funzione prodotto f · g è derivabile in .
3.) Il quoziente di due funzioni derivabili è derivabile.
Date f e g,
sia un punto in cui entrambe le funzioni sono derivabili e tale che 
.
Allora
la funzione rapporto 
è derivabile in .
4.) La composizione di funzioni derivabili è derivabile.
Date f e f,
sia 
un punto in cui f è derivabile
e
supponiamo che g sia derivabile in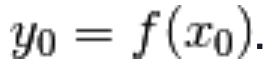 
.
Allora
la funzione composta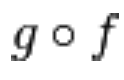 
è derivabile in .
Riguardo alle dimostrazioni, seguiranno in automatico quando dimostreremo
le regole per il calcolo delle derivate (1-3)
e
il teorema di derivazione della funzione composta (4).
Sappiate che questi quattro teoremi,
insieme a ciò che studieremo nella lezione sui punti di non derivabilità,
vi permetteranno di risolvere
qualsiasi esercizio relativo allo studio della derivabilità delle funzioni.
°°°°°
Link Lezione precedente
Esercitazione
Soluzione:
Grafico:
°°°°°
Soluzione:
Grafico :
°°°°°
Soluzione:
Grafico :
°°°°°
Soluzione:
Grafico :
°°°°°
Soluzione:
Grafico :
°°°°°
Soluzione:
Grafico :
°°°°°
Soluzione:
Grafico :
°°°°°
Soluzione:
Grafico :
°°°°°
Soluzione:
Grafico :
°°°°°
Soluzione:
Grafico :
°°°°°
Soluzione:
Grafico :
°°°°°
Soluzione:
Grafico :
°°°°°
Soluzione:
iMathematica 
Devi effettuare l'accesso per postare un commento.