Georg Friedrich Bernard Riemann
WebMaster : Salvatore Di Lucia
iMathematica :
più La si visita più Vi aiuta a risolvere ... iProblemi ...!Statistiche del Sito:
- 1.043.687 visite
Ricerca Articolo
Calendario
Traduttore
I Grandi Matematici
Questo slideshow richiede JavaScript.
Visitatori del Sito :
Grandi Matematici
Questo slideshow richiede JavaScript.
Categorie
Articoli Mese
-
Giugno 2024
– Analisi Matematica I
— Grafici di funzioni
—Derivate
Maggio 2024
– Analisi Matematica I
— Grafici di funzioni
—Limiti
Aprile 2024
– Analisi Matematica I
— Numeri Reali
—Funzioni
Marzo 2024
– Analisi Matematica I
— Teoria degli Insiemi
—Relazioni Matematiche
Febbraio 2024
– Logica Matematica
— Tavole Verità
—Tautologie
Gennaio 2024
– Logica Matematica
— Proposizione logica
— Connettivi Logici
Dicembre 2023
– Algebra I
— Funzione di Eulero
— Teorema di Eulero
Novembre 2023
– Algebra I
— Divisibilità Partizioni
— Congruenze in
Ottobre 2023
– Analisi I
— Successioni di numeri reali
— Esercitazioni
Settembre 2023
– Analisi I
— Funzioni
— Segno di Funzione
Agosto 2023
– Algebra
— Equazioni
— Disequazioni
Luglio 2023
– Algebra
— Strutture Algebriche
Giugno 2023
– Calcolo Combinatorio
— Coefficiente Binomiale
Maggio 2023
– Funzioni Polinomiali
— Scomposizione di Polinomi
Aprile 2023
– Funzioni Reale di variabile Reale
— Studio di Funzione
Marzo 2023
– Funzioni Reale di variabile Reale
— Studio di Funzione
Febbraio 2023
– Insieme dei Numeri Complessi
— ℂ
Gennaio 2023
– Insiemi Numerici
— ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ=ℚ ∪ 𝕀
Dicembre 2022
– Algebra Lineare
— Sistemi Lineari
—Esercitazione
Novembre 2022
– Algebra Lineare
— Matrice, Determinante
—Esercitazione
Ottobre 2022
– Analisi I
— Integrali
—Esercitazione
Settembre 2022
– Analisi I
— Derivata
—Esercitazione
Agosto 2022
– Analisi I
— Teoremi sui Limiti
—Esercitazione
Luglio 2022
– Analisi I
— Teoria dei Limiti
—Esercitazione
Giugno 2022
– Analisi II
— Equazioni Differenziali
—Esercitazione
Maggio 2022
– Analisi II
— Equazioni Differenziali
—Esercitazione
Aprile 2022
– Analisi II
— Equazioni Differenziali
Marzo 2022
– Analisi II
— Equazioni Differenziali
Febbraio 2022
– Analisi I
— Integrali
Gennaio 2022
– Analisi I
— Derivate
Dicembre 2021
– Algebra
— Polinomi
-
Novembre 2021
– Corso di Analisi II
— Topologia Generale
Ottobre 2021
– Corso di Analisi II
— Equazioni Differenziali
Settembre 2021
– Corso di Analisi
— Coniche
— Quadriche
Agosto 2021
– Corso di Analisi
— Classificazione delle Funzioni
Luglio 2021
– Corso di Analisi
— Successioni Numeriche
Giugno 2021
– Corso di Analisi
— Serie Numeriche
Maggio 2021
– Corso di Analisi
— Serie Numeriche
Aprile 2021
– Corso di Analisi
—Tipi di Funzioni
Marzo 2021
– Corso di Analisi
—Tipi di Funzioni
Febbraio 2021
– Corso di Analisi
—Confronto tra Funzioni
Gennaio 2021
– Corso di Analisi
—Confronto tra Funzioni
Dicembre 2020
– Corso di Analisi
—Limiti Teoremi
Novembre 2020
– Corso di Analisi
—Limiti
Ottobre 2020
– Corso di Analisi
—o-piccolo
_O-grande
_Esercizi sui Limiti
Settembre 2020
– Corso di Analisi
—Punto di accumulazione
—Simboli di Landau
Agosto 2020
– Corso di Analisi
—Classe di resto modulo n
__Equazioni Congruenziali
Luglio 2020
– Corso di Analisi
—Classe di resto modulo n
__Equazioni Congruenziali
Giugno 2020
– Corso di Analisi
—Classe di resto modulo n
__Equazioni Congruenziali
Maggio 2020
– Corso di Analisi
—Classe di resto modulo n
__Equazioni Congruenziali
Aprile 2020
– Corso di Analisi
—Classe di resto modulo n
__Equazioni Congruenziali
Marzo 2020
– Corso di Analisi
—Le Coniche
Febbraio 2020
– Corso di Analisi
—Le Coniche
Gennaio 2020
– Corso di Analisi
—Le Coniche
Dicembre 2019
– Corso di Analisi
—Istituzione di Analisi Superiore
—Topologia e Esercizi
Novembre 2019
– Corso di Analisi
—Istituzione di Analisi Superiore
—Topologia e Esercizi
Ottobre 2019
– Corso di Analisi
—Istituzione di Analisi Superiore
—Topologia e Esercizi
Settembre 2019
– Corso di Analisi
—Istituzione di Analisi Superiore
—Topologia e Esercizi
Agosto 2019
– Corso di Analisi
—Istituzione di Analisi Superiore
—Topologia e Esercizi
Luglio 2019
– Corso di Analisi
—Istituzione di Analisi Superiore
—Topologia
Giugno 2019
– Corso di Analisi
—Istituzione di Analisi Superiore
—Topologia
Maggio 2019
– Corso di Analisi
—Istituzione di Analisi Superiore
Aprile 2019
– Corso di Analisi
—Istituzione di Analisi Superiore
Marzo 2019
– Corso di Analisi
—Istituzione di Analisi Superiore
Febbraio 2019
– Corso di Analisi
—Istituzione di Analisi Superiore
Gennaio 2019
– Corso di Analisi
—Istituzione di Analisi Superiore
Gennaio 2018
– Corso di Analisi
—Teoria degli Insiemi
Dicembre 2018
– Corso di Analisi
—Istituzione di Analisi Superiore
Novembre 2018
– Corso di Analisi
—Istituzione di Analisi Superiore
Ottobre 2018
– Corso di Analisi
—Istituzione di Analisi Superiore
Settembre 2018
– Corso di Analisi
—Istituzione di Analisi Superiore
Agosto 2018
– Corso di Analisi
—Esercizi sui Numeri Complessi
Luglio 2018
– Corso di Analisi
—Esercizi sui Numeri Complessi
Giugno 2018
– Corso di Analisi
—Insieme dei Numeri Complessi
Maggio 2018
– Corso di Analisi
—Teoria dei Numeri
Aprile 2018
– Corso di Analisi
—Teoria degli Insiemi
Marzo 2018
– Corso di Analisi
—Teoria degli Insiemi
Febbraio 2018
– Corso di Analisi
—Teoria degli Insiemi
Dicembre 2017
– Corso di Analisi I
—Manuale di iMathematicaNovembre 2017
– Corso di Analisi I
—Manuale di iMathematicaOttobre 2017
– Corso di Analisi I
—Manuale di iMathematicaSettembre 2017
– Corso di Analisi I
—Manuale di iMathematicaAgosto 2017
– Corso di Analisi I
—Manuale di iMathematicaLuglio 2017
– Corso di Analisi I
—Manuale di iMathematicaGiugno 2017
– Corso di Analisi I
—Manuale di iMathematicaMaggio 2017
- Corso di Analisi
--Trasformazioni LineariAprile 2017
- Corso di Analisi
--Equazioni Differenziali LineariMarzo 2017
- Corso di Analisi
--Equazioni Differenziali OrdinarieFebbraio 2017
- Corso di Analisi
--PrecorsoGennaio2017
- Corso di Analisi
--Serie TrigonometricheDicembre 2016
- Corso di Analisi
--Strutture Fondamentali dell'AnalisiNovembre 2016
- Corso di Analisi
--Strutture Fondamentali dell'AnalisiOttobre 2016
- Corso di Analisi
--Strutture Fondamentali dell'AnalisiSettembre 2016
- Corso di Analisi
-- Integrali ImpropriAgosto 2016
- Corso di Analisi
-- Funzioni AnaliticheLuglio 2016
- Corso di Analisi
-- Integrale CurvilineoGiugno 2016
- Corso di Analisi
-- Integrale definitoMaggio 2016
- Corso di Analisi
-- Integrale di RiemannAprile 2016
- Corso di Analisi
-- Derivate di ordine superioreMarzo 2016
- Corso di Analisi
-- DerivateFebbraio 2016
- Corso di Analisi
-- Esercizi sulle SerieGennaio 2016
- Corso di Analisi
-- SerieDicembre 2015
– Corso di Analisi
— Successioni di funzioniNovembre 2015
- Corso di Analisi
-- Funzioni ContinueOttobre 2015
- Corso di Analisi
--Teoria dei LimitiSettembre 2015
- Corso di Analisi
-- Spazi MetriciAgosto 2015
- Corso di Analisi
-- Numeri ComplessiLuglio 2015
- Corso di Analisi
-- Numeri RealiGiugno 2015
- Integrali Impropri
Maggio 2015
- Funzioni Analitiche II
Aprile 2015
- Funzioni Analitiche I
Marzo 2015
- Integrale Teoria Generale II
Febbraio 2015
- Integrale Teoria Generale I
Gennaio 2015
- Derivate di ordine superiore
Dicembre 2014
- Derivata teoria generale.
Novembre 2014
- Serie teoria generale.-
Ottobre 2014
- Limiti teoria generale II
Settembre 2014
- Limiti teoria generale IAgosto 2014
- Spazi Metrici.
Luglio 2014
– Funzioni Reali II
Giugno 2014
- Funzioni Reali I
Maggio 2014
- Disequazioni Trascendenti -
Aprile 2014
– Disequazioni
Marzo 2014
- Fascio di Coniche II
Febbraio 2014
- Fascio di Coniche I
Gennaio 2014
– Geometria Analitica I
Dicembre 2013
– Trigonometria
Novembre 2013
– Metodo di Tartenville
Ottobre 2013
- Dimostrazione Formale
Settembre 2013
– Logica Matematica
Agosto 2013
– Insiemi
Luglio 2013
- Logica
Giugno 2013
- Analisi Matematica II
Maggio 2013
– Metrica Euclidea
Aprile 2013
– Derivazione
Marzo 2013
– Elementi di Topologia
Febbraio 2013
- Le Serie
Gennaio 2013
– Teoria degli Insiemi
Dicembre 2012
– Teoria degli Insiemi
Novembre 2012
– Teoria degli Insiemi
Ottobre 2012
– Teoria degli Insiemi
Settembre 2012
– Teoria degli Insiemi
Agosto 2012
– Teoria degli Insiemi
Luglio 2012
– Teoria degli Insiemi
Giugno 2012
– Teoria degli Insiemi
Maggio 2012
– Teoria degli Insiemi
Aprile 2012
– Teoria degli Insiemi
Marzo 2012
– Teoria degli Insiemi
Febbraio 2012
– Teoria degli Insiemi
Gennaio 2012
– Teoria degli Insiemi
Dicembre 2011
– Teoria degli Insiemi
Novembre 2011
– Teoria degli Insiemi
Ottobre 2011
– Teoria degli Insiemi
Settembre 2011
– Teoria degli Insiemi
Agosto 2011
– Teoria degli Insiemi
Luglio 2011
– Teoria degli Insiemi
Giugno 2011
– Teoria degli Insiemi
Maggio 2011
– Teoria degli Insiemi
Aprile 2011
– Teoria degli Insiemi
Marzo 2011
– Teoria degli Insiemi
Febbraio 2011
– Teoria degli Insiemi
Gennaio 2011
– Teoria degli Insiemi
Dicembre 2010
– Teoria degli Insiemi
Tag
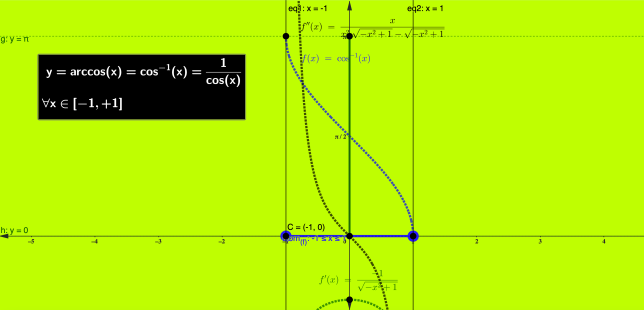
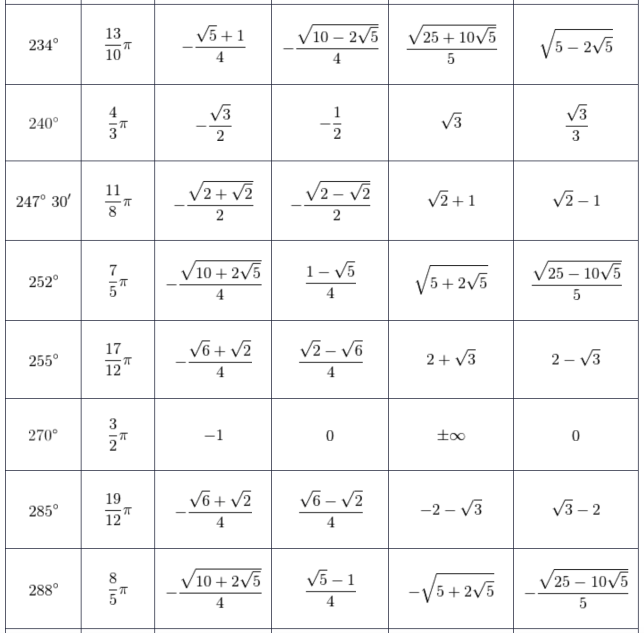
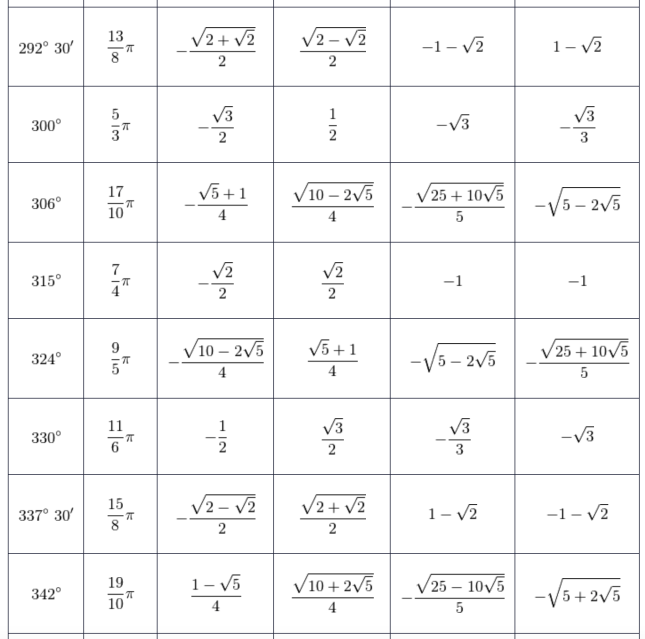
Applicazioni del piano complesso in se stesso Condizione Sufficiente coordinate polari Criteri di convergenza per serie a termini non negativi Criterio di Cauchy Definizione di derivata DERIVATE DI ORDINE SUPERIORE Differenziale dominio di una funzione equazione differenziale Equazione di Laplace Equazioni e Disequazioni Trascendenti formula di Taylor funzione arcocosecante funzione arcocoseno funzione arcosecante funzione arcoseno funzione armonica funzione biunivoca Funzione concava Funzione convessa funzione esponenziale Funzione Iniettiva Funzione inversa funzione periodica Funzione ricorsiva funzione suriettiva Funzione Trigonometriche funzioni discontinue funzioni trigonometriche grafico di una funzione gruppo identità di Eulero Il Pensiero Matematico Insieme aperto Insieme chiuso Integrale di Lebesgue integrale di riemann Integrali curvilinei di funzioni complesse Integrali impropri contenenti un parametro integrazione per parti isometria Le Coniche Limite (+) infinito per x che tende a un valore (+) infinito limite di una funzione Limite di una Serie numerica con Excel Limiti Limiti calcolo mediante limiti notevoli matrici Numeri Complessi Numeri Reali Permutazione Polinomi polinomi a coefficienti reali Polinomio di Taylor Problema di Cauchy prodotto scalare prodotto vettoriale Punti singolari isolati punto di accumulazione punto isolato Radice ennesima di x∈R x≧0 regole di derivazione Schema generale di applicazione dell'integrale Serie Armonica Serie di Taylor simmetria assiale Spazio Metrico Completo teorema di Cauchy teorema di Lagrange teorema di Rolle trasformazioni lineari trigonometria vettori vettori linearmente dipendentiInstagram
Amministrazione
-
Unisciti a 235 altri iscritti
Vivi l’Attimo!

Articoli e Pagine
Autore
Social









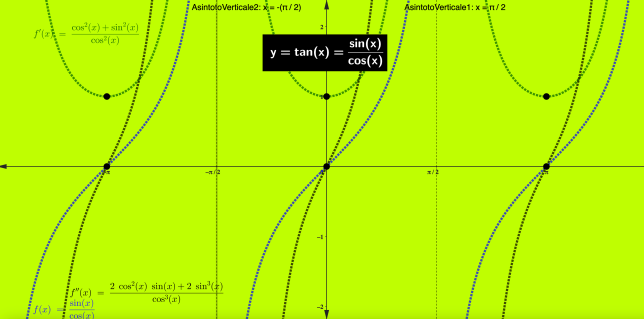
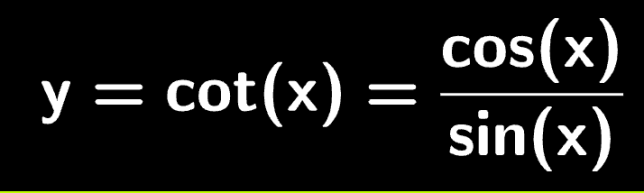



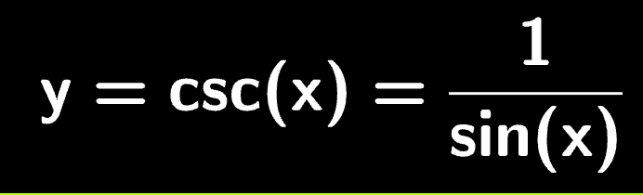

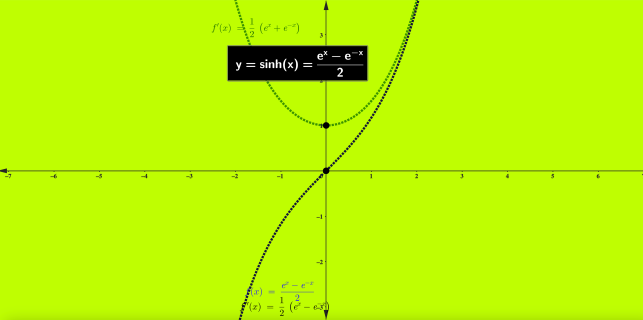














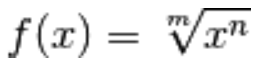

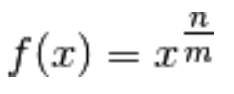





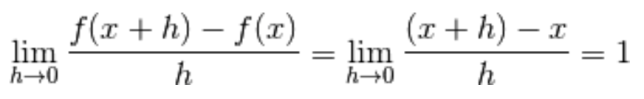
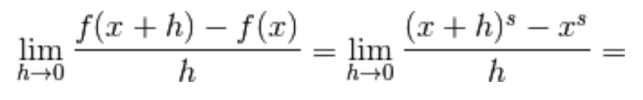


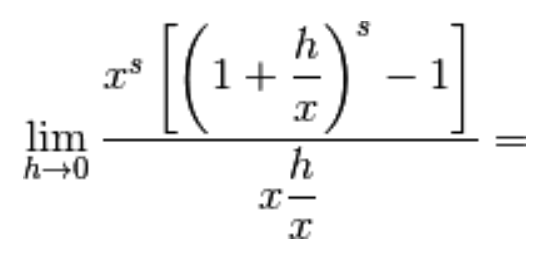

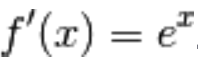

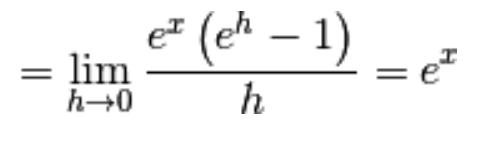



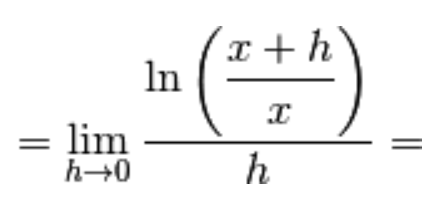

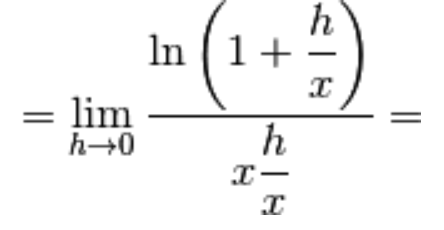
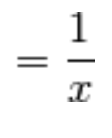
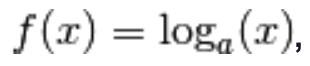



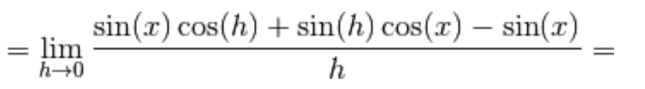


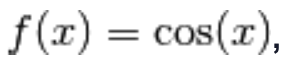

Devi effettuare l'accesso per postare un commento.