Salvatore Di Lucia
Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)
Derivata della funzione composta
Per calcolare la derivata di una funzione qualsiasi ci mancano due strumenti. In questa lezione ci occupiamo del primo: è
il teorema di derivazione della funzione composta.
Questo risultato teorico ha una grande importanza nella risoluzione degli esercizi, perché il 99% delle funzioni che dovremo derivare sono composte.
Nella lezione sull’Algebra delle derivate abbiamo visto qual è la relazione tra la derivazione e le operazioni tra funzioni;
nella tabella delle derivate notevoli, invece, abbiamo visto come calcolare le derivate delle principali funzioni mediante la definizione.
Tenetele a mente prima di proseguire nella lettura.
Indice
-
Teorema
-
Esempio
-
Con tre o più funzioni
-
Dimostrazione
Teorema per la derivata della funzione composta
Il teorema della derivata della funzione composta,
detto anche Regola di Derivazione,
stabilisce che
la derivata di una funzione composta
si calcola come prodotto tra
la derivata della funzione esterna
e
la derivata della funzione interna;
è una regola che permette di calcolare
la derivata di una composizione di funzioni
come
prodotti e derivazioni concatenate.
°°°°°
Consideriamo
due funzioni reali di variabile reale y = f(x) e z =g(y);
sia poi
z = h(x) = g(f(x)) la composizione delle due funzioni.
Supponiamo che
e che
g(y) sia derivabile in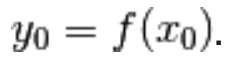 
Vale la seguente formula:
Da un punto di vista operativo,
il teorema permette di calcolare la derivata composta come funzione:
Se preferite, possiamo anche esprimere la formula come:
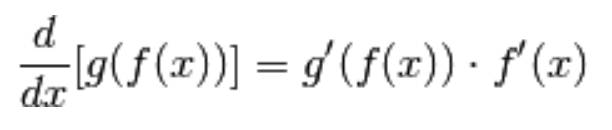
In parole povere,
la derivata della funzione composta 
è data
dalla derivata della funzione più esterna, con argomento invariato, moltiplicata per la derivata della funzione più interna.
Con “funzione più esterna”
si intende l’ultima funzione che interviene nella composizione, g(y),
con funzione “più interna”
si intende la prima funzione che si considera nella composizione, f(x).
Esempio
sulla derivazione della funzione composta
Data la funzione z = h(x), definita come:
Abbiamo
come funzione più esterna:
come funzione più interna: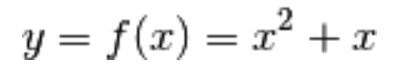
Calcoliamo le derivate separatamente.
Abbiamo
la derivata del logaritmo : 
la derivata di una somma:
Ricordiamoci che è y = f(x):
Il teorema della derivata composta ci dice che
la derivata h'(x) è data da:
°°°°°
Un modo semplice per capire
la logica della derivazione delle funzioni composte è questa:
immaginiamo che la funzione composta da derivare sia un’arancia.
Il teorema stabilisce che prima bisogna derivare la “buccia”
mantenendo la “polpa” invariata,
dopodiché si moltiplica il tutto per la derivata della “polpa”.
°°°°°
Derivazione di più funzioni composte
Il teorema si estende anche al caso di composizioni di tre o più funzioni.
Ad esempio,
nel caso di tre funzioni p(x), q(x), r(x) :
h(x) = r(q(p(x))) ; → h'(x) = r'(q(p(x)))·q'(p(x))·p'(x)
Si procede allo stesso modo nel caso di n funzioni composte tra loro:
si parte derivando la funzione più esterna
(l’ultima in ordine di composizione)
e se ne mantiene l’argomento invariato.
Poi, si passa al livello successivo:
si dimentica la funzione appena derivata,
si deriva la funzione successiva e se ne mantiene l’argomento invariato.
Si moltiplicano tutte le derivate ottenute e si procede così fino alla funzione più interna, ossia la prima in ordine di composizione.
Esempio
Deriviamo la seguente funzione:
Notiamo che
h(x) è la composizione di tre funzioni, h(x) = r(q(p(x))), dove:
Calcoliamo le tre derivate separatamente
(ricordando qual è la derivata del seno):
Applichiamo il teorema:
Nota bene
Quando in una composizione di funzioni ci si riferisce
all’ultima funzione in ordine di composizione
si intende la prima funzione che si scrive.
Ad esempio,
in f(x) = Z(W(…(A(X))))
l’ultima funzione in ordine di composizione è Z, è la prima da derivare.
La prima funzione in ordine di composizione è A, è l’ultima da derivare.
Dimostrazione
del teorema di derivazione della funzione composta
Diamo la dimostrazione nel caso di due funzioni,
siano z = g(y) e y = f(x),
cosicché
la funzione composta è z = h(x) = g(f(x)).
Nel caso di più funzioni composte si ragiona in modo analogo.
Usiamo la definizione di derivata
e
calcoliamo il limite del rapporto incrementale in 
per la funzione h(x).
Obiettivo:
provare che
il limite esiste finito e che si calcola con la formula dell’enunciato.
Scriviamo espressamente h(x) come funzione composta:
moltiplichiamo e dividiamo la frazione per 
.
Ora ricordiamo che f(x) = y e che 
Inoltre è chiaro che al tendere di 
anche 
ossia che 
Questo perché
la funzione f è derivabile in ,
e
in quanto tale è anche ivi continua.
Grazie a queste considerazioni,
e a una semplice regola dell’Algebra dei limiti:
(il limite di un prodotto é uguale al prodotto dei limiti)
possiamo calcolare:
La funzione g(y) è derivabile in 
per ipotesi,
dunque
il primo limite esiste e vale 
discorso analogo
per f(x), che è derivabile in .
il secondo limite esiste e vale
Ricordiamo infine che 
, e la dimostrazione è conclusa.
Anche se all’inizio la tecnica di derivazione della funzione composta può apparire impegnativa, dopo una pò di esercizi risulta molto più semplice.
°°°°°
iMathematica 
Devi effettuare l'accesso per postare un commento.