
Salvatore Di Lucia


Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)



Teorema di Fermat:
1.) enunciato,
2.) dimostrazione,
3.) utilizzi.
Entriamo nel vivo della questione e introduciamo un risultato che si rivelerà molto importante:
il teorema di Fermat.
Ancora prima di enunciarlo,
vi anticipiamo che ci permetterà di individuare
i candidati punti di massimo e minimo relativo per le funzioni,
che abbiamo definito nella lezione precedente.
Indice
1.) Punti critici e punti stazionari
2.) Teorema di Fermat
3.) A cosa serve
Definizioni preliminari:
1.) punti critici e punti stazionari
Prima di enunciare il teorema e spiegare a cosa serve, ci servono due definizioni preliminari.
Consideriamo
una funzione reale di variabile reale y = f(x),
sia
Dom(f) il suo dominio
e supponiamo che
f(x) sia continua sul proprio dominio.
Diciamo che
 , interno al dominio, è un punto critico della funzione
, interno al dominio, è un punto critico della funzione
se soddisfa una delle seguenti condizioni:
I.)  è un punto di non derivabilità della funzione;
è un punto di non derivabilità della funzione;
II.)  è un punto in cui la funzione è derivabile
è un punto in cui la funzione è derivabile
e in cui la derivata è nulla:  .
.
Nel secondo caso diciamo che  è un punto stazionario della funzione.
è un punto stazionario della funzione.
Da queste semplici definizioni si vede che
un punto stazionario è anche un punto critico,
e che
un punto critico non è necessariamente un punto stazionario.

Il teorema di Fermat per le derivate stabilisce che
una funzione che ammette un massimo o un minimo relativo in un punto interno del dominio, e che sia ivi derivabile,
ha la derivata prima nulla nel punto.
In termini formali:
sia y = f(x) una funzione con dominio Dom(f).
Se un punto interno  è un punto di massimo o minimo relativo per f,
è un punto di massimo o minimo relativo per f,
e
se la funzione è derivabile in  ,
,
allora
si ha che  In modo equivalente:
In modo equivalente:
un punto interno al dominio, estremante per la funzione
e
di derivabilità per la funzione, è un punto stazionario per la funzione.
Ricordiamoci che
i punti estremanti assoluti sono anche relativi
(il viceversa in generale non è vero),
quindi il teorema contempla anche
il caso dei punti di massimo e punti di minimo assoluti.
Dimostrazione
Dimostriamo
il teorema nel caso in cui  è un punto di massimo relativo;
è un punto di massimo relativo;
per i punti di minimo relativo varranno considerazioni analoghe.
Prima di tutto:
 è un punto interno del dominio,
è un punto interno del dominio,
quindi
esiste almeno un intorno interamente contenuto nel dominio.
interamente contenuto nel dominio.
Usiamo
la definizione di punto di massimo relativo, secondo cui
esiste almeno un intorno  tale che
tale che  per ogni
per ogni 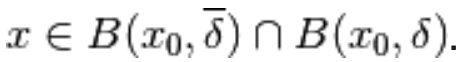 .
.
L’intersezione ci assicura di rimanere nel dominio: chiamiamola B.
Noi vogliamo dimostrare che  quindi dobbiamo passare per
quindi dobbiamo passare per
la definizione di derivata come limite del rapporto incrementale.
Cerchiamo di ricostruirlo e riscriviamo
la condizione di punto di massimo relativo in una forma più pratica:

La condizione, a maggior ragione, vale se escludiamo il punto  :
:

In questo modo la differenza 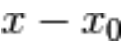 è sicuramente diversa da zero.
è sicuramente diversa da zero.
Distinguiamo due casi.
1,) Per  se dividiamo per
se dividiamo per 
abbiamo:
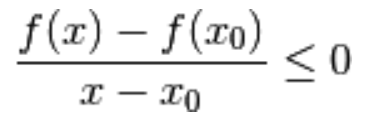
2.) Per  se dividiamo per
se dividiamo per 
dobbiamo invertire il simbolo di disuguaglianza:
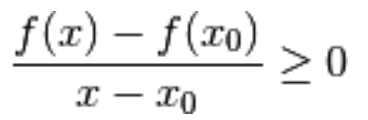
Se passiamo al limite per  in entrambe le disuguaglianze, otteniamo:
in entrambe le disuguaglianze, otteniamo:


Scriviamoli in una forma equivalente e più familiare:

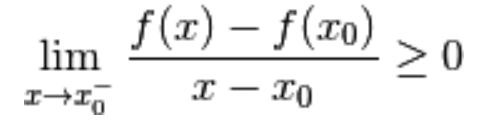
I due limiti sono rispettivamente
la derivata sinistra e la derivata destra nel punto:
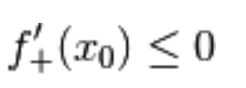

Per l’ipotesi di derivabilità di f in  i due valori devono esistere finiti e, nello specifico, essere uguali.
i due valori devono esistere finiti e, nello specifico, essere uguali.
L’unico caso possibile è:
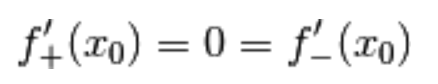
Ossia
 , cioè la tesi.
, cioè la tesi.
°°°°°
3.) A cosa serve il teorema di Fermat?
L’enunciato esprime
una condizione sufficiente per l’annullamento della derivata prima;
leggiamolo al contrario e ricaviamone una condizione necessaria.
L’annullamento della derivata prima di una funzione derivabile in un punto  interno al dominio è condizione necessaria affinché
interno al dominio è condizione necessaria affinché
 sia un punto di massimo o di minimo relativo per la funzione.
sia un punto di massimo o di minimo relativo per la funzione.
Nella pratica, dunque,
il teorema di Fermat ci dice che i punti interni al dominio in cui si annulla la derivata sono i candidati punti di massimo o di minimo della funzione;
“candidati” proprio perché la condizione è necessaria ma non sufficiente.
Attenzione
perché
questo criterio si riferisce solo ai punti interni al dominio in cui la funzione è derivabile;
come vedremo in seguito,
i punti di non derivabilità e gli eventuali estremi finiti del dominio
vanno analizzati a parte per capire se sono
punti di massimo, punti di minimo o nessuno dei due.
Nelle lezioni successive passeremo ai risultati teorici e al metodo pratico per calcolare i punti di massimo e minimo, di distinguerne la natura
(il tipo: max o min)
e
di studiare la monotonia delle funzioni,
cioè il comportamento sul dominio.
°°°°°

Tag: teorema di Fermat

Salvatore Di Lucia


Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)



Massimi e minimi relativi e assoluti
Questa lezione è il punto di partenza per
lo studio di massimi e minimi
e
della monotonia (crescita e decrescita) delle funzioni,
e viene trattato nel dettaglio qui e nelle lezioni successive.
Studiamo
le definizioni preliminari su massimi e minimi relativi e assoluti,
che riprenderemo nel seguito.
Tenete conto che
lo studio dei massimi e dei minimi
è il cuore
della teoria delle derivate
e che trova la sua principale applicazione nello
studio di funzione.
Per comprendere a fondo l’argomento è importante avere dimestichezza con i tipi di monotonia delle funzioni; nel caso, vi suggeriamo un ripasso tattico.
Indice
-
Definizioni
-
Esempio
-
Relazione
-
Caratterizzazione
Cosa sono i massimi e i minimi di una funzione?
I massimi e minimi relativi e assoluti di una funzione
sono rispettivamente
i massimi e i minimi valori che la funzione assume
localmente o globalmente;
le ascisse corrispondenti vengono dette
punti di massimo e di minimo (relativi o assoluti).
Uno dei principali utilizzi delle derivate, in Analisi Matematica,
è studiare alcuni aspetti qualitativi delle
funzioni reali di variabile reale f : Dom⊆R→R,
individuate da un’espressione analitica y = f(x).
Sapendo calcolare le derivate avremo un procedimento che ci permetterà di studiare una qualsiasi funzione derivabile per:
– trovare tutti i massimi e i minimi, sia relativi che assoluti;
– stabilire in quali intervalli la funzione cresce o decresce.
Per riuscirci dobbiamo prima conoscere
le definizioni rigorose di massimo e minimo relativo e assoluto.
°°°°°
1.) 
Sia y = f(x) una funzione con dominio Dom(f).
Diciamo che
 è un punto di massimo assoluto per la funzione,
è un punto di massimo assoluto per la funzione,
e che
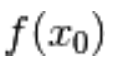 è il massimo assoluto della funzione,
è il massimo assoluto della funzione,
se per ogni  risulta che
risulta che 
Osservazione:
nella definizione
 è un punto di massimo,
è un punto di massimo,
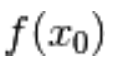 il valore massimo assoluto.
il valore massimo assoluto.
A uno o più punti di massimo assoluto corrisponde il massimo valore assoluto.
2.) 
Sia y = f(x) una funzione con dominio Dom(f).
che
 è un punto di minimo assoluto per la funzione,
è un punto di minimo assoluto per la funzione,
e che
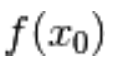 è il minimo assoluto della funzione,
è il minimo assoluto della funzione,
se per ogni  risulta che
risulta che 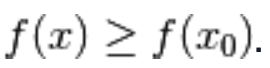
°°°°°
Riguardo alla distinzione tra
punto di massimo assoluto e punto di minimo assoluto,
vale un’osservazione analoga alla precedente.
Significato di assoluto
In parole povere
un punto di massimo assoluto è un’ascissa che realizza, mediante la funzione, il massimo tra tutti i valori assunti da f;
un punto di minimo assoluto è un’ascissa che realizza, mediante la funzione, il minimo tra tutti i valori assunti da f.
°°°°°
La condizione di
 come punto di massimo assoluto per la funzione se:
come punto di massimo assoluto per la funzione se:
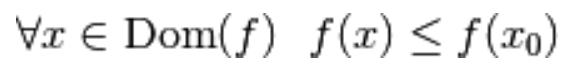
Analogamente
diciamo che
 è un punto di minimo assoluto per la funzione se:
è un punto di minimo assoluto per la funzione se:
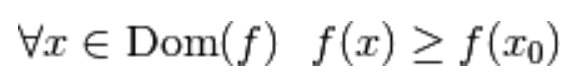
3.) 
Sia y = f(x) una funzione con dominio Dom(f).
Diciamo che
 è un punto di massimo relativo per la funzione
è un punto di massimo relativo per la funzione
se esiste almeno un intorno  di raggio δ e centro
di raggio δ e centro  tale che per ogni x appartenente a
tale che per ogni x appartenente a 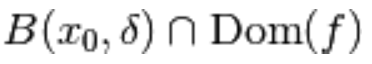 risulta che
risulta che 
4.) 
Sia y = f(x) una funzione con dominio Dom(f).
Diciamo che
 è un punto di minimo relativo per la funzione
è un punto di minimo relativo per la funzione
se esiste almeno un intorno  di raggio δ e centro
di raggio δ e centro  tale che per ogni x appartenente a
tale che per ogni x appartenente a 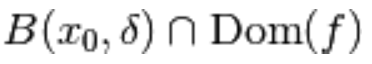 risulta che
risulta che 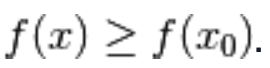 .
.
°°°°°

In altri termini
un punto è di massimo relativo se esiste un intorno di tale punto in cui il valore della funzione nel punto è il massimo valore tra quelli assunti dalla funzione nell’intorno.
In modo analogo
un punto é di minimo relativo se esiste un intorno di tale punto in cui il valore della funzione nel punto è il minimo valore tra quelli assunti dalla funzione nell’intorno.
Potrebbe sembrare uno scioglilingua, quindi cerchiamo di esprimerci in modo più sintetico:
un punto di massimo o un punto di minimo è relativo
se determina localmente
il massimo valore o il minimo valore di ordinata della funzione.
Attenzione, inoltre,
a un aspetto della definizione che potrebbe passare inosservato.
L’intorno non deve essere tutto contenuto nel dominio,
ma la condizione sui valori della funzione deve valere
per tutti i punti appartenenti all’intorno e in cui la funzione è definita.
Esempio generale
Tutto questo sembra complicato, ma non lo è.
Consideriamo la funzione rappresentata in figura,
tenendo conto che il grafico non prosegue oltre l’intervallo in cui è disegnato.

I punti evidenziati in nero sull’asse delle ascisse sono rispettivamente:
un punto di massimo relativo, un punto di minimo relativo,
un punto di massimo assoluto, un punto di minimo assoluto.
Le corrispondenti ordinate sono rispettivamente:
un massimo relativo, un minimo relativo,
un massimo assoluto, un minimo assoluto.
Come caso particolare,
se immaginiamo che
la funzione sia definita negli estremi sinistro e destro dell’intervallo,
allora tali punti sono rispettivamente di minimo relativo e di massimo relativo;
da notare che in questo caso la definizione si adatta all’esistenza di un intorno solo destro o solo sinistro.
Se invece immaginiamo che
i due estremi non siano inclusi nell’intervallo di definizione,
allora… non sono nulla.
Per completezza,
i punti di massimo e minimo vengono detti punti estremanti della funzione,
indipendentemente che siano relativi o assoluti.
Relazione tra massimi e minimi relativi e assoluti
Osserviamo che
un massimo (o un minimo) assoluto di una funzione
è anche
un massimo (o un minimo) relativo;
al contrario
un massimo (o un minimo) relativo
non è necessariamente un massimo (o un minimo) assoluto.
La traduzione di quest’ultima frase in matematica è:
1.) relativo è condizione necessaria ma non sufficiente per assoluto;
2.) assoluto è condizione sufficiente ma non necessaria per relativo.
°°°°°
Caratterizzazione per massimi e minimi nel caso di funzioni continue
Se vogliamo darne una caratterizzazione dal punto di vista pratico,
possiamo affermare che:
1.) Affinché  sia un punto di massimo relativo per la funzione f,
sia un punto di massimo relativo per la funzione f,
è necessario che la funzione f(x) sia
crescente o non decrescente a sinistra di 
e
decrescente o non crescente a destra di  .
.
2.) Affinché  sia un punto di minimo relativo per la funzione f,
sia un punto di minimo relativo per la funzione f,
è necessario che la funzione f(x) sia
decrescente o non crescente a sinistra di 
e
crescente o non decrescente a destra di  .
.
Per il momento niente esercizi correlati, ci serve ancora un po’ di teoria.
Nella lezione successiva vedremo
un teorema fondamentale per lo studio dei punti di massimo e minimo delle funzioni reali di variabile reale:
Un teorema semplice, ma molto importante.
°°°°°

Tag: Massimi e minimi relativi e assoluti

Salvatore Di Lucia


Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)



Derivata della funzione inversa
Ora che conosciamo
il primo dei due teoremi fondamentali sul calcolo delle derivate
(derivata della funzione composta),
passiamo a studiare il secondo:
il teorema di derivazione della funzione inversa.
Per capire il significato e l’utilità del teorema è necessario avere un’idea chiara su cos’è l’inversa di una funzione.
In questa lezione ne diamo un cenno, ma in caso di dubbi vi invitiamo a leggere la lezione di riferimento: inversa di una funzione.
Indice :
-
Premessa
-
Teorema
-
Esempio
-
Dimostrazione
°°°°°
1.) Premessa: a proposito della funzione inversa
Sia
y = f(x) una funzione reale di variabile reale con dominio Dom(f),
e supponiamo che
y = f(x) sia biunivoca, ossia iniettiva e suriettiva.
Allora
esiste una funzione inversa,
vale a dire
una funzione x = g(y) tale che g(f(x)) = x.
L’inversa di una funzione f si indica con 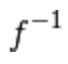
e stabilisce proprio
la corrispondenza inversa rispetto all’associazione definita da y = f(x),
in modo che
la composizione delle due funzioni si riduca alla funzione identità su Dom(f),
ossia 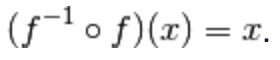
°°°°°
2.) Teorema di derivazione della funzione inversa
Il teorema per la derivata della funzione inversa è un risultato teorico
che permette di
calcolare la derivata dell’inversa di una funzione in un punto
senza
conoscere l’espressione analitica dell’inversa.
Enunciato.
Consideriamo
una funzione y=f(x) invertibile, derivabile in un punto 
e
supponiamo che
f(x) abbia derivata diversa da zero nel punto: 
Allora
la funzione inversa  è derivabile nel punto
è derivabile nel punto 
e la sua derivata in tale punto è: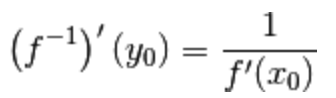
L’enunciato può sembrare difficile,
ma analizzandolo si vede subito che non lo è.
Per ipotesi la funzione f deve essere invertibile,
dunque tale da ammettere una funzione inversa 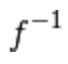 ;
;
deve essere derivabile in un punto  del suo dominio e
del suo dominio e
la derivata in tale punto deve essere diversa da zero:  .
.
Sotto queste condizioni, la tesi fornisce due informazioni:
I.) la funzione inversa 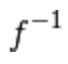 è derivabile nell’immagine del punto
è derivabile nell’immagine del punto  mediante f, ossia in
mediante f, ossia in 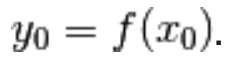
II.) sappiamo anche come
calcolare la derivata della funzione inversa 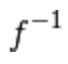 nel punto
nel punto  ,
,
ossia come
reciproco della derivata della funzione f nel punto  .
.
Qualcuno potrebbe confondersi leggendo le parole tra simboli e punti, ma la seguente immagine dovrebbe chiarire le idee.

Per quale motivo il teorema è utile?
Perché
ci permette di calcolare la derivata di una funzione – l’inversa – senza bisogno di derivarla.
Inoltre,
nonostante il teorema fornisca un criterio di calcolo della derivata dell’inversa in un punto,
possiamo conoscere in automatico la derivata dell’inversa come funzione:
è sufficiente applicare la formula del teorema considerando un punto generico.
Esempio
di derivazione della funzione inversa
Se siete interessati a esempi numerici, al termine della lezione vi suggeriamo di leggere la scheda correlata di esercizi risolti.
Qui vediamo un esempio un po’ più fine,
utile per mostrare l’importanza del teorema.
3.) Esempio:
usare il Teorema di derivazione della funzione inversa per dimostrare che
Svolgimento:
consideriamo la funzione logaritmica f(x) = ln (x), e non a caso.
Il suo dominio è Dom (f) = (0,+∞),
è biunivoca,
è derivabile su tutto il suo dominio.
Conosciamo la funzione inversa della funzione logaritmica,
che è proprio l’esponenziale: 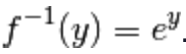 .
.
Infatti:

Sappiamo che la derivata del logaritmo è:
Usiamo il teorema di derivazione della funzione inversa,
considerando  come un generico punto.
come un generico punto.
Possiamo farlo perché la derivata f'(x) non si annulla in alcun punto del dominio, quindi le ipotesi del teorema sono soddisfatte.
La tesi ci dice che
la derivata dell’inversa nel punto 
è il reciproco della derivata 
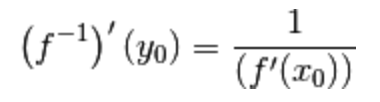
Poiché è 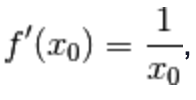 , sostituiamolo nell’uguaglianza:
, sostituiamolo nell’uguaglianza:
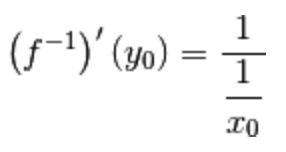
Poiché è  , possiamo scrivere:
, possiamo scrivere:
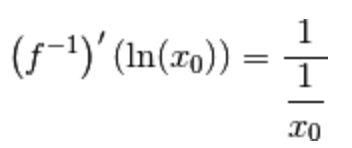
A destra dell’uguale possiamo usare la regola per le frazioni di frazioni:

Cosa abbiamo scoperto?
Che
 è quella funzione che, applicata al logaritmo
è quella funzione che, applicata al logaritmo 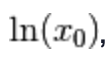 , dà
, dà  .
.
Quindi,
per la generalità del punto 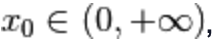 , abbiamo scoperto che anche
, abbiamo scoperto che anche deve comportarsi come inversa della funzione ln (x).
deve comportarsi come inversa della funzione ln (x).
In sintesi:
il teorema ci ha permesso di calcolare
la derivata dell’inversa di f(x) = ln (x),
ossia
la derivata della funzione esponenziale 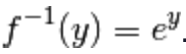
Questa derivata deve comportarsi come inversa del logaritmo,
quindi deve essere a sua volta l’esponenziale:

E abbiamo trovato che
la derivata dell’esponenziale è l’esponenziale stessa.
°°°°°
4.) Dimostrazione
del teorema per la derivata della funzione inversa
Concludiamo con la dimostrazione del teorema.
Dato che vogliamo ricavare
la formula per la derivata dell’inversa in un punto, facciamo riferimento
alla definizione di derivata come limite del rapporto incrementale.
Per ipotesi
la funzione inversa  esiste,
esiste,
perché 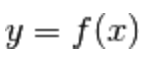 è invertibile.
è invertibile.
Consideriamo il limite del rapporto incrementale della funzione inversa centrato nel punto 
Quest’ultimo è l’immagine di un punto  in cui la funzione
in cui la funzione  è derivabile con derivata diversa da zero:
è derivabile con derivata diversa da zero:  .
.
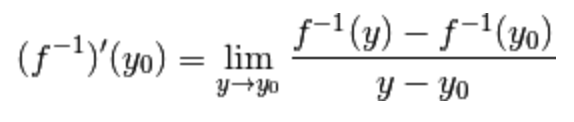
Vogliamo
dimostrare che questo limite esiste finito e che è uguale al reciproco di  .
.
Riscriviamolo esprimendo tutto nella variabile x, ma facciamolo con cautela.
Dire che  significa che
significa che  : ciò implica che
: ciò implica che  ?
?
Sì, perché f(x) è una funzione derivabile in  ,
,
dunque è anche continua in  .
.
Dai teoremi sulla continuità anche
l’inversa deve essere continua nell’immagine 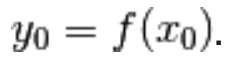 ,
,
ossia
al tendere di  risulta che
risulta che 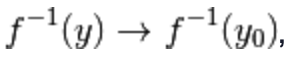 ,
,
e questo significa che  .
.
Possiamo allora riscrivere
il limite del rapporto incrementale
come:

Per definizione di funzione inversa,
risulta che
e che .
.
Ciò ci permette di esprimere
il limite del rapporto incrementale
nel seguente modo:
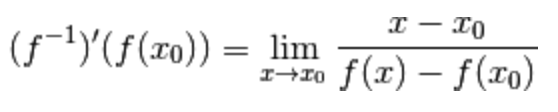
Osserviamo attentamente il limite appena scritto.
Esso non è altro che il reciproco del rapporto incrementale associato alla funzione f(x) e centrato in  :
:
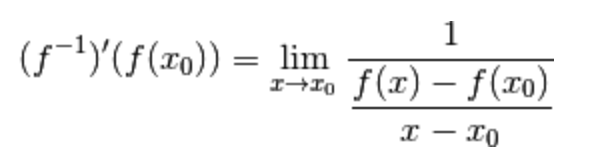
Per ipotesi la funzione f(x) è derivabile in  ,
,
dunque esiste ed è finito il limite:

A questo punto facciamo intervenire l’Algebra dei limiti
e l’ipotesi per cui  , così che esiste finito il limite:
, così che esiste finito il limite:

Di conseguenza
la funzione  è derivabile in
è derivabile in  ,
,
e la derivata in tale punto vale:
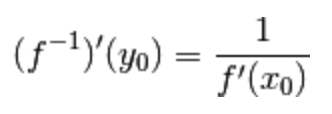
Ossia la tesi.
Nella scheda correlata di esercizi svolti ci concentriamo sull’applicazione pratica del teorema, ossia come calcolare la derivata della funzione inversa in uno specifico punto.
°°°°°

Tag: Derivata della funzione inversa

Salvatore Di Lucia


Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)



Derivata della funzione composta
Per calcolare la derivata di una funzione qualsiasi ci mancano due strumenti. In questa lezione ci occupiamo del primo: è
il teorema di derivazione della funzione composta.
Questo risultato teorico ha una grande importanza nella risoluzione degli esercizi, perché il 99% delle funzioni che dovremo derivare sono composte.
Nella lezione sull’Algebra delle derivate abbiamo visto qual è la relazione tra la derivazione e le operazioni tra funzioni;
nella tabella delle derivate notevoli, invece, abbiamo visto come calcolare le derivate delle principali funzioni mediante la definizione.
Tenetele a mente prima di proseguire nella lettura.
Indice
-
Teorema
-
Esempio
-
Con tre o più funzioni
-
Dimostrazione
Teorema per la derivata della funzione composta
Il teorema della derivata della funzione composta,
detto anche Regola di Derivazione,
stabilisce che
la derivata di una funzione composta
si calcola come prodotto tra
la derivata della funzione esterna
e
la derivata della funzione interna;
è una regola che permette di calcolare
la derivata di una composizione di funzioni
come
prodotti e derivazioni concatenate.
°°°°°
Consideriamo
due funzioni reali di variabile reale y = f(x) e z =g(y);
sia poi
z = h(x) = g(f(x)) la composizione delle due funzioni.
Supponiamo che
e che
g(y) sia derivabile in 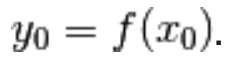
Vale la seguente formula:

Da un punto di vista operativo,
il teorema permette di calcolare la derivata composta come funzione:

Se preferite, possiamo anche esprimere la formula come:
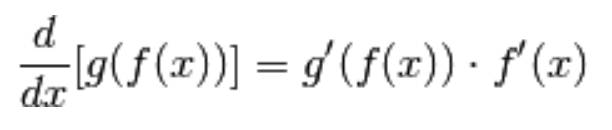
In parole povere,
la derivata della funzione composta  è data
è data
dalla derivata della funzione più esterna, con argomento invariato, moltiplicata per la derivata della funzione più interna.
Con “funzione più esterna”
si intende l’ultima funzione che interviene nella composizione, g(y),
con funzione “più interna”
si intende la prima funzione che si considera nella composizione, f(x).
Esempio
sulla derivazione della funzione composta
Data la funzione z = h(x), definita come: Abbiamo
Abbiamo
come funzione più esterna:
come funzione più interna: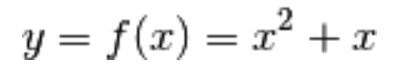
Calcoliamo le derivate separatamente.
Abbiamo
la derivata del logaritmo : 
la derivata di una somma:
Ricordiamoci che è y = f(x):

Il teorema della derivata composta ci dice che
la derivata h'(x) è data da:


°°°°°
Un modo semplice per capire
la logica della derivazione delle funzioni composte è questa:
immaginiamo che la funzione composta da derivare sia un’arancia.
Il teorema stabilisce che prima bisogna derivare la “buccia”
mantenendo la “polpa” invariata,
dopodiché si moltiplica il tutto per la derivata della “polpa”.
°°°°°
Derivazione di più funzioni composte
Il teorema si estende anche al caso di composizioni di tre o più funzioni.
Ad esempio,
nel caso di tre funzioni p(x), q(x), r(x) :
h(x) = r(q(p(x))) ; → h'(x) = r'(q(p(x)))·q'(p(x))·p'(x)
Si procede allo stesso modo nel caso di n funzioni composte tra loro:
si parte derivando la funzione più esterna
(l’ultima in ordine di composizione)
e se ne mantiene l’argomento invariato.
Poi, si passa al livello successivo:
si dimentica la funzione appena derivata,
si deriva la funzione successiva e se ne mantiene l’argomento invariato.
Si moltiplicano tutte le derivate ottenute e si procede così fino alla funzione più interna, ossia la prima in ordine di composizione.
Esempio
Deriviamo la seguente funzione:

Notiamo che
h(x) è la composizione di tre funzioni, h(x) = r(q(p(x))), dove:

Calcoliamo le tre derivate separatamente
(ricordando qual è la derivata del seno):

Applichiamo il teorema:

Nota bene
Quando in una composizione di funzioni ci si riferisce
all’ultima funzione in ordine di composizione
si intende la prima funzione che si scrive.
Ad esempio,
in f(x) = Z(W(…(A(X))))
l’ultima funzione in ordine di composizione è Z, è la prima da derivare.
La prima funzione in ordine di composizione è A, è l’ultima da derivare.
Dimostrazione
del teorema di derivazione della funzione composta
Diamo la dimostrazione nel caso di due funzioni,
siano z = g(y) e y = f(x),
cosicché
la funzione composta è z = h(x) = g(f(x)).
Nel caso di più funzioni composte si ragiona in modo analogo.
Usiamo la definizione di derivata
e
calcoliamo il limite del rapporto incrementale in  per la funzione h(x).
per la funzione h(x).
Obiettivo:
provare che
il limite esiste finito e che si calcola con la formula dell’enunciato.

Scriviamo espressamente h(x) come funzione composta:
 moltiplichiamo e dividiamo la frazione per
moltiplichiamo e dividiamo la frazione per  .
.

Ora ricordiamo che f(x) = y e che 
Inoltre è chiaro che al tendere di  anche
anche 
ossia che 
Questo perché
la funzione f è derivabile in  ,
,
e
in quanto tale è anche ivi continua.
Grazie a queste considerazioni,
e a una semplice regola dell’Algebra dei limiti:
(il limite di un prodotto é uguale al prodotto dei limiti)
possiamo calcolare:

La funzione g(y) è derivabile in  per ipotesi,
per ipotesi,
dunque
il primo limite esiste e vale 
discorso analogo
per f(x), che è derivabile in  .
.
il secondo limite esiste e vale

Ricordiamo infine che  , e la dimostrazione è conclusa.
, e la dimostrazione è conclusa.

Anche se all’inizio la tecnica di derivazione della funzione composta può apparire impegnativa, dopo una pò di esercizi risulta molto più semplice.
°°°°°

Tag: Derivata della funzione composta

Salvatore Di Lucia


Georg Friedrich Bernard Riemann
°°°°°
“Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.“
(John von Neumann)



Calcolo delle derivate: regole di derivazione
Se si conoscono le derivate delle funzioni elementari,
l’Algebra delle derivate è la base che permette di calcolare
la derivata di una qualsiasi funzione
in cui sono presenti
somme e differenze, prodotti e rapporti di funzioni.
Per l’elevamento a potenza ci servirà invece
il teorema per la derivata della funzione composta,
di cui parleremo nella prossima lezione;
per la funzione inversa ci servirà invece
il teorema per la derivata della funzione inversa.
Indice
1.) Regole di derivazione
2.) Esempi
1.) Regole di derivazione per il calcolo delle derivate
Il calcolo delle derivate è un procedimento che si basa su un insieme di regole,
dette
regole di derivazione,
che descrivono il comportamento della derivazione rispetto alle operazioni algebriche tra funzioni:
prodotto per una costante,
somma e differenza,
prodotto e rapporto.
Ognuna delle seguenti regole si dimostra usando
la definizione di derivata.
1.) La derivata del prodotto di una costante per una funzione
è uguale
alla costante per la derivata della funzione.
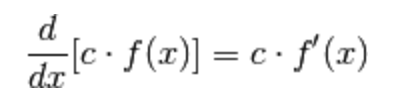
Ogni volta che abbiamo un coefficiente che moltiplica una funzione,
se dobbiamo derivare il tutto,
basta riscrivere il coefficiente e derivare solamente la funzione.
2.) La derivata di una somma o differenza di funzioni
è uguale
alla somma o differenza delle singole derivate.

Dunque se dobbiamo derivare una somma o una differenza di funzioni,
ci basterà derivare i singoli addendi.
Vi facciamo notare che la regola fa riferimento alla somma algebrica,
intesa quindi come addizione o sottrazione.
Si procede in modo analogo nel caso della somma o differenza di tre o più funzioni.
3.) La derivata del prodotto di due funzioni
è uguale
alla prima funzione derivata per la seconda più la prima funzione per la derivata della seconda.

Nel caso del prodotto di tre o più funzioni vale una regola analoga, che si ottiene considerando due fattori come un’unica funzione e reiterando la formula.

Per approfondire:







°°°°°
4.) La derivata del rapporto di due funzioni
è uguale
al rapporto tra la derivata del numeratore per il denominatore
meno il numeratore per la derivata del denominatore,
tutto fratto il denominatore al quadrato.

Per approfondire:






°°°°°
Per i più esperti che stanno leggendo questo articolo,
le prime due regole si riassumono dicendo che
l’operatore di derivazione D : f → f’ è lineare e omogeneo.
°°°°°
Esempi di calcolo delle derivate
Prima di procedere è bene sapere quali sono
le derivate fondamentali,
perlomeno per le funzioni più ricorrenti.
1.) Data la funzione

per la regola di derivazione del prodotto costante-funzione abbiamo che:
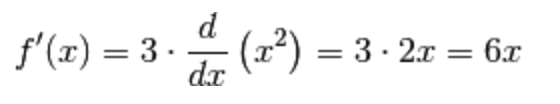
2.) Data la funzione

dalla regola di derivazione della differenza di funzioni risulta:

3.) Data la funzione

per la regola di derivazione del prodotto di funzioni:


4.) Data la funzione

per la regola di derivazione del rapporto di funzioni risulta:

Qui basta ricordare le espressioni per la derivata di una potenza e per la derivata del coseno:
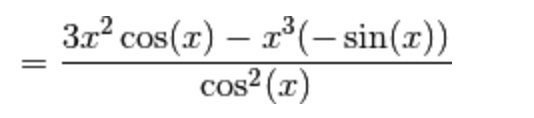
°°°°°
Esempio misto con applicazione di più regole
Vediamo un esempio in cui dobbiamo applicare più regole di derivazione. Consideriamo la seguente funzione e calcoliamone la derivata.
1.) 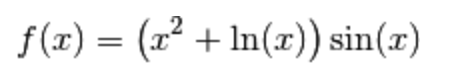
In accordo con le regole sull’ordine delle operazioni prima si effettuano i prodotti e poi le somme, quindi prima di tutto applichiamo la regola di derivazione del prodotto:
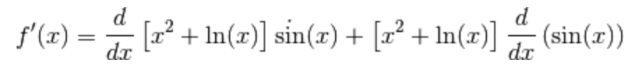
Al primo addendo applichiamo la regola di derivazione della somma di funzioni:

Infine, grazie alla tabella delle derivate delle funzioni elementari:

L’aspetto importante dell’esempio riguarda
l’ordine da seguire nei vari livelli di derivazione:
è lo stesso delle operazioni algebriche.
Per essere in grado di calcolare qualsiasi derivata ci mancano
i teoremi di derivazione della funzione composta e dell’inversa.
°°°°°

Tag: Calcolo delle derivate: regole di derivazione





 In modo equivalente:
In modo equivalente: quindi dobbiamo passare per
quindi dobbiamo passare per

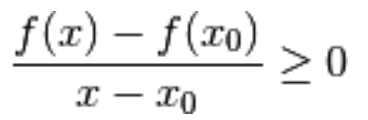


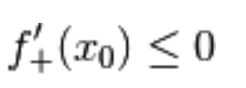
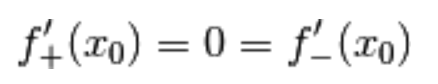
 , cioè la tesi.
, cioè la tesi.



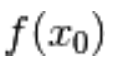 il valore massimo assoluto.
il valore massimo assoluto.
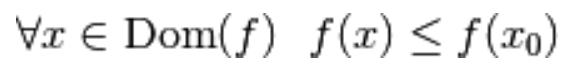
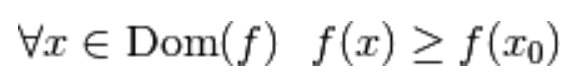






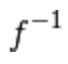 ;
;


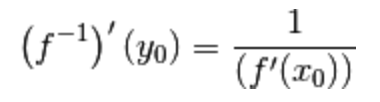
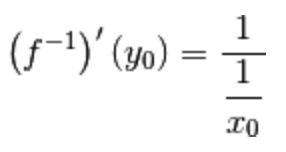
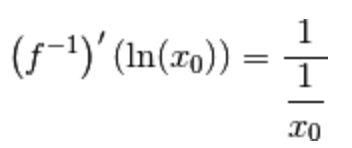


 esiste,
esiste,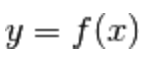 è invertibile.
è invertibile.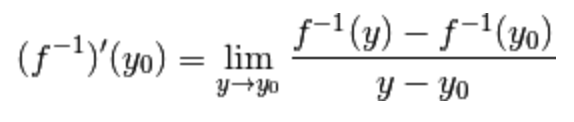

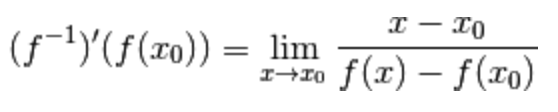
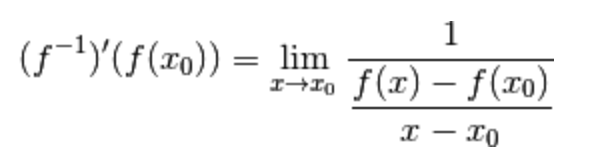


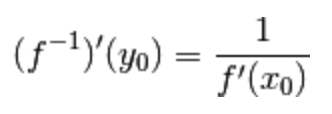




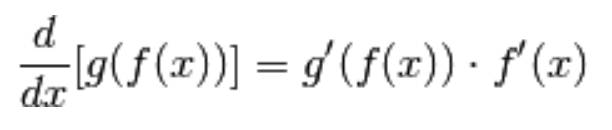
 è data
è data Abbiamo
Abbiamo





 moltiplichiamo e dividiamo la frazione per
moltiplichiamo e dividiamo la frazione per 


 , e la dimostrazione è conclusa.
, e la dimostrazione è conclusa.



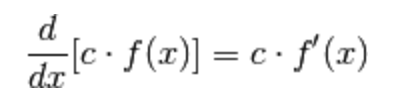






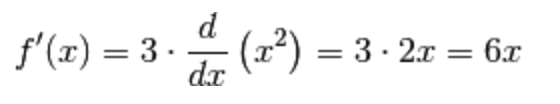







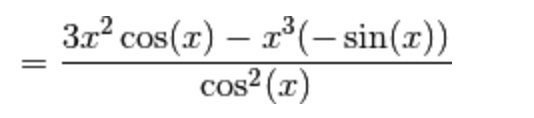
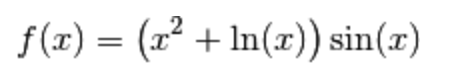
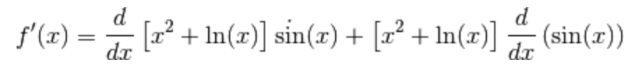


Devi effettuare l'accesso per postare un commento.