

Dal XIII al XIX secolo
Il Pensiero Matematico
La funzione zeta di Riemann.-
Nel suo paper 1859 “sul numero di numeri primi minori di una grandezza data“, Bernhard Riemann ha dato una formula che coinvolge la sua funzione zeta per determinare il numero dei primi minori di un numero specifico
 Questa dimostrazione illustra il comportamento della integrale logaritmica
Questa dimostrazione illustra il comportamento della integrale logaritmica
 che corrisponde ai termini secondo o “periodico”, di cui alla zeta di Riemann.
che corrisponde ai termini secondo o “periodico”, di cui alla zeta di Riemann.
Definizione e prime proprietà.-
La funzione zeta di Riemann è definita come la serie di Dirichlet

Questa restrizione è necessaria affinché la serie risulti convergente, tuttavia la funzione si può prolungare analiticamente a una funzione olomorfa su tutto il piano complesso ad eccezione di 1, dove ha un polo semplice. La funzione zeta possiede zeri semplici negli interi pari negativi, detti zeri banali, mentre tutti gli altri zeri sono disposti simmetricamente rispetto alla retta

detta retta critica, e sono tutti contenuti nella striscia

detta striscia critica.
Osservazione 1
In matematica, una serie di Dirichlet è una qualunque serie della forma

dove s e i coefficienti an sono numeri complessi.
Osservazione 2

Osservazione 3
In matematica, un carattere di Dirichlet modulo k è una funzione aritmetica completamente moltiplicativa che estende a tutti i naturali un carattere del gruppo delle unità di Z/qZ. Più precisamente, dato un intero positivo q, una funzione aritmetica χ(n) si dice essere un carattere modulo q se esiste un omomorfismo f dal gruppo degli invertibili di Z/qZ negli invertibili di C tale che

Se come funzione f si prende la funzione costantemente uguale a 1, allora il carattere χ1 associato ad f è detto carattere principale modulo q.
Se un carattere di Dirichlet modulo q si può scrivere come prodotto di un carattere modulo un intero k strettamente minore di q (che dovrà necessariamente essere un divisore di q) e il carattere principale modulo q, allora esso verrà detto non primitivo. I caratteri che non sono non primitivi, sono detti primitivi.
Proprietà elementari
Dato che per ogni intero positivo q vi sono esattamente φ(q) caratteri di Z/qZ, si ha che lo stesso vale per i caratteri di Dirichlet modulo q.
Inoltre, dalla definizione discende subito che essi sono completamente moltiplicativi, periodici di periodo q e che hanno immagine nell’insieme comprendente 0 e le radici φ(q)-esime dell’unità.
Dato un carattere di Dirichlet 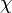 , si può definire il suo carattere coniugato
, si può definire il suo carattere coniugato  , definendolo semplicemente come
, definendolo semplicemente come

Chiaramente, se 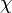 è un carattere di Dirichlet modulo q, anche
è un carattere di Dirichlet modulo q, anche  lo è. Un’altra importante proprietà dei caratteri di Dirichlet è la seguente:
lo è. Un’altra importante proprietà dei caratteri di Dirichlet è la seguente:
se χ è un carattere modulo q, allora per ogni coppia di interi m ed n con n e q coprimi si ha :

ove la somma è su tutti i caratteri modulo q .-
Osservazione 4
Il primo a notare l’importanza della funzione zeta di Riemann nello studio dei numeri primi fu Eulero che, nel 1737, dimostrò l’identità nota come prodotto di Eulero:

ove  è un numero reale maggiore di
è un numero reale maggiore di  . Grazie a questa formula, Eulero dedusse che la serie
. Grazie a questa formula, Eulero dedusse che la serie

diverge, e quindi che i numeri primi sono piuttosto densi nell’insieme dei numeri naturali, più dei quadrati perfetti, ad esempio (si può notare come il ragionamento di Eulero fornisca anche una diversa dimostrazione del teorema dell’infinità dei numeri primi, già elegantemente dimostrato dalla matematica greca).
Nel secolo seguente, Čebyšëv e altri matematici si dedicarono allo studio della comprensione della distribuzione dei numeri primi, utilizzando per lo più metodi di combinatoria e la formula prodotto di Eulero, senza tuttavia riuscire a dimostrare la relazione asintotica
-

Fu però con Bernhard Riemann che la funzione zeta di Riemann iniziò ad assumere un ruolo centrale nella teoria dei numeri. Nel suo unico articolo sull’argomento, Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse, Riemmann considerò la funzione zeta non più solo per una variabile reale  , ma per una variabile complessa
, ma per una variabile complessa  , e la studiò utilizzando metodi di analisi complessa. I risultati principali ottenuti da Riemann furono:
, e la studiò utilizzando metodi di analisi complessa. I risultati principali ottenuti da Riemann furono:
la dimostrazione del fatto che la funzione 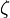 si possa prolungare analiticamente su tutto il piano complesso, ad eccezione di
si possa prolungare analiticamente su tutto il piano complesso, ad eccezione di  , in cui la funzione ha un polo semplice;
, in cui la funzione ha un polo semplice;
-
la scoperta di un’equazione funzionale (dimostrata in due diversi modi) che permette di mettere in relazione i valori della funzione zeta a destra e a sinistra della retta Re(s)=1/2;[3]
-
una formula esatta che mostra la dipendenza della funzione enumerativa dei primi dagli zeri della funzione zeta.
-
L’introduzione di una nuova funzione olomorfa intera, ξ(s), strettamente legata alla ζ(s), e un abbozzo di dimostrazione di una formula prodotto per ξ(s) (questa formula fu dimostrata rigorosamente solo 34 anni dopo, da Jacques Hadamard).
Oltre a questi risultati, Riemann diede alcune formule senza dimostrazione, tra cui una formula con una stima asintotica del numero di zeri non banali della funzione zeta, e scrisse che è “molto probabile” che tutti questi zeri abbiano parte reale uguale a 1/2. Questa congettura ha preso il nome di ipotesi di Riemann ed è tuttora uno dei problemi aperti più importanti di tutta la matematica, grazie alle conseguenze che implicherebbe sulla distribuzione dei numeri primi.
Negli anni a seguire, vari matematici svilupparono ulteriormente le idee di Riemann, e fornirono dimostrazioni rigorose per alcune sue formule. In particolare i risultati più importanti furono ottenuti da von Mangoldt e soprattutto da Hadamard e de la Vallée Poussin. Questi ultimi infatti riuscirono a dimostrare che la funzione zeta non ha zeri nella retta  e da questo ottenere come corollario il teorema dei numeri primi.
e da questo ottenere come corollario il teorema dei numeri primi.
Da allora, grossi sforzi sono stati fatti per dimostrare l’ipotesi di Riemann, ma sono stati ottenuti solo risultati parziali che restano molto lontani da quanto previsto da Riemann. Nell’impossibilità di fare ulteriori progressi in questa direzione, lo sforzo dei teorici dei numeri si è spostato su altri importanti problemi relativi alla funzione zeta: lo studio della crescita della funzione zeta lungo la retta critica, lo studio dei suoi momenti e sulla trascendenza o razionalità dei suoi valori sui numeri naturali dispari.
Osservazione 5
Proprietà principali.-
Il prodotto di Eulero
Una delle proprietà fondamentali della funzione zeta di Riemann, è il prodotto di Eulero,
-

valida per  , e dove il prodotto è effettuato su tutti i numeri primi
, e dove il prodotto è effettuato su tutti i numeri primi  . La dimostrazione di questa identità usa solo la formula per la somma della serie geometrica e il teorema fondamentale dell’aritmetica. Infatti, per
. La dimostrazione di questa identità usa solo la formula per la somma della serie geometrica e il teorema fondamentale dell’aritmetica. Infatti, per  , si può calcolare la somma geometrica
, si può calcolare la somma geometrica
-

per ogni primo  . Moltiplicando tra loro queste identità per tutti i primi
. Moltiplicando tra loro queste identità per tutti i primi  , per
, per  (questa ulteriore restrizione serve per assicurare la convergenza) si ha:
(questa ulteriore restrizione serve per assicurare la convergenza) si ha:
-

dato che per il teorema fondamentale dell’aritmetica ogni numero naturale si può decomporre in maniera unica come prodotto di potenze di primi.
È interessante notare che la formula di Eulero ha come conseguenza che vi sono infiniti numeri primi. Infatti, se vi fosse solo un numero finito di numeri primi allora il prodotto di Eulero sarebbe un prodotto finito e quindi sarebbe definito anche per 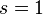 , mentre in tale punto la funzione zeta ha un polo. Sebbene possa sembrare esageratamente complicata per un teorema di cui esistono dimostrazioni elementari, questa dimostrazione è molto importante in quanto una sua generalizzazione è stata usata da Dirichlet per dimostrare il teorema dell’infinità dei numeri primi nelle progressioni aritmetiche.
, mentre in tale punto la funzione zeta ha un polo. Sebbene possa sembrare esageratamente complicata per un teorema di cui esistono dimostrazioni elementari, questa dimostrazione è molto importante in quanto una sua generalizzazione è stata usata da Dirichlet per dimostrare il teorema dell’infinità dei numeri primi nelle progressioni aritmetiche.
Questo prodotto è all’origine del collegamento tra funzione zeta e numeri primi.
Osservazione 6
La formula prodotto di Eulero o più semplicemente il prodotto di Eulero è una formula dimostrata da Leonhard Euler nel 1737.
-

dove 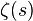 è la funzione zeta di Riemann e il prodotto del secondo membro dell’uguaglianza percorre tutti i numeri primi.
è la funzione zeta di Riemann e il prodotto del secondo membro dell’uguaglianza percorre tutti i numeri primi.
Questa formula è interessante in quanto mette in relazione una serie in cui compaiono tutti i numeri naturali e un prodotto in cui compaiono tutti i numeri primi. È all’origine del collegamento tra funzione zeta di Riemann e numeri primi che si presenta nell’ipotesi di Riemann
Prima Dimostrazione
Partiamo dalla funzione zeta:
-

se moltiplichiamo entrambi i termini per 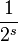 abbiamo che:
abbiamo che:
-
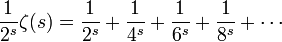
Sottraendo la seconda espressione dalla prima
-

In questa serie non compaiono denominatori pari.
Moltiplicando per il primo termine (dopo l’uno) rimasto
-

Sottraendo l’ultima alla penultima espressione, abbiamo che
-
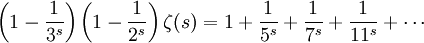
In questo procedimento abbiamo eliminato, prima tutti i multipli di due poi tutti i multipli del primo numero rimasto cioè tre, se poi lo facciamo di nuovo con cinque vedremo eliminati tutti i multipli di cinque:
-

Stiamo progressivamente eliminando tutti i multipli di ogni numero rimasto dopo l’uno (e che quindi è un numero primo visto che non è multiplo di nessun altro numero più piccolo). I numeri del prodotto prima dell’uguale quindi saranno tutti primi. Quindi ripetendo infinite volte il procedimento:
-

E in conclusione:
-
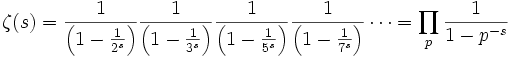
Seconda Dimostrazione
si può considerare il termine
-

come il numero a cui converge la serie geometrica
-

Quindi il prodotto di Eulero diviene:
-

E svolgendolo
-

-
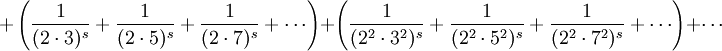
-
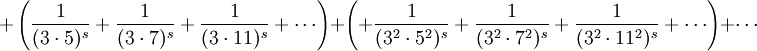
È chiaro che nel termine a destra dell’uguale appariranno prima o poi tutte le possibili combinazioni di numeri primi possibili (e a qualsiasi potenza). Per il teorema fondamentale dell’aritmetica abbiamo che queste combinazioni forniscono tutti i numeri naturali. Possiamo dunque riordinare i termini così:
-

Quindi:
-
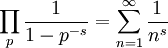
Osservazione 7
Infiniti numeri primi
Tramite questa formula Eulero diede una dimostrazione dell’infinità dei numeri primi. Infatti se si inserisce nella formula il numero 1 si ha:
-
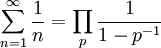
E siccome la somma nel primo membro è la serie armonica, che diverge, anche il prodotto deve farlo. Ma ciò è possibile solo se i suoi membri sono infiniti e quindi se esistono infiniti numeri primi.
Generalizzazione
Attraverso le dimostrazioni si può generalizzare questa formula per ogni funzione moltiplicativa a(x):
-

Dove P(p,s) è la serie:
-
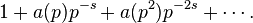
Osservazione 8
Esempi
Moltissime funzioni possono essere espresse con il prodotto di Eulero.
Queste funzioni danno origine a prodotti molto simili a quello sopra illustrato per la funzione zeta di Riemann.
Capita dunque di trovare collegamenti tra queste serie di funzioni e la funzione zeta.
Ad esempio:
-

-
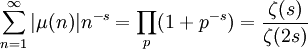
-

E altri che utilizzano la funzione zeta come:
-

Dove  è il numero di fattori primi distinti di n
è il numero di fattori primi distinti di n
E anche
-

dove σ(n) è la somma di tutti i divisori di n (1 e n compresi).
Teoria dei numeri
Il logaritmo integrale ha un ruolo molto importante nella teoria dei numeri; infatti, il teorema dei numeri primi afferma che:

dove  è la funzione enumerativa dei primi, ovvero la funzione che indica il numero di numeri primi minori di
è la funzione enumerativa dei primi, ovvero la funzione che indica il numero di numeri primi minori di  . In pratica la formula può essere usata per avere una buona approssimazione del numero di primi inferiori o uguali a
. In pratica la formula può essere usata per avere una buona approssimazione del numero di primi inferiori o uguali a  . Il valore di
. Il valore di  rimane superiore a
rimane superiore a  fino a numeri estremamente grandi, tanto che molti matematici pensavano che dovesse rimanere sempre superiore. Nel 1914 però Littlewood dimostrò che la differenza
fino a numeri estremamente grandi, tanto che molti matematici pensavano che dovesse rimanere sempre superiore. Nel 1914 però Littlewood dimostrò che la differenza  , pur rimanendo positiva fino a numeri estremamente grandi, in seguito cambia di segno infinite volte, per cui esistono infiniti valori di
, pur rimanendo positiva fino a numeri estremamente grandi, in seguito cambia di segno infinite volte, per cui esistono infiniti valori di  per i quali
per i quali  è maggiore di
è maggiore di 
Nel 1933 il matematico sudafricano Stanley Skewes dimostrò un limite superiore per il più piccolo di tali valori. Assumendo che l’ipotesi di Riemann sia vera, egli valutò tale limite in circa  . In seguito questo limite, immensamente grande, è stato notevolmente abbassato, e attualmente è di 1,39×10316 (C. Bay & R.H. Hudson, 2000).[1]
. In seguito questo limite, immensamente grande, è stato notevolmente abbassato, e attualmente è di 1,39×10316 (C. Bay & R.H. Hudson, 2000).[1]
Sviluppo asintotico
Il comportamento asintotico per  è:
è:

dove  è la notazione O-grande. L’espansione completa ha la forma:
è la notazione O-grande. L’espansione completa ha la forma:

o equivalentemente:

Si tratta di una serie divergente, che rappresenta una buona approssimazione solo se viene troncata, ed è utilizzata per grandi valori di  Segue direttamente dall’espansione dell’integrale esponenziale.
Segue direttamente dall’espansione dell’integrale esponenziale.
°°°°°
Read the rest of this entry »

























![{\ displaystyle {\ frac {1} {2T)) \ int _ {- T} ^ {T} dt | F (a + it) | ^ {2} dt = \ sum _ {n = 1} ^ {\ infty} [f (n)] ^ {2} n ^ {- 2a} {\ text {per)) T \ sim \ infty.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ea3980c0bc33096504d857d0a6648cc8b584aa4)










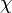 , si può definire il suo carattere
, si può definire il suo carattere  , definendolo semplicemente come
, definendolo semplicemente come


 è un
è un  . Grazie a questa formula, Eulero dedusse che la serie
. Grazie a questa formula, Eulero dedusse che la serie

 , e la studiò utilizzando metodi di
, e la studiò utilizzando metodi di 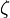 si possa
si possa  e da questo ottenere come corollario il
e da questo ottenere come corollario il 
 , e dove il
, e dove il  . La dimostrazione di questa identità usa solo la formula per la somma della
. La dimostrazione di questa identità usa solo la formula per la somma della  , si può calcolare la somma geometrica
, si può calcolare la somma geometrica

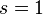 , mentre in tale punto la funzione zeta ha un polo. Sebbene possa sembrare esageratamente complicata per un teorema di cui esistono dimostrazioni elementari, questa dimostrazione è molto importante in quanto una sua generalizzazione è stata usata da
, mentre in tale punto la funzione zeta ha un polo. Sebbene possa sembrare esageratamente complicata per un teorema di cui esistono dimostrazioni elementari, questa dimostrazione è molto importante in quanto una sua generalizzazione è stata usata da 
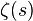 è la
è la 
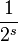 abbiamo che:
abbiamo che: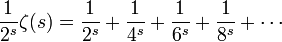


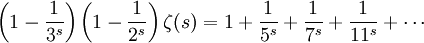


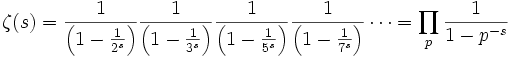




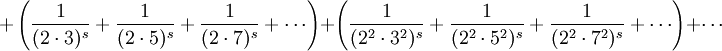
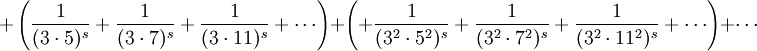

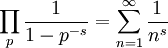
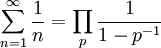

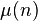 :
:
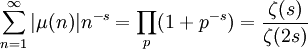


 è il numero di
è il numero di 

























Devi effettuare l'accesso per postare un commento.