Topologia

°°°°°

°°°°°

Topologia

La topologia (dal greco τόπος, tópos, “luogo”, e λόγος, lógos, “studio”, col significato quindi di “studio dei luoghi'”) è una branca della geometria che studia le proprietà delle figure, e in generale degli oggetti matematici, che non cambiano quando viene effettuata una deformazione senza “strappi”, “sovrapposizioni” o “incollature”.

È una delle più importanti branche della matematica moderna.

Concetti fondamentali come

convergenza, 

limite, 

continuità, 

connessione  

compattezza 

trovano nella topologia la loro migliore formalizzazione.

Si basa essenzialmente sui concetti di:

spazio topologico,

funzione continua

omeomorfismo.

Col termine

topologia si indica anche la collezione di aperti che definisce uno spazio topologico.

Per esempio

un cubo e una sfera sono oggetti topologicamente equivalenti (cioè omeomorfi),

perché possono essere deformati l’uno nell’altro senza ricorrere ad alcuna incollatura, strappo o sovrapposizione;

una sfera e un toro non sono oggetti topologicamente equivalenti,

perché il toro contiene un “buco” che non può essere eliminato da una deformazione.

Storia

I sette ponti di Königsberg, uno dei primi problemi topologici

L’antenata della topologia è la geometria antica.

L’articolo di Eulero del 1736 sui Sette ponti di Königsberg è visto come uno dei primi risultati che non dipendono da alcun tipo di misura, vale a dire uno dei primi risultati topologici.

Georg Cantor,

l’inventore della teoria degli insiemi, iniziò a studiare la teoria degli insiemi di punti nello spazio euclideo verso la fine del XIX secolo.

Nel 1895, nel suo Analysis Situs ,

Henri Poincaré 

introdusse i concetti di omotopia e omologia, adesso considerati parte della topologia algebrica.

A metà ‘800 risale la corrispondenza fra i matematici italiani

Enrico Betti 

Placido Tardy,

raccolta a cura di André Weil, che verteva in particolare sulla connessione degli spazi topologici.

Maurice Fréchet,

unificando il lavoro sugli spazi di funzioni di Cantor,

Vito Volterra,

Arzelà, 

Hadamard,

Ascoli 

e altri,

nel 1906 introdusse il concetto di

spazio metrico.

Nel 1914

Felix Hausdorff,

generalizzando la nozione di spazio metrico, coniò il termine di spazio topologico e definì quello che oggi è detto

spazio di Hausdorff.

Finalmente,

nel 1922 Kuratowski, con un’ulteriore lieve generalizzazione, fornì il concetto odierno di

spazio topologico.

°°°°°

Introduzione elementare

Gli spazi topologici sono usati quotidianamente dall’analisi matematica, dall’algebra astratta, dalla geometria: questo rende la topologia una delle grandi idee unificanti della matematica.

La topologia generale 

(o topologia degli insiemi di punti) definisce e studia alcune proprietà utili degli spazi e delle mappe, come la loro connessione, la compattezza e la continuità.

La topologia algebrica 

è un potente strumento per studiare gli spazi topologici e le mappe fra essi: essa assegna loro invarianti “discreti” (ad esempio numeri, gruppi, o anelli), più calcolabili, spesso servendosi di funtori.

Le idee della topologia algebrica hanno avuto una grande influenza sull’algebra e sulla geometria algebrica.

Se tre insiemi chiusi ricoprono una sfera, almeno uno di questi contiene due punti antipodali:

questo fatto può essere dimostrato con strumenti topologici.

°°°°°

Un enunciato analogo è fornito dal

teorema di Borsuk-Ulam:

esistono sempre due punti antipodali sulla Terra aventi la stessa temperatura e la stessa pressione atmosferica.

La motivazione profonda della topologia è che alcuni problemi geometrici non dipendono dalla forma esatta degli oggetti coinvolti, ma piuttosto “dal modo in cui questi sono connessi”.

Per esempio

il teorema della sfera pelosa

della topologia algebrica dice che

“non si può pettinare in modo continuo il pelo di una sfera pelosa”.

Questo fatto è evidente per molte persone, anche se probabilmente non lo riconoscerebbero leggendo l’enunciato formale del teorema, e cioè che non esiste un campo vettoriale continuo e non nullo di vettori tangenti alla sfera stessa.

Come per i Ponti di Königsberg, il risultato non dipende dall’esatta forma della sfera, ma si applica anche a forme sferiche non regolari e in generale ad ogni tipo di oggetto (purché la sua superficie soddisfi certi requisiti di continuità e regolarità) che non abbia buchi.

Per trattare problemi che non considerano la forma esatta degli oggetti, bisogna mettere bene in chiaro quali sono le proprietà degli oggetti su cui possiamo contare:

da questo bisogno nasce la nozione di

equivalenza topologica.

L’impossibilità di attraversare ogni ponte una e una sola volta è vera per ogni configurazione di ponti topologicamente equivalente a quelli di Königsberg,

e

il problema della sfera pelosa si applica ad ogni spazio topologicamente equivalente a una sfera.

Formalmente,

due spazi sono topologicamente equivalenti se esiste un omeomorfismo fra loro:

in questo caso sono detti omeomorfi e sono,

ai fini topologici, esattamente identici.

Una deformazione continua di una tazza di caffè in un toro.

Le deformazioni continue vengono formalizzate nelle nozioni di omeomorfismo e omotopia.

Un omeomorfismo è formalmente definito come una funzione biettiva continua dotata di una inversa continua,

il che non è molto intuitivo anche per chi conosce già il significato delle parole nella definizione.

Una definizione meno formale restituisce meglio il senso di quanto sopra:

due spazi sono topologicamente equivalenti se è possibile trasformare l’uno nell’altro senza tagliare né incollare insieme pezzi dei due.

Ad esempio,

una tazza e una ciambella sono omeomorfi, come suggerito dall’animazione qui accanto.

Un semplice esercizio introduttivo consiste nel classificare le lettere maiuscole dell’alfabeto per classi di equivalenza topologica.

Si ottiene il risultato seguente:

Esiste una nozione di equivalenza più debole dell’omeomorfismo, detta omotopia.

Informalmente, questa nozione permette di trasformare gli oggetti l’uno nell’altro in modo leggermente più libero: è possibile ad esempio trasformare una Q in una O accorciando progressivamente il piede della lettera Q fino a farlo scomparire.

Si ottengono le classi seguenti:

Quest’ultima nozione distingue le lettere essenzialmente per il numero di “buchi”: {A,R,D,O,P,Q} ne hanno uno, {B} ne ha due, tutte le altre lettere nessuno.

Il numero di buchi è quindi un invariante, una quantità utile a distinguere oggetti.

Tale quantità si realizza formalmente con il concetto di gruppo fondamentale.

Due ladri si spartiscono una collana rubata, con perle di due tipi diversi:

esiste sempre un modo di tagliare la collana in due pezzi, contenenti lo stesso numero di palline dei due tipi.

La topologia si presta molto bene anche per un approccio elementare allo studio della geometria.

Il già citato “problema dei 7 ponti”, ad esempio porta a riflessioni sulle reti nel piano, con nodi, archi e superfici.

Il “problema dei 4 colori” affronta il tema di come si può colorare col minor numero possibile di colori diversi una superficie divisa in regioni separate, come potrebbe essere la cartina dell’Italia politica.

Lo stesso nastro di Möbius costruito con carta, con la sua unica faccia ed il suo unico bordo, tagliato longitudinalmente in vari modi, consente osservazioni interessanti che stupiscono quasi come giochi di prestigio.

°°°°°

Nozioni di base

La nozione fondamentale in topologia è quella di

spazio topologico.

Uno spazio topologico è un insieme  di punti, dotato di una struttura che realizzi i concetti di vicinanza e lontananza fra questi.

La struttura consiste in una collezione di insiemi di , detti aperti, che soddisfano delle proprietà simili a quelle degli insiemi aperti della retta reale .

Spazio topologico

Uno spazio topologico è un insieme  di punti su cui sono definiti dei particolari sottoinsiemi, detti aperti.

Questi sottoinsiemi devono però soddisfare alcune proprietà.

Qui sono mostrate

sei scelte diverse per l’insieme di tre punti solo le prime quattro danno veramente luogo ad uno spazio topologico (nella quinta manca l’unione di {2} e {3}, nella sesta manca l’intersezione di {1,2} e {2,3}).

Si definisce 

topologia 

una collezione  di sottoinsiemi di un insieme  tali che:

• L’insieme vuoto e  appartengono a  :   e 

• L’unione di una quantità arbitraria di insiemi appartenenti a  appartiene a  : 

• L’intersezione di due insiemi appartenenti a  appartiene a  : 

Uno spazio topologico è una coppia (, ),

dove

  è un insieme

e

  una topologia.

In uno spazio topologico

gli insiemi che costituiscono T si dicono aperti in .

I complementari degli insiemi aperti sono detti chiusi,

sempre in analogia con gli insiemi chiusi di 

Inoltre dalla terza condizione di topologia, e per induzione, si deduce che

l’intersezione di un numero finito di insiemi appartenenti a  appartiene a .

°°°°°

Uno spazio metrico è un particolare spazio topologico,

in cui due punti  hanno una definita distanza che quantifica concretamente la vicinanza (o lontananza) fra i due punti.

È importante sottolineare però che la nozione di spazio topologico è più generale e flessibile, perché non necessita di definire con precisione la distanza fra due punti.

Lo spazio euclideo  di dimensione  è uno spazio metrico e quindi topologico.

In particolare,

il piano cartesiano

lo spazio 3-dimensionale

sono

spazi topologici.

Ogni sottoinsieme di uno spazio topologico è anch’esso in modo naturale uno spazio topologico.

Ne segue che qualsiasi oggetto contenuto nel piano o nello spazio è uno spazio topologico:

ad esempio

un poligono,

una corona circolare

o

oggetti molto più complessi come

i frattali

sono spazi topologici contenuti nel piano;

una tazza,

una ciambella,

un nastro di Möbius

sono spazi topologici contenuti nello spazio.

Molti spazi topologici non sono contenuti né nel piano né nello spazio:

un esempio

è la bottiglia di Klein (che è però contenuta nello spazio 4-dimensionale).

°°°°°

Funzioni continue

La nozione di funzione continua è utile a modellizzare in modo rigoroso le “deformazioni ammissibili” che

ad esempio trasformano una tazza in una ciambella.

Una funzione

fra due spazi topologici è continua 

se

la controimmagine di un insieme aperto di  è un insieme aperto di .

Questa nozione usa l’unica struttura a disposizione (gli insiemi aperti) e per quanto espressa in modo totalmente differente coincide (per funzioni da  in ) con la più usuale nozione di funzione continua definita in analisi matematica con l’ausilio del calcolo infinitesimale, ovvero degli  e dei .

Due spazi topologici  e  sono quindi omeomorfi se esistono due funzioni continue

che sono una l’inversa dell’altra.

In altre parole,

esiste una corrispondenza biunivoca fra  e  che mette in corrispondenza gli insiemi aperti di  con

gli insiemi aperti di  

Due spazi topologici omeomorfi sono quindi in un certo senso “uguali”

(da un punto di vista topologico).

Ad esempio,

tazza e ciambella sono omeomorfi.

Quadrato e cerchio sono omeomorfi.

Ovviamente tali spazi possono non essere “uguali” se considerati da altri punti di vista:

come spazi metrici, il quadrato ed il cerchio non sono uguali.

°°°°°

Spazio connesso

Lo spazio A è connesso, lo spazio B no (ha 4 componenti connesse).

 

Questo spazio è connesso per archi: qualsiasi coppia di punti può essere collegata da un arco continuo.

Uno spazio topologico  è connesso se è “fatto di un pezzo solo”.

Formalmente,

si chiede che  non sia l’unione di due aperti disgiunti (entrambi non vuoti).

Una nozione lievemente più forte è quella di

connessione per archi:

  è connesso per archi se ogni coppia di punti è collegata da un arco continuo.

Uno spazio topologico è sempre unione disgiunta di alcuni spazi connessi naturali, detti componenti connesse.

°°°°°

Spazio compatto

In topologia la nozione di compattezza ha un ruolo molto importante.

Uno spazio topologico  contenuto in  è compatto se è chiuso e limitato:

ad esempio,

la ciambella è compatta,

mentre una retta no (perché è illimitata);

una palla che contiene anche il suo bordo è compatta,

una palla senza bordo no (perché non è chiusa).

La nozione di compattezza è definita per uno spazio arbitrario  nel modo seguente:

  è compatto se ogni ricoprimento aperto contiene un sottoricoprimento finito.

Per spazi metrici,

questa nozione equivale alla definizione seguente usata in analisi:

uno spazio è compatto se ogni successione ammette una sottosuccessione convergente.

Informalmente,

uno spazio è compatto se qualsiasi successione di punti converge (in un certo senso…) a qualcosa.

L’ipotesi di connessione per uno spazio topologico  non è molto forte:

se  non è connesso,

si può comunque spezzare nelle sue componenti connesse e questo in molti contesti non causa grossi problemi.

L’ipotesi di compattezza è però più forte:

molti risultati (come il teorema di Weierstrass) sono validi solo per spazi compatti, e non si estendono facilmente a spazi non compatti.

°°°°°

Assiomi di separazione e numerabilità

Nella sua definizione del 1914,

Felix Hausdorff chiede che uno spazio topologico soddisfi questo ulteriore assioma, oggi detto T2:

per ogni coppia di punti  dello spazio esistono due aperti disgiunti  che li contengono rispettivamente.

Questo assioma è soddisfatto da molti spazi topologici

(ad esempio tutti gli spazi metrici),

ma non da tutti

(ad esempio dalla topologia di Zariski usata in geometria algebrica).

La definizione di spazio topologico è molto generale e prevede anche la trattazione di oggetti molto lontani dalla nostra comune intuizione data dallo spazio tridimensionale in cui viviamo.

Per evitare spazi topologici troppo “esotici” si mettono in alcuni casi nella definizione degli assiomi aggiuntivi.

°°°°°

Gli assiomi più usati sono di due tipi.

Gli assiomi di separazione 

riguardano il modo in cui i punti o i chiusi di uno spazio vengono “separati” dalla topologia.

La nomenclatura standard codifica questi assiomi con i simboli T0, T1, T2, T3 e T4 (e altre varianti).

Tra questi l’assioma più usato è T2, detto anche di Hausdorff perché incluso da Felix Hausdorff nel 1914 nella sua definizione di spazio topologico.

Gli assiomi di numerabilità

richiedono che lo spazio topologico non sia “troppo grosso”.

Questi assiomi non assumono che lo spazio sia numerabile, perché sarebbe una condizione troppo forte, visto che taglierebbe fuori dalla teoria lo spazio euclideo  che ha la cardinalità del continuo.

Richiedono però che un insieme numerabile di aperti sia sufficiente per determinare tutta la topologia dello spazio.

°°°°°

Varietà topologica

La circonferenza è una varietà topologica di dimensione 1: ogni punto ha un intorno omeomorfo ad un intervallo aperto di .

Una varietà topologica di dimensione  è uno spazio topologico in cui ogni punto ha un intorno omeomorfo ad un insieme aperto di .

La nozione di varietà è molto importante nella geometria contemporanea, perché è l’oggetto base usato per definire la nozione di “spazio curvo di dimensione arbitraria” utile ad esempio per modellizzare l’universo secondo la relatività generale.

Questa superficie, considerata vuota all’interno come se fosse un palloncino, è una varietà di dimensione 2.

Ad esempio,

con  e 

si ottengono curve

(come la circonferenza)

e

superfici

(come la sfera, il toro, ed altre superfici più esotiche quali il nastro di Möbius, la bottiglia di Klein, …)

Le varietà di dimensione 3, dette 3-varietà, sono più difficili da visualizzare.

Tra queste troviamo l’ipersfera.

°°°°°

Applicazioni

Teoria dei grafi

Il problema dei sette ponti di Königsberg, tradotto nel linguaggio della teoria dei grafi, chiede se esista un circuito euleriano, ovvero un percorso chiuso che passa attraverso tutti gli spigoli una volta sola.

Un grafo è un oggetto formato da vertici (o nodi) collegati da segmenti detti spigoli.

Gli spigoli non sono dotati di lunghezza o di curvatura:

l’unico dato utile di ciascuno spigolo è la coppia di vertici che collega.

Un grafo può essere descritto in modo pressoché equivalente usando il linguaggio della combinatoria o della topologia.

Il problema dei ponti di Königsberg,

considerato storicamente uno dei primi problemi topologici, è un classico problema della teoria dei grafi.

Nello stesso ambito,

il teorema dei quattro colori 

è un importante teorema modellizzato e recentemente dimostrato usando i grafi.

In topologia,

un grafo è uno spazio topologico relativamente semplice.

Il gruppo fondamentale o l’omologia misurano il numero di cicli (“buchi”) del grafo.

Esiste una nozione di dimensione topologica, secondo la quale i grafi hanno dimensione 1.

Oggetti di dimensione superiore che generalizzano i grafi sono i complessi di celle (o simpliciali).

°°°°°

Calcolo differenziale

Nel calcolo differenziale e integrale viene studiato spesso un insieme aperto  di , che può essere ad esempio il dominio di una funzione, di un campo vettoriale o di una forma differenziale.

La topologia di  fornisce molte informazioni sull’esistenza e proprietà di tali oggetti:

ad esempio,

se  “non ha buchi” allora ogni forma differenziale chiusa è in realtà esatta;

la nozione appropriata di “buco” non è però banale in questo contesto, ed è rigorosamente codificata dalla omologia

(in questo contesto, dalla coomologia di De Rham).

Il calcolo differenziale è anche usato per studiare altri oggetti, come le superfici in .

La topologia di tali superfici fornisce anche qui delle importanti informazioni.

Ad esempio,

un campo vettoriale tangente mai nullo su una superficie chiusa nello spazio esiste se e solo se si annulla un importante invariante topologico della superficie, la caratteristica di Eulero.

In particolare, non esiste un tale campo sulla sfera, mentre esiste sul toro (questo risultato è noto anche come il teorema della sfera pelosa).

In analisi complessa 

si fa spesso uso di funzioni meromorfe,

definite su un aperto  ottenuto rimuovendo alcuni punti dal piano complesso .

Lo studio di tali funzioni e di nozioni come residuo, polo, integrale di linea, ecc. sono strettamente connesse alla nozione topologica di gruppo fondamentale di .

°°°°°

Analisi funzionale

La successione di funzioni mostrata in figura converge, in un opportuno spazio vettoriale topologico, a una particolare “funzione” che vale infinito in zero e zero negli altri punti.

Questa “funzione”, detta delta di Dirac, non è in realtà una funzione ma un oggetto più generale, chiamato distribuzione.

L’analisi funzionale è la branca dell’analisi che studia gli spazi di funzioni, generalmente con lo scopo di risolvere una equazione differenziale, cioè di trovare una particolare funzione le cui derivate soddisfano delle determinate proprietà.

Lo spazio di funzioni considerato è generalmente uno spazio vettoriale topologico di dimensione infinita.

La topologia gioca qui un ruolo importante:

sullo stesso spazio di funzioni esistono spesso varie topologie diverse, e la scelta di quella più adatta al problema in esame è un aspetto cruciale della teoria.

Alcune topologie sono indotte da una norma completa:

in questo caso si ottengono degli

spazi di Banach

spazi di Hilbert,

come

gli spazi Lp

spazi di Sobolev.

In altri casi si usa una topologia più debole, ad esempio con le distribuzioni.

°°°°°

Geometrie non euclidee

Una geometria non euclidea è

una geometria che soddisfa i primi 4 postulati di Euclide, ma non il quinto.

L’esistenza di tali geometrie è stata mostrata inizialmente nel XIX secolo; successivamente, la stessa nozione di “geometria” è stata ridiscussa numerose volte.

Oggi una nozione che descrive efficacemente e in modo molto generale una “geometria” è quella di

varietà riemanniana,

ovvero un oggetto topologico (una varietà) dotato di opportune strutture ereditate dal

calcolo infinitesimale che permettano di definire le nozioni di retta (più precisamente, geodetica), angolo, volume, ecc.

In questo contesto,

la geometria euclidea è la geometria del piano

(e più in generale dello spazio euclideo di dimensione ),

che può essere caratterizzata come l’unica varietà semplicemente connessa avente curvatura nulla.

Altre geometrie fondamentali sono

la geometria sferica

la geometria iperbolica,

aventi curvatura sezionale costante positiva e negativa.

°°°°°

Geometria algebrica

La topologia di Zariski sul piano  è diversa da quella usuale. Si dice che è meno fine, perché contiene meno aperti (e quindi anche meno chiusi!).

Gli insiemi chiusi di questa topologia sono solo le varietà affini,

ovvero

gli insiemi che sono zeri di polinomi in due variabili:

qui sono mostrati

ad esempio

due circonferenze,

una parabola,

un’iperbole,

una cubica (definita da un’equazione di terzo grado).

La geometria algebrica è un’importante branca della matematica che unisce l’algebra alla geometria.

Oggetto principale di studio sono le varietà algebriche, ovvero i luoghi di punti che sono zeri di alcuni polinomi a coefficienti in un campo , che può essere ad esempio il campo dei numeri reali  o dei numeri complessi .

°°°°°

In questo contesto è utile definire una topologia particolare, detta

topologia di Zariski,

in cui gli insiemi chiusi sono forniti proprio dalle varietà algebriche

(e gli aperti sono i loro complementari).

Questa topologia è molto lontana dall’usuale topologia euclidea:

aperti e chiusi sono in quantità minore e conseguentemente lo spazio non è di Hausdorff.

La nozione di varietà algebrica è stata quindi estesa a quella più astratta e intrinseca di schema:

anch’esso è un particolare spazio topologico con delle strutture algebriche aggiuntive.

°°°°°

Relatività generale

La relatività generale di Einstein 

modellizza l’intero spaziotempo come uno “spazio curvo di dimensione 4”.

Lo spazio di dimensione 4 è definito topologicamente come una varietà 4-dimensionale; la sua curvatura dipende in ogni punto dalla massa/energia (secondo l’equazione di campo di Einstein) ed è codificata tramite una struttura aggiuntiva abbastanza complessa (il tensore di Riemann) propria della geometria differenziale.

L’oggetto risultante è una

varietà pseudoriemanniana.

°°°°°

Strumenti

Tagliare e incollare

Una delle idee cardine della teoria consiste nel fatto che uno spazio topologico non muta se deformato senza strappi.

Strappi e ricuciture possono in effetti variare drasticamente la topologia di uno spazio:

queste operazioni di “sartoria” sono comunque utili in molte occasioni, perché permettono di creare nuovi spazi topologici a partire da spazi dati.

Si può ottenere un toro partendo da un quadrato, incollando prima i lati opposti di tipo A e quindi i lati opposti di tipo B (l’ordine in cui vengono incollati non è importante).

Se i lati opposti di tipo A sono incollati con orientazione invertita, la superficie che si ottiene è invece

una bottiglia di Klein.

Ad esempio,

un oggetto complesso come il toro può essere ottenuto da un oggetto più semplice, il quadrato, incollando i lati opposti come suggerito in figura.

Incollando i lati in modo lievemente diverso si ottiene una superficie ben più complessa, la bottiglia di Klein.

Molte delle proprietà di questi oggetti complessi possono essere studiate direttamente sul quadrato, tenendo bene a mente le identificazioni (codificate dalle frecce di colore diverso).

L’operazione di incollamento è un’operazione molto generale, che permette di costruire

uno spazio topologico quoziente a partire da qualsiasi relazione di equivalenza fra punti.

Compattificazioni

La proiezione stereografica mostra come ottenere una sfera (compatta) da un piano (non compatto) aggiungendo un “punto all’infinito”.

Questa operazione può essere effettuata su qualsiasi spazio topologico e si chiama

compattificazione di Alexandroff.

In molti contesti è utile aggiungere ad uno spazio topologico i suoi “punti all’infinito”.

Spesso questa operazione trasforma uno spazio non compatto in uno compatto, ed è quindi detta compattificazione.

Una compattificazione può però essere fatta in vari modi diversi.

Ad esempio,

alla retta reale  si possono aggiungere i due infiniti  e  ed ottenere la retta estesa

Topologicamente la retta reale è omeomorfa all’intervallo aperto ,

e quindi

la retta estesa è omeomorfa all’intervallo chiuso .

Alternativamente,

si può aggiungere a  un infinito solo e

ottenere che è omeomorfo alla circonferenza tramite proiezione stereografica.

La compattificazione che aggiunge un punto solo è

la compattificazione di Alexandroff.

Un’altra compattificazione, che aggiunge generalmente molti più punti, è

la compattificazione di Stone-Čech.

La proiezione stereografica mostra che la compattificazione di Alexandroff dello spazio euclideo  è un’ipersfera 

Un’altra compattificazione molto importante di  è

lo spazio proiettivo, che aggiunge un punto per ogni “direzione all’infinito”.

Gruppo fondamentale

Il gruppo fondamentale dello spazio ottenuto rimuovendo un punto dal piano è isomorfo a . La curva che fa due giri mostrata in figura corrisponde al valore intero “2”.

Il gruppo fondamentale di un toro è : i due generatori  e , corrispondenti a  e , sono mostrati in figura. La scelta del punto base  è ininfluente perché il toro è connesso.

Il gruppo fondamentale di uno spazio topologico  è un oggetto algebrico (un gruppo) che codifica in modo efficiente i “buchi” presenti in .

Tale gruppo è definito fissando un punto di  (detto punto base) e considerando tutti i cammini continui che partono dal punto base, si muovono in  e quindi tornano nel punto base.

Questi cammini sono considerati a meno di spostamenti continui (cioè omotopie) e possono essere concatenati; con questa operazione di concatenamento, i cammini formano effettivamente un gruppo.

Uno spazio connesso avente gruppo fondamentale banale è detto semplicemente connesso.

Sono semplicemente connessi

 ,

la sfera  con ,

il disco .

In uno spazio semplicemente connesso ogni cammino chiuso può essere strizzato ad un punto (sempre tramite omotopia).

La nozione di gruppo fondamentale, associata a quella di rivestimento, è uno strumento fondamentale in topologia.

Omologia

La sfera (vuota al suo interno) ha solo un “buco 2-dimensionale”. Infatti il gruppo fondamentale (che misura i buchi 1-dimensionali) è banale, ma il secondo gruppo di omologia  è .

I gruppi di omologia di uno spazio topologico  sono dei gruppi abeliani che similmente al gruppo fondamentale codificano i “buchi” dello spazio topologico .

In un certo senso, il gruppo fondamentale fa uso dei cammini, che sono oggetti 1-dimensionali, e quindi codifica solo i “buchi 1-dimensionali”.

I gruppi di omologia usano anche oggetti di dimensione superiore e quindi codificano i “buchi -dimensionali” per ogni  ecc.

Per ciascun  è quindi definito un gruppo di omologia .

Ad esempio,

la sfera  ha un “buco -dimensionale” al suo interno.

Il gruppo fondamentale si accorge di questo buco soltanto per la circonferenza, cioè per :

in questo caso il gruppo fondamentale è , mentre per ogni  è banale.

L’omologia però si accorge dell’esistenza di questo buco per ogni valore di :

infatti è sempre .

Nel caso 1-dimensionale, il gruppo fondamentale è però uno strumento più raffinato (e generalmente più utile) del gruppo di omologia ; in effetti,  è isomorfo alla versione abelianizzata del gruppo fondamentale di  (teorema di Hurewicz).

Omotopia

Un piano tangente al punto di una sfera. La nozione di piano tangente a una superficie è definita solo se questa ha una struttura differenziabile.

Un’omotopia è una deformazione continua fra oggetti, o più generalmente fra funzioni.

Applicata ai cammini continui, permette di definire il gruppo fondamentale di uno spazio topologico e di studiarne molte proprietà.

Applicata agli spazi topologici, permette di trasformare uno spazio topologico in un altro con più libertà di quanto offerto dalla più rigida nozione di omeomorfismo.

Ad esempio,

permette di “contrarre” alcune parti dello spazio topologico trasformandole (con continuità!) ad un punto.

Ad esempio,

un disco, un segmento e un punto sono tutti omotopicamente equivalenti, anche se non sono omeomorfi.

Le relazioni fra le due nozioni di omotopia e omeomorfismo sono spesso non banali.

Ad esempio,

la congettura di Poincaré,

formulata nel 1904 e dimostrata solo nel 2003,

asserisce che

una varietà topologica di dimensione 3, omotopicamente equivalente all’ipersfera , è in realtà omeomorfa a questa.

Omotopia e logica classica

L’introduzione del libro Homotopy Type Theory: Univalent Foundations of Mathematics, per la prima volta pubblicato nel 2013, afferma che

introducendo l’assioma della scelta

e

dell’assioma del terzo escluso nella teoria dei tipi omotopici,

è possibile costruire un continuo degli n-tipi possibili , del quale la logica classica e la logica costruttivista sono rispettivamente l’estremo inferiore e superiore (p. 9).

Esiste una tabella di equivalenza fra i tipi e gli operatori definibili nelle teorie logica, topologica, omotopici (p. 11). Vale quanto segue:

• in numerosi sistemi è vantaggioso applicare un sottoinsieme di tipi per cui valgono gli assiomi della scelta e del terzo escluso, lasciando i restanti nel campo della generale logica costruttivista;

• la teoria del tipi omotopici fornisce solidi motivi per limitare l’uso dei principi della logica classica ai soli casi effettivamente necessari.

  °°°°°

Struttura differenziabile

Nella moltitudine di spazi topologici esistenti, le varietà giocano un ruolo centrale.

Una varietà di dimensione  è un oggetto in cui ogni punto ha un intorno aperto omeomorfo a .

Esempi classici sono le superfici in , come la sfera o il toro. In queste superfici, un piccolo intorno di un punto è come un disco bidimensionale, però leggermente incurvato.

La nozione di curvatura non è però una nozione topologica.

Per poter dare un senso a domande del tipo “quanto è curva la superficie?”, “esiste un campo vettoriale tangente?”, “cosa è la derivata (più precisamente, il differenziale) di una funzione fra due varietà?” è necessario attrezzare le varietà topologiche di alcune strutture aggiuntive, che fanno uso del calcolo infinitesimale.

Senza queste strutture aggiuntive queste domande non hanno senso.

Una varietà dotata di una struttura aggiuntiva di questo tipo è una varietà differenziabile.

In una varietà differenziabile sono definite le nozioni di vettore tangente, di funzione differenziabile, ecc.

Per definire una nozione di curvatura è però necessaria un’ulteriore (e ben più complicata) struttura, quella di varietà riemanniana.

°°°°°

Teoremi

Sulla compattezza

Teorema di Heine-Borel

Un sottoinsieme di  è compatto se e solo se è chiuso e limitato.

Sono quindi compatti i poligoni, i poliedri, una ellisse, un ellissoide.

Non sono compatti rette, piani e gli altri sottospazi affini (perché non limitati), né una palla aperta (perché non chiusa).

Il teorema non si estende però a spazi vettoriali topologici arbitrari di dimensione infinita, come gli spazi Lp.

Teorema di Weierstrass

Una funzione reale continua definita sull’intervallo chiuso  ha sempre un punto di massimo e uno di minimo. Questo teorema può essere esteso ad ogni funzione continua fra spazi topologici nel modo seguente: l’immagine di un compatto è sempre compatta.

Il teorema di Weierstrass è un risultato classico di analisi matematica che ha una naturale generalizzazione in topologia.

Il teorema asserisce che ogni funzione continua

ammette un massimo ed un minimo.

Da un punto di vista topologico, questo è conseguenza di un fatto più generale:

per ogni funzione continua

fra spazi topologici, se il dominio  è compatto allora anche l’immagine  è compatta.

Informalmente, una funzione continua manda compatti in compatti.

Nel caso in cui il codominio  sia , l’immagine  è un compatto in , e per il teorema di Heine-Borel è un chiuso e limitato.

L’insieme  ha quindi un massimo e un minimo.

Quindi una funzione continua a valori reali definita su un qualsiasi spazio compatto ha sempre punti di massimo e minimo.

Teorema di Tychonoff

Il teorema di Tychonoff assicura che il prodotto di due o più spazi topologici compatti è compatto.

Ad esempio,

il prodotto di due circonferenze  è compatto (si tratta in realtà di un toro).

Il teorema di Tychonoff è valido per un prodotto avente una quantità arbitraria (anche infinita) di fattori.

Sulle funzioni continue

Teorema del punto fisso di Brouwer

Una conseguenza del teorema del punto fisso di Brouwer: non è possibile estendere questo campo vettoriale all’interno del disco senza produrre una singolarità, ovvero un punto in cui il vettore è nullo.

Un teorema di punto fisso è un teorema che garantisce che una data funzione  abbia un punto fisso, ovvero un  tale che .

Interpretando  come funzione che sposta i punti, un punto fisso è un punto che non si muove.

I teoremi di punto fisso sono utili in molte aree della matematica,

ad esempio

in analisi possono essere utili per dimostrare l’esistenza di una soluzione di una particolare equazione differenziale.

Il teorema del punto fisso di Brouwer 

asserisce che se  è una palla chiusa di dimensione arbitraria  e  è continua, allora un punto fisso esiste sempre.

Il teorema è intrinsecamente topologico e resta quindi valido per ogni spazio  omeomorfo a una palla chiusa, quale un quadrato, un poliedro convesso, ecc.

Il teorema può essere dimostrato con l’omologia.

Due teoremi correlati sono il teorema di Borsuk-Ulam e il teorema del panino al prosciutto.

Sugli assiomi di separazione

Gli assiomi di separazione T0, T1, T2, … sono degli assiomi aggiuntivi che garantiscono una maggiore “regolarità” allo spazio topologico in esame.

Ciascun assioma è un raffinamento del precedente.

Ci sono in topologia vari teoremi molto generali, che hanno però bisogno che alcuni di questi assiomi siano soddisfatti.

Lemma di Urysohn

Se lo spazio topologico  in esame è T4, gli insiemi chiusi possono essere “separati” tramite una funzione continua a valori in un intervallo reale.

Cioè,

per ogni coppia di chiusi  disgiunti esiste una funzione continua

che valga 1 su  e 0 su .

Il lemma di Urysohn

è considerato spesso il primo risultato non banale in topologia.

Può essere usato

(se sono validi anche gli assiomi di numerabilità) per dare a  una struttura di spazio metrico.

Teorema di estensione di Tietze

Se lo spazio topologico  è T4, ogni funzione continua a valori reali definita su un sottoinsieme chiuso può essere estesa ad una funzione continua su .

Questo teorema è conseguenza del lemma di Urysohn.

°°°°°

Sugli spazi metrici

Teorema delle categorie di Baire

Uno spazio metrico completo è sempre uno spazio di Baire.

Questo risultato implica in particolare che  non può essere unione numerabile di chiusi con parte interna vuota (ma  sì).

Settori

Topologia generale

La topologia generale è il settore di base.

Si occupa degli spazi topologici e delle loro proprietà generali ed è il più vicino alla teoria degli insiemi.

Si interessa quindi in particolare delle nozioni di:

intorno,

parte interna,

chiusura,

compattezza,

connessione,

successioni,

reti,

spazi metrici,

funzioni continue,

assiomi di separazione

assiomi di numerabilità.

°°°°°

Topologia algebrica

La topologia algebrica applica gli strumenti dell’algebra alla topologia.

La nozione fondamentale è quella di invariante topologico,

un oggetto algebrico che caratterizza alcune proprietà dello spazio topologico in esame.

Fra gli invarianti più usati ci sono il gruppo fondamentale

(e i più generali gruppi di omotopia) e l’omologia.

La topologia algebrica studia più in generale

la nozione di omotopia e vari concetti correlati quali il grado topologico.

°°°°°

Topologia differenziale

La topologia differenziale si occupa essenzialmente di varietà differenziabili e applica gli strumenti del calcolo infinitesimale al loro studio.

Con questi strumenti si definiscono e studiano:

campi vettoriali,

spazio tangente,

fibrati vettoriali,

forme differenziali

i più generali tensori.

°°°°°

Topologia in dimensione bassa

La topologia in dimensione bassa è un settore più recente, esploso alla fine degli anni settanta.

Gli oggetti studiati sono le varietà di dimensione bassa, ovvero 1,2,3,4.

Una branca importante è

la teoria dei nodi.

°°°°°

 

 

 

 

 

Segue …

Nome(obbligatorio)

E-mail(obbligatorio)

Sito web

Messaggio

Invia

Δ

 

Elementi di geometria analitica

Diagramma di Eulero di alcuni insiemi numerici notevoli

°°°°°

“La matematica non conosce razze o confini geografici; per la matematica, il mondo culturale è una singola nazione.”

DAVID HILBERT

°°°°°

Elementi di geometria analitica

La geometria (dal greco antico ” γεωμετρία” , composto dal prefisso geo che rimanda alla parola γή = “terra” e μετρία , metria = “misura”, quindi letteralmente come misurazione della terra ) è quella parte della scienza matematica che si occupa delle forme nel piano e nello spazio e delle loro mutue relazioni.

Cenni storici

La nascita della Geometria risale all’epoca degli antichi egizi .

Erodoto racconta che a causa dei fenomeni di erosione e di deposito dovuti alle piene del Nilo , all’interno delle proprietà terriere egiziane variavano ogni anno e dovevano quindi essere ricalcolate a fini fiscali.

Nacque così il bisogno di inventare tecniche di misura della terra ( geometria nel significato originario del termine).

Lo sviluppo della Geometria pratica è molto antico, per le numerose applicazioni che consente e per le quali è stata sviluppata, e in epoche remote fu a volte riservata a una categoria di sapienti con attribuzioni sacerdotali. Presso l ‘ Antica Grecia , soprattutto per via dell’influenza del filosofo ateniese Platone e, ancor prima di lui, di Anassimandro di Mileto ^{[ senza fonte ]} , si diffuse massicciamente l’ uso della riga e del compasso (sebbene pare che questi strumenti fossero già stati inventati altrove) e, soprattutto, nacque l’idea nuova di usare tecniche dimostrative. La geometria greca servì da base per lo sviluppo dellageografia , dell ‘ astronomia , dell’ ottica , della meccanica e di altre scienze, nonché di varie tecniche, come quelle per la navigazione .

Nella civiltà greca , oltre alla geometria euclidea che si studia ancora a scuola, e alla teoria delle coniche, nacquero anche la geometria sferica e la trigonometria (piana e sferica ).

°°°°°

Geometria euclidea

La geometria coincide fino all’inizio del XIX secolo con la geometria euclidea. Questa definisce come i primitivi il punto , la retta e il piano , e assume la veridicità di alcuni assiomi , gli assiomi di Euclide . Da questi assiomi vengono quindi dedotti dei teoremi anche complessi, come il teorema di Pitagora ed i teoremi della geometria proiettiva .

La scelta dei settori primitivi e degli assiomi è motivata dal desiderio di rappresentare la realtà, e in particolare gli oggetti nello spazio tridimensionale in cui viviamo. Concetti primitivi come la retta ed il piano vengono informalmente come “fili e fogli di carta senza spessore”, e l’altro canto molti oggetti della vita reale vengono idealizzati tramite enti geometrici come il triangolo o la piramide . In questo modo, i teoremi fin dall’antichità degli strumenti utili per le discipline che riguardano lo spazio in cui viviamo: meccanica , architettura , geografia , navigazione , astronomia .

Geometria piana

La geometria piana si occupa delle figure geometriche nel piano. A partire dal concetto primitivo di retta, vengono costruiti i segmenti , e quindi i poligoni come il triangolo , il quadrato , il pentagono , l’ esagono , ecc.

Le quantità numeriche importanti nella geometria piana sono la lunghezza , l’ angolo e l’ area . Ogni segmento ha una lunghezza, e due segmenti che si incontrano in un estremo integrati un angolo. Ogni poligono ha un’area. Molti teoremi della geometria piana mettono in relazione le lunghezze, angoli e aree presenti in alcune figure geometriche. Ad esempio, la somma degli angoli interni di un triangolo risulta essere un angolo piatto , e l’area di un rettangolo si esprime come prodotto delle lunghezze dei segmenti di base e altezza . La trigonometria studia le relazioni fra gli angoli e le lunghezze.

Geometria solida

La geometria solida (o stereometria) studia le costruzioni geometriche nello spazio. Con segmenti e poligoni si costruiscono i poliedri , come il tetraedro , il cubo e la piramide .

I poliedri hanno vertici, spigoli e facce. Ogni spigolo ha una lunghezza, ed ogni faccia ha un’area. In più, il poliedro ha un volume . Si parla inoltre di angoli diedrali per esprimere l’angolo formato da due facce adiacenti in uno spigolo. Molti teoremi mettono in relazione queste quantità: ad esempio il volume della piramide può essere espresso nell’area della figura di base e la lunghezza dell’altezza.

Figura curva

La geometria euclidea considera anche alcune figure curve. Le figure “base” sono la circonferenza nel piano e la sfera nello spazio, definito come luogo dei punti equidistanti da un punto fissato. Partendo da queste figure, ne vengono definite altre come il cono . A queste figure vengono associate grandezze analoghe ai poliedri: si parla quindi di length della circonferenza, di area del cerchio e di volume della sfera.L’intersezione nello spazio di un cono con un piano forma una nuova figura curvilinea: a seconda dell’inclinazione del piano, questa è una ellisse , una parabola , un ‘ iperbole o una circonferenza . Queste sezioni coniche sono le curve più semplici realizzabili nel piano. Ruotando una figura intorno ad una retta, si ottengono altre figure curve. Ad esempio, ruotando un’ellisse o una parabola si ottengono l’ ellissoide ed il paraboloide. Anche in questo caso, il volume dell’oggetto può essere messo in relazione con altre quantità. La geometria euclidea non fornisce però sufficienti strumenti per dare una corretta definizione di lunghezza e area per molte figure curve.

°°°°°

Geometria cartesiana

La geometria cartesiana (o analitica) ingloba le figure ed i teoremi della geometria euclidea, introducendone di nuovi grazie a due importanti discipline della matematica: l ‘ algebra e l’ analisi . Lo spazio (ed il piano) sono rappresentati con delle coordinate cartesiane . In questo modo ogni figura geometrica è descrivibile tramite una o più equazioni (o disequazioni ).

Rette e piani sono oggetti risultanti da equazioni di primo grado , mentre le coniche sono definite tramite equazioni di secondo grado . Equazioni polinomiali di grado superiore definiscono nuovi oggetti curvi. Il calcolo infinitesimale permette di estendere con precisione i progetti di lunghezza e area a queste nuove figure. L ‘ integrale è un utile strumento analitico per determinare queste quantità. Si parla in generale quindi di curve e superfici nel piano e nello spazio.

Spazi vettoriali

Retta (passante per l’origine), piano (contenente l’origine) e spazio sono esempi di spazi vettoriali di dimensione rispettivamente 1, 2 e 3: infatti ogni punto è esprimile rispettivamente con 1, 2 o 3 coordinate. La geometria cartesiana è facilmente estendibile alle dimensioni superiori: in questo modo si definiscono spazi di dimensione 4 e oltre, come insiemi di punti aventi 4 o più coordinate.

Grazie all ‘ algebra lineare , lo studio delle rette e dei piani nello spazio può essere esteso allo studio dei sottospazi di uno spazio vettoriale, di dimensione arbitraria. Lo studio di questi oggetti è collegato a quello dei sistemi lineari e delle loro soluzioni. In dimensione più alta, alcuni risultati possono contrastare con l’intuizione geometrica tridimensionale a cui siamo abituati. Ad esempio, in uno spazio di dimensione 4, due piani possono intersecarsi in un punto solo.

°°°°°

Geometria affine

In uno spazio vettoriale l’origine (cioè il punto da cui provengono gli assi, di coordinate tutte nulle) gioca un ruolo fondamentale: per poter usare in modo efficace l’ algebra lineare , si considera infatti solo sottospazi passanti per l’origine. In questo modo si ottengono delle relazioni eleganti fra i sottospazi, come la formula di Grassmann .

Nella geometria affine il ruolo predominante dell’origine è abbandonato. I sottospazi non sono vincolati, e possono quindi essere paralleli: questa crea una quantità considerevole di casistiche in più. In particolare, la formula di Grassmann non è più valida. Lo spazio affine è considerato (fino alla scoperta della relatività ristretta ) come lo strumento migliore per creare modelli dell’universo, con 3 dimensioni spaziali ed eventualmente 1 dimensione temporale, senza “origini” o punti privilegiati.

°°°°°

Geometria algebrica

Dal XIX secolo in poi l’algebra diventa uno strumento preponderante per lo studio della geometria. Nel tentativo di “abbellire” il quadro, e di ricondurre molte proprietà e teoremi ad un numero sempre minore di proprietà fondamentali, la geometria analitica viene progressivamente inglobata in un concetto più ampio di geometria: si aggiungono i “punti all’infinito” così la geometria proiettiva ), e si fanno variare le coordinate di un punto non solo nei numeri reali , ma anche in quelli complessi .

Geometria proiettiva

La geometria proiettiva nasce come strumento legato al disegno in prospettiva , e viene formalizzata nel XIX secolo come un arricchimento della geometria cartesiana. La geometria proiettiva include i “punti all’infinito” ed elimina quindi alcune casistiche considerate fastidiose, come la presenza di rette parallele.

In questa geometria molte situazioni si semplificano: due piani distinti si intersecano sempre in una retta, e oggetti differenti della geometria analitica (come le coniche ellisse, parabola e iperbole) risultano essere equivalenti in questo nuovo contesto. La geometria proiettiva è anche un esempio di compattificazione : similmente a quanto accade con la proiezione stereografica , aggiungendo i punti all’infinito lo spazio diventa compatto , cioè “limitato”, “finito”.

Varietà algebriche

La geometria algebrica verte essenzialmente sullo studio dei polinomi e delle loro radici : gli oggetti che tratta, chiamate varietà algebriche , sono gli insiemi dello spazio proiettivo , affine o euclideo definiti come luoghi di zeri di polinomi.Nel XX secolo il concetto di varietà algebrica assume un’importanza sempre maggiore. Rette, piani, coniche, ellissoidi, sono tutti esempi di varietà algebriche. Lo studio di questi oggetti raggiunge risultati impressionanti quando le coordinate dello spazio vengono fatte variare nel campo dei complessi complessi : in questo caso, grazie al teorema fondamentale dell’algebra , un polinomio ha semper delle radici.This Fatto algebrico di grande Importanza (esprimibile Dicendo Che i numeri Codice Complessi Formano un campo algebricamente chiuso ) ha venuto conseguenza la Validità di ALCUNI Teoremi potenti di Carattere molto generale. Ad esempio, il teorema di Bézout asserisce che due curve di grado e nel piano che non hanno componenti in comune si intersecano sempre in punti, contanti con un’opportuna molteplicità. Questo risultato necessita che il “piano” sia proiettivo e complesso. In particolare, è certamente falso nell’ambito classico della geometria analitica: due circonferenze non devono intersecarsi necessariamente in 4 punti, possono anche essere disgiunte. Lo studio della geometria nello spazio proiettivo complesso aiuta anche a capire la geometria analitica classica. Le curve nel piano cartesiano reale possono ad esempio essere viste come “sezioni” di oggetti più grandi, contenuti nel piano proiettivo complesso, ed i teoremi generali validi in questo “mondo più vasto e perfetto” si riflettono nel piano cartesiano, pur in modo meno elegante. Come lo studio della geometria affine fa largo uso dell’algebra lineare , quello delle varietà algebriche attinge a piene mani dall’algebra commutativa .

°°°°°

Geometria differenziale

La geometria differenziale è lo studio di oggetti geometrici tramite l ‘ analisi . Gli oggetti geometrici non sono definiti da polinomi (come nella geometria algebrica), ma sono ad esempio curva e superfici , cioè oggetti che, visti localmente con una lente di ingrandimento, sembrano quasi rettilinei o piatti. Oggetti cioè “senza spessore”, e magari un po ‘curvi. Come la superficie terrestre, che all’uomo sembra piatta, benché non lo sia.

Questo concetto di “spazio curvo” è espresso tramite la nozione di varietà differenziabile . La sua definizione non necessita neppure di “vivere” in uno spazio ambiente, ed è quindi usata ad esempio nella relatività generale per descrivere intrinsecamente la forma dell’universo. Una varietà può essere dotata di una proprietà fondamentale, la curvatura , che viene misurata tramite oggetti matematici molto complessi, come il tensore di Riemann . Nel caso in cui lo spazio sia una curva o una superficie, questi oggetti matematici risultano più semplici: si parla ad esempio di curvatura gaussiana per le superfici.

Su una varietà dotata di curvatura, detta varietà riemanniana , sono definite una distanza fra punti, e le geodetiche : queste sono curve che modellizzano i percorsi localmente più brevi, come le rette nel piano, oi meridiani sulla superficie terrestre.

°°°°°

Geometrie non euclidee

Con la geometria differenziale è possibile costruire un “piano” in cui valgono tutti i postulati di Euclide , tranne il quinto , quello delle parallele . Questo postulato ha avuto un’importanza storica fondamentale, perché ci sono voluti 2000 anni per dimostrare la sua effettiva indipendenza dai precedenti. Asserisce che, fissati una retta ed un punto non contenuto in , esiste un’unica retta parallela a e passante per . 

Una geometria non euclidea è una geometria in cui valgono tutti gli assiomi di Euclide, tranne quello delle parallele. La sfera , con le geodetiche che svolgono il ruolo delle rette, fornisce un esempio semplice di geometria non euclidea: due geodetiche si intersecano semper in due points antipodali , e quindi non ci sono rette parallele. Un tale esempio di geometria è detta ellittica . Esistono anche esempi opposti, in cui ci sono “così tante” rette parallele, che le rette parallele a e passanti per sono infinite (e non una). Questo tipo di geometria è detta iperbolica , ed è più difficile da descrivere concretamente. 

°°°°°

Topologia

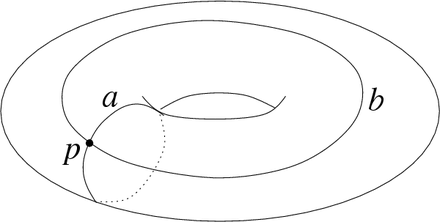
La topologia è infine lo studio delle forme, e di tutte quelle proprietà degli enti geometrici che non cambiano quando questi vengono deformati in modo continuo, senza strappi. La topologia studia tutti gli oggetti geometrici (definiti in modo algebrico, differenziale, o quant’altro) guardando solo la loro forma. Distingue ad esempio la sfera dal toro , perché quest’ultimo ha “un buco in mezzo”. Studia le proprietà di connessione (spazi “fatti di un pezzo solo”) e di compattezza (spazi “limitati”), e le funzioni continue fra questi.

Le forme degli oggetti vengono codificate tramite oggetti algebrici, come il gruppo fondamentale : un gruppo che codifica in modo raffinato la presenza di “buchi” in uno spazio topologico .

°°°°°

Geometria e geometrie

Nel 1872 Felix Klein elaborò un programma di ricerca, l’ Erlanger Programm , in grado di produrre una grande sintesi delle conoscenze geometriche e integrarle con altri settori della matematica, quali la teoria dei gruppi .

Nella prospettiva di Klein una geometria consiste nello studio di proprietà di uno spazio che sono invarianti rispetto ad un gruppo di trasformazioni ( geometria delle trasformazioni ):

• La geometria euclidea si occupa di proprietà che sono invarianti rispetto a isometrie , cioè trasformazioni che preservano lunghezze e angoli.

• La geometria affine si occupa di proprietà che sono invarianti per trasformazioni affini . In ambito di geometria affine non ha più senso il concetto di “angolo” o di “length” e tutti i triangoli sono “equivalenti”.

• La geometria proiettiva studia le proprietà che sono invarianti per trasformazioni proiettive , cioè trasformazioni che possono essere ottenute mediante proiezioni. In ambito proiettivo tutte le coniche sono equivalenti potendo essere trasformata l’una nell’altra da una proiezione.

• La topologia studia proprietà che sono invarianti per deformazioni continue . Dal punto di vista topologico una tazza ed una ciambella diventano equivalenti potendo essere deformate l’una nell’altra ma si distinte da una sfera che non può essere “bucata” senza una trasformazione discontinua.

Applicazioni

La geometria analitica e l’ algebra lineare importano collegamenti tra l’intuizione geometrica e il calcolo algebrico che sono diventati ormai una parte costitutiva di tutta la matematica moderna e delle sue applicazioni in tutte le scienze. La geometria differenziale ha trovato importanti applicazioni nella costruzione di modelli per la fisica e per la cosmologia . La geometria piana e dello spazio fornisce inoltre degli strumenti per modellizzare, progettare e costruire oggetti reali nello spazio tridimensionale: è quindi di fondamentale importanza in architettura e in ingegneria come anche nel disegnoe nella computer grafica .

°°°°°

Geometria descrittiva

La geometria descrittiva è una disciplina che permette, attraverso determinate costruzioni grafiche, di rappresentare oggetti tridimensionali già esistenti ( rilievo ) e / o da costruire ( progettazione ). L’applicazione informatizzata della geometria descrittiva permette oggi la creazione di superfici e solidi, anche ad alta complessità tridimensionale . Inoltre, e soprattutto, ne permette il controllo in modo inequivocabile di ogni loro forma e dimensione . I maggiori campi d’Impiego della geometria descrittiva Sono Quelli dell ‘ architettura , dell’ ingegneria e Quelli deldesign industriale.

°°°°°

 

 

 

 

 

Segue …

Nome(obbligatorio)

E-mail(obbligatorio)

Sito web

Messaggio

Invia

Δ

 

iMathematica

INTRODUZIONE ALLA MATEMATICA SUPERIORE

“La differenza tra il poeta e il matematico è che il poeta cerca di infilare la testa nel cielo, mentre il matematico cerca di infilare il cielo nella sua testa.”

(GK Chesterton)

°°°°°

Se ascolto qualcosa, la dimentico. Se la vedo, la ricordo. Se la faccio, la imparo.

°°°°°

Premessa:

Insieme Aperto in R

Insieme Chiuso in R

X : Intorno di un punto x_o di R^k

x_o :  punto interno a X

x_o :  punto esterno a X

x_o :  punto aderente a X

x_o :  punto di accumulazione per X

x_o :  punto isolato per X

x_o :  punto di Frontiera per X

°°°°°

°°°°°

°°°°°

“La conoscenza matematica aggiunge vigore alla mente, e la libera da pregiudizi, credulità e superstizione.”

(John Arbuthnot)