
Capitolo V.
” Il mio scopo principale é stato di conciliare il rigore, al quale mi ero attenuto nel mio Corso di Analisi, con la semplicità che deriva immediatamente dalla considerazione delle quantità infinitesime.”

§ V.1.- Funzioni continue in uno spazio metrico .-
V.11.-
Sia  uno spazio metrico
uno spazio metrico
Sia  uno spazio metrico
uno spazio metrico
Consideriamo
la direzione x→a formate dalle sfere  escluso il punto a .-
escluso il punto a .-
°°°°°
V.11.a.- Definizione di funzione continua per x=a.- Il punto x=a si chiama punto di continuità della funzione
Il punto x=a si chiama punto di continuità della funzione
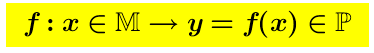 °°°°°
°°°°°
Se 
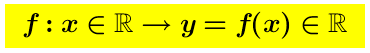
quindi f(x) é una funzione numerica, allora:

°°°°°
V.11.b.- Dal punto IV.66 segue la seconda definizione di continuità

°°°°°
V.11.c.- Ogni punto isolato a∈M é, per definizione, punto di continuità della funzione f(x).
°°°°°
V.11.d.- Definizione.-
°°°°°
V.11.e.-Definizione.-
°°°°°
V.11.f.- La definizione di continuità della funzione f(x) nel punto a∈M dipende, ovviamente, dalla metrica data sugli spazi metrici
 e
e
 Ma poiché questa definizione può essere formulata nei termini di successioni convergenti (V.11.b), la proprietà di una funzione di essere continua in un punto x=a, così come su tutto l’insieme M non é violata sostituendo le metriche degli spazi metrici
Ma poiché questa definizione può essere formulata nei termini di successioni convergenti (V.11.b), la proprietà di una funzione di essere continua in un punto x=a, così come su tutto l’insieme M non é violata sostituendo le metriche degli spazi metrici
 e
e
 con quelle omomorfe (III.34).
con quelle omomorfe (III.34).
°°°°°
V.12.a.- Un esempio evidente di una funzione continua avente
 come dominio di definizione e
come dominio di definizione e
 come dominio di valori é fornito da una funzione costante
come dominio di valori é fornito da una funzione costante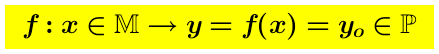 dove
dove  é un punto fisso dello spazio
é un punto fisso dello spazio

°°°°°
V.12.b.- Come secondo esempio, consideriamo la distanza ρ(x, a) da un punto fisso a.
Questa é una funzione numerica nello spazio metrico M.
°°°°°
figura 1
°°°°°
Alcune nozioni fondamentali …
In matematica, una palla (o bolla, o intorno circolare) è un sinonimo di sfera, che gli viene preferito nel caso di spazi non tridimensionali e per gli spazi metrici in generale.
Spazi metrici
La palla (aperta) di raggio r > 0 centrata nel punto p di M è definita come
-

dove d è la distanza o metrica.
Se il simbolo di minore (<) è sostituito dal simbolo di minore o uguale (≤), la definizione precedente diventa quella di una
palla chiusa di raggio r > 0 centrata nel punto p di M è definita come:
-
 .
.
Occorre comunque prestare attenzione al fatto che la chiusura di una palla aperta  in generale non coincide con la palla chiusa
in generale non coincide con la palla chiusa  ma è inclusa strettamente.
ma è inclusa strettamente.
D’altronde, un elemento x di  appartiene alla sua chiusura se e solo se esiste una successione di elementi di
appartiene alla sua chiusura se e solo se esiste una successione di elementi di  di cui x è il limite.
di cui x è il limite.
Può essere che  ma non esistere una successione suddetta.
ma non esistere una successione suddetta.
Nota in particolare che una palla (aperta o chiusa) include sempre p stesso, poiché r > 0.
Una palla unitaria (aperta o chiusa) è una palla di raggio 1.
Nello spazio euclideo n-dimensionale con l’ordinaria metrica euclidea, se lo spazio è la retta, la palla è un intervallo, e se lo spazio è il piano, la palla è il disco interno a un cerchio. Gli oggetti a quattro dimensioni e superiori sono chiamati iperpalla e ipersfera. Vedi quest’ultima per “volume” e “area”.
Con altre metriche la forma di una palla può essere differente, ad esempio:
-
in 2 dimensioni:
-
con la norma 1 (cioè nella geometria Manhattan) una palla è un quadrato con le diagonali parallele agli assi coordinati
-
con la distanza di Chebyshev una palla è un quadrato con i lati paralleli agli assi coordinati
-
in 3 dimensioni:
-
con la norma 1 una palla è un ottaedro regolare con le diagonali interne parallele agli assi coordinati
-
con la distanza di Chebyshev una palla è un cubo con gli spigoli paralleli agli assi coordinati
Nota che in molti casi le palle ruotate non sono palle.
°°°°°
Definizioni Punto interno
Se S è un sottoinsieme di uno spazio euclideo, allora x è un punto interno di S se esiste una palla aperta centrata in x e contenuta in S.
Questa definizione si generalizza a ogni sottoinsieme S di uno spazio metrico X. Espressa per intero, se X è uno spazio metrico con metrica d, allora
x è un punto interno di S se esiste r > 0 tale che y sia in S ogni volta che la distanza è d(x, y) < r.
Questa definizione si generalizza a uno spazio topologico sostituendo la “palla aperta” con “intorno“. Sia S un sottoinsieme di uno spazio topologico X. Allora
x è un punto interno di S se esiste un intorno di x contenuto in S.
Nota che questa definizione non dipende dal fatto che gli intorni siano aperti oppure no.
°°°°°
Definizione Punto aderente
Un punto  è aderente ad
è aderente ad  se comunque si prenda un intorno dell’elemento
se comunque si prenda un intorno dell’elemento  , l’intersezione dell’intorno con l’insieme
, l’intersezione dell’intorno con l’insieme  è sempre non vuota.
è sempre non vuota.
Spazi topologici
Un punto  appartenente ad uno spazio topologico
appartenente ad uno spazio topologico  è detto punto di aderenza (o punto di chiusura) per un sottoinsieme
è detto punto di aderenza (o punto di chiusura) per un sottoinsieme  di
di  se ogni aperto contenente
se ogni aperto contenente  interseca
interseca  . In simboli:
. In simboli:
-

Spazi metrici
In uno spazio metrico, se si considera la topologia naturalmente indotta dalla metrica, la definizione è equivalente alla richiesta seguente.
-
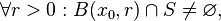
dove con  si indica la palla di raggio
si indica la palla di raggio  e centro
e centro  .
.
Non ne consegue (come nel caso dei punti di accumulazione) che in ogni palla vi siano infiniti punti di 
°°°°°
Definizione di Frontiera (topologia)
la frontiera o contorno di un sottoinsieme S di uno spazio topologico X è la chiusura dell’insieme meno il suo interno.
Un elemento della frontiera di S è chiamato punto di frontiera di S.
Le notazioni usate per indicare la frontiera di un insieme S includono bd(S), fr(S), e  .
.
Esistono altri due modi equivalenti per definire la frontiera di S e i punti di frontiera di S.
Si definisce frontiera di S l’intersezione fra la chiusura di S e la chiusura del suo complementare.
Si definisce frontiera di S l’insieme dei punti p in X tali che ogni intorno di p contiene almeno un punto di S e almeno un punto non appartenente a S
°°°°°
Definizione di Punto di Accumulazione
Dato l’insieme 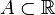 e
e  (non interessa che
(non interessa che  appartenga ad
appartenga ad  o meno), si dice che
o meno), si dice che  è punto di accumulazione per l’insieme
è punto di accumulazione per l’insieme  se in ogni intorno
se in ogni intorno  di
di  esiste almeno un elemento
esiste almeno un elemento  diverso da
diverso da  ed appartenente ad
ed appartenente ad  .
.
In formule:

Intuitivamente questo significa che se facciamo uno zoom su  continuiamo a vedere punti di
continuiamo a vedere punti di  (diversi da
(diversi da  ) a qualsiasi livello di ingrandimento.
) a qualsiasi livello di ingrandimento.
Generalizzazioni
La nozione di punto di accumulazione è generalizzata agli spazi metrici e topologici; in entrambi i casi un punto  è di accumulazione per un insieme
è di accumulazione per un insieme  se l’insieme
se l’insieme  contiene punti “arbitrariamente vicini” ad
contiene punti “arbitrariamente vicini” ad  . La nozione di “arbitrariamente vicino” è formalizzata in modo appropriato, a seconda che lo spazio sia munito di una metrica o soltanto di una topologia.
. La nozione di “arbitrariamente vicino” è formalizzata in modo appropriato, a seconda che lo spazio sia munito di una metrica o soltanto di una topologia.
Spazi topologici
In topologia un punto  appartenente ad uno spazio topologico
appartenente ad uno spazio topologico  è un punto di accumulazione per un sottoinsieme
è un punto di accumulazione per un sottoinsieme  di
di  se qualsiasi aperto
se qualsiasi aperto  contenente
contenente  interseca
interseca  in almeno un punto diverso da
in almeno un punto diverso da  . In simboli:
. In simboli:
-
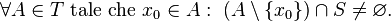
Spazi metrici
In uno spazio metrico, se si considera la topologia naturale indotta dalla metrica, la definizione introdotta precedentemente è equivalente alla seguente:
-

dove  è la palla di raggio
è la palla di raggio  e centro
e centro  . In altre parole, ogni palla centrata in
. In altre parole, ogni palla centrata in  interseca
interseca  in qualche punto diverso da
in qualche punto diverso da  .
.
Nel caso di spazi metrici, se  è punto di accumulazione per
è punto di accumulazione per  , allora è possibile trovare punti di
, allora è possibile trovare punti di  , distinti da
, distinti da  a distanza arbitrariamente piccola da
a distanza arbitrariamente piccola da  . Dunque in ogni intorno di
. Dunque in ogni intorno di  cadono infiniti punti di
cadono infiniti punti di  .
.
Nozioni correlate
L’insieme dei punti di accumulazione di  è detto insieme derivato di
è detto insieme derivato di  e si indica di solito con
e si indica di solito con  .
.
°°°°°
Definizione di Punto isolato
Un punto  appartenente ad un sottoinsieme
appartenente ad un sottoinsieme  in uno spazio topologico è un punto isolato di
in uno spazio topologico è un punto isolato di  se esiste un intorno di
se esiste un intorno di  non contenente altri punti di
non contenente altri punti di  .
.
Spazio metrico o euclideo
è un punto isolato di  se esiste una palla aperta centrata in
se esiste una palla aperta centrata in  che non contiene nessun elemento di
che non contiene nessun elemento di  diverso da
diverso da  .
.
Definizioni equivalenti
In modo equivalente, un punto  di
di  non è un punto isolato se e solo se
non è un punto isolato se e solo se  è un punto di accumulazione per
è un punto di accumulazione per  .
.
Insieme discreto
Un insieme  costituito esclusivamente di punti isolati è detto insieme discreto.
costituito esclusivamente di punti isolati è detto insieme discreto.
Ogni insieme finito in uno spazio metrico è discreto.
Il viceversa è vero
se lo spazio metrico è compatto e  è chiuso:
è chiuso:
in uno spazio compatto, ogni sottoinsieme chiuso discreto è finito.
Un sottoinsieme discreto in uno spazio non compatto può non essere finito, ma generalmente è numerabile: questo accade ad esempio nello spazio euclideo.
D’altra parte,
non è vero che ogni sottoinsieme numerabile dello spazio euclideo è discreto: ad esempio l’insieme  dei numeri razionali è numerabile ma non discreto.
dei numeri razionali è numerabile ma non discreto.
Insieme perfetto
Un insieme chiuso senza punti isolati, costituito da soli punti di accumulazione, è detto insieme perfetto.
Esempi
Ogni elemento di 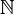 è isolato in
è isolato in 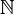 infatti: Sia
infatti: Sia  e sia
e sia  un intorno di
un intorno di 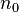 e di raggio
e di raggio  .
.
Allora dalla definizione abbiamo che  è un punto isolato in
è un punto isolato in 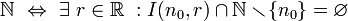 .
.
Poiché per  risulta che
risulta che  , deduciamo che
, deduciamo che 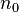 è isolato.
è isolato.
Gli spazi topologici dei seguenti esempi sono da considerare sottospazi della retta reale.
°°°°°

…Segue…
“……..”
Tag: Capitolo V, Funzioni continue in uno Spazio Metrico, palla (aperta) di raggio r > 0 centrata nel punto p di M, palla chiusa di raggio r > 0 centrata nel punto p di M, Punto aderente, punto di accumulazione, punto di continuità della funzione, punto di frontiera, Punto interno, punto isolato

V. Funzioni continue
” Il mio scopo principale é stato di conciliare il rigore, al quale mi ero attenuto nel mio Corso di Analisi, con la semplicità che deriva immediatamente dalla considerazione delle quantità infinitesime.”
9.19. – Funzioni continue in uno Spazio Metrico.-
Sia M uno spazio metrico
Sia P uno spazio metrico
Sia data una funzione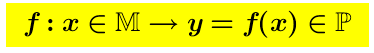 Sia a∈M un punto fisso non isolato.
Sia a∈M un punto fisso non isolato.
Consideriamo la direzione x→a formate dalle sfere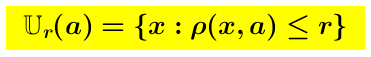 escluso il punto a .
escluso il punto a .
9.19.1. – Definizione.- Osservazione 1
Osservazione 1
Se 
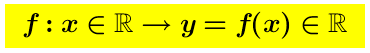
 Osservazione 2
Osservazione 2
segue la seconda definizione di continuità
9.19.2. – Definizione.-
Osservazione 3
Ogni punto isolato a∈M é, per definizione, punto di continuità della funzione f(x).
9.19.3. – Definizione.-
9.19.4. – Definizione.- Osservazione 4
Osservazione 4
La definizione di continuità della funzione f(x) nel punto a∈M dipende, ovviamente, dalla metrica data sugli spazi metrici M e P.
Ma poichè questa definizione può essere formulata nei termini di successioni convergenti, la proprietà di una funzione di essere continua in un punto a, così come su tutto l’insieme M non é violata sostituendo le metriche dgli spazi metrici M e P con quelle omomorfe.
9.19.5a. – Un esempio evidente di una funzione continua avente M come dominio di definizione e P come dominio di valori é fornito da una funzione costante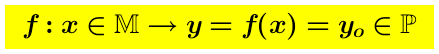 dove
dove  é un punto fisso dello spazio P.
é un punto fisso dello spazio P.
9.19.5b. – Come secondo esempio, consideriamo la distanza ρ(x,a) da un punto fisso a. Questa é una funzione numerica nello spazio metrico M. La sua continuità in ogni punto 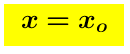 dello spazio M deriva dalla relazione
dello spazio M deriva dalla relazione
°°°
9.19.6. –
Le proposizioni seguenti relative al caso di funzioni numeriche permettono di costruire larghe classi di funzioni continue.
a.-
Se  Se
Se anche
anche b.-
b.-
Se  Se
Se anche
anche c.-
c.-
Se  Se
Se Se
Se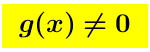 anche
anche d.-
d.-
La funzione numerica y=x , definita sulla retta numerica R, é evidentemente continua su R. Dalle proposizioni a.-, b.-, c.- segue che:
Ogni polinomio 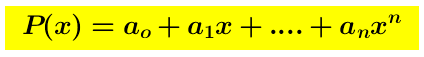 é continuo dappertutto su R.
é continuo dappertutto su R.
Ogni funzione razionale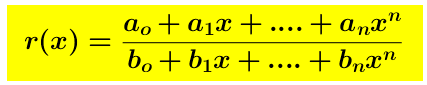 é continua dappertutto su R, tranne nei punti in cui il suo denominatore si annulla.
é continua dappertutto su R, tranne nei punti in cui il suo denominatore si annulla.
e.-
La funzione numerica 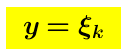 (la k-esima coordinata del vettore
(la k-esima coordinata del vettore  ) é, evidentemente, continua nello spazio a n dimensioni
) é, evidentemente, continua nello spazio a n dimensioni 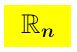 Dalle proposizioni a.-, b.-, c.- segue che:
Dalle proposizioni a.-, b.-, c.- segue che:
Ogni polinomio nelle coordinate del vettore  é continuo dappertutto in
é continuo dappertutto in
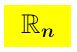 Dalle proposizioni a.-, b.-, c.- segue che:
Dalle proposizioni a.-, b.-, c.- segue che:
Ogni funzione razionale delle coordinte del vettore é continua dappertutto in
é continua dappertutto in
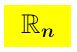 tranne nei punti in cui il suo denominatore si annulla.
tranne nei punti in cui il suo denominatore si annulla.
9.19.7. –
Sia data una funzione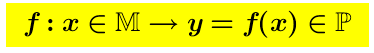 continua su M.
continua su M.
Sia 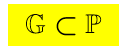 un insieme e
un insieme e
Sia .
.
1a.-
1b.-
1c.- Conseguenza.
Se 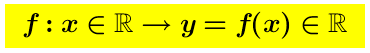 é continua,
é continua,  sono insiemi aperti.
sono insiemi aperti.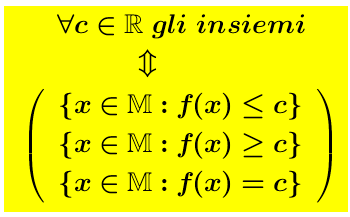 sono insiemi chiusi.
sono insiemi chiusi.
1d.-
Se sono funzioni continue, per quali che siano
sono funzioni continue, per quali che siano e
e l’insieme
l’insieme é aperto.
é aperto.
l’insieme é chiuso.
é chiuso.
1e.-
In virtù della proposizione 1d.-, numerose figure dell geometria elementare descritte dai sistemi di disuguaglianze:
 sono, rispettivamente, aperte o chiuse. Così, in uno spazio a n dimensioni, un insieme della forma
sono, rispettivamente, aperte o chiuse. Così, in uno spazio a n dimensioni, un insieme della forma é aperto e si chiama rettangolo aperto.
é aperto e si chiama rettangolo aperto.
Un insieme della forma é chiuso e si chiama rettangolo chiuso.
é chiuso e si chiama rettangolo chiuso.
Osservazione 5
In uno spazio a n=2 dimensioni
Un poligono a m lati descritto da m disuguaglianze della forma: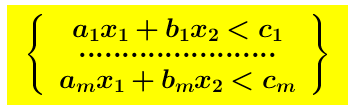 é un insieme aperto, ossi un poligono a m lati aperto.
é un insieme aperto, ossi un poligono a m lati aperto.
Un poligono a m lati descritto da m disuguaglianze della forma: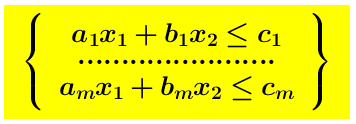 é un insieme chiuso, ossi un poligono a m lati chiuso.
é un insieme chiuso, ossi un poligono a m lati chiuso.
Osservazione 6
In uno spazio a n dimensioni,
sono definiti i poliedri aperti e poliedri chiusi da disuguaglianze che legano le funzioni lineari di coordinate.
Osservazione 7
Fra le figure menzionate, quelle chiuse e limitate sono dei Compatti.
°°°°°°°°

Seguirà …
Lo studio…Limiti in uno Spazio Metrico…
Tag: funzioni continue, Funzioni continue in uno Spazio Metrico
 uno spazio metrico
uno spazio metrico  uno spazio metrico
uno spazio metrico 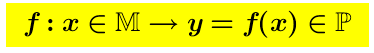 Sia a ∈ M un punto fisso non isolato (IV.15.a).
Sia a ∈ M un punto fisso non isolato (IV.15.a).  escluso il punto a .-
escluso il punto a .- Il punto x=a si chiama punto di continuità della funzione
Il punto x=a si chiama punto di continuità della funzione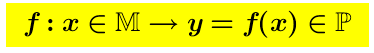 °°°°°
°°°°°
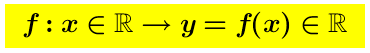


 e
e  Ma poiché questa definizione può essere formulata nei termini di successioni convergenti (V.11.b), la proprietà di una funzione di essere continua in un punto x=a, così come su tutto l’insieme M non é violata sostituendo le metriche degli spazi metrici
Ma poiché questa definizione può essere formulata nei termini di successioni convergenti (V.11.b), la proprietà di una funzione di essere continua in un punto x=a, così come su tutto l’insieme M non é violata sostituendo le metriche degli spazi metrici  e
e  con quelle omomorfe (III.34).
con quelle omomorfe (III.34). come dominio di definizione e
come dominio di definizione e come dominio di valori é fornito da una funzione costante
come dominio di valori é fornito da una funzione costante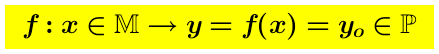 dove
dove  é un punto fisso dello spazio
é un punto fisso dello spazio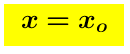 dello spazio
dello spazio  deriva dalla relazione (III.32.b)
deriva dalla relazione (III.32.b)
 .
. in generale non coincide con la palla chiusa
in generale non coincide con la palla chiusa  ma è inclusa strettamente.
ma è inclusa strettamente. appartiene alla sua chiusura se e solo se esiste una successione di elementi di
appartiene alla sua chiusura se e solo se esiste una successione di elementi di  di cui x è il limite.
di cui x è il limite. ma non esistere una successione suddetta.
ma non esistere una successione suddetta. è aderente ad
è aderente ad  se comunque si prenda un intorno dell’elemento
se comunque si prenda un intorno dell’elemento  , l’intersezione dell’intorno con l’insieme
, l’intersezione dell’intorno con l’insieme  è sempre non vuota.
è sempre non vuota. appartenente ad uno spazio topologico
appartenente ad uno spazio topologico  è detto punto di aderenza (o punto di chiusura) per un sottoinsieme
è detto punto di aderenza (o punto di chiusura) per un sottoinsieme  di
di  se ogni aperto contenente
se ogni aperto contenente  interseca
interseca  . In simboli:
. In simboli: si indica la palla di raggio
si indica la palla di raggio  e centro
e centro  .
.
 .
.




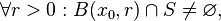
 e
e  (non interessa che
(non interessa che  di
di  diverso da
diverso da 
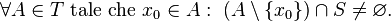

 è la
è la  .
. dei
dei 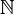 è isolato in
è isolato in  e sia
e sia  un
un 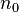 e di raggio
e di raggio 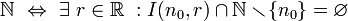 .
. risulta che
risulta che  , deduciamo che
, deduciamo che 

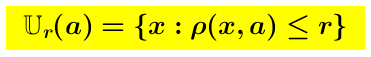




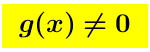

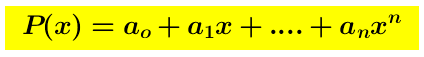
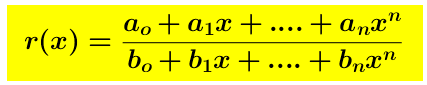
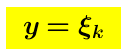

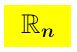




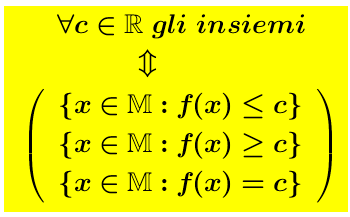





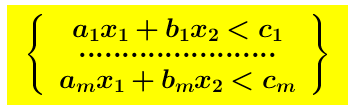
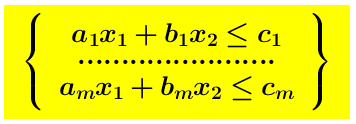


Devi effettuare l'accesso per postare un commento.