“La matematica non conosce razze o confini geografici; per la matematica, il mondo culturale è una singola nazione.”
DAVID HILBERT
°°°°°
Funzioni continue
Definizione :
f è continua in a da destra


°°°°°
Definizione :
f è continua in b da sinistra


°°°°°


°°°°°
La continuità, che è stata definita in un punto, si estende in modo naturale a tutto un intervallo, con la seguente:
Definizione
Siano
I un intervallo
e
f : I → R.
si dice che
f è continua in I se è continua in ogni punto di I
(continua da destra nell’estremo sinistro di I se I è chiuso a sinistra, e continua da sinistra nell’estremo destro di I se I è chiuso a destra).
L’insieme di tutte le funzioni continue in I
(i matematici dicono la classe delle funzioni continue in I)
viene indicata con C(I).
Scrivendo quindi f ∈ C(I) si afferma che la funzione f è continua nell’intervallo I.
°°°°°
Continuità delle funzioni elementari
Si pone ora il problema se quelle che abbiamo chiamato funzioni elementari, e ricordo che si tratta delle potenze, delle esponenziali e delle logaritmiche, che sono tra le funzioni più importanti e più utilizzate in concreto, abbiano la proprietà ora definita, cioè siano continue.
In base a quanto già visto in precedenza non è difficile dare una risposta.
Abbiamo visto che

°°°°°



°°°°°



°°°°°



°°°°°
Si noti che quello che compare a destra nelle tre identità, cioè c^α, b^c, log_b c,
è il valore della funzione nel punto c, cioè f(c).
Questo allora ci dice che:
Proposizione
Le funzioni elementari sono continue nei rispettivi intervalli in cui sono definite.
Può sorgere ora la questione se anche la somma (o la differenza, o il prodotto, o il quoziente) di due o più funzioni elementari sia ancora una funzione continua.
Ricordando
i teoremi dell’algebra dei limiti
(limite di una somma/prodotto/quoziente è somma/prodotto/quoziente dei limiti)
è naturale attendersi che la somma di funzioni continue sia una funzione continua e che lo stesso valga anche con le altre operazioni algebriche.
Vale infatti la seguente
Proposizione
Siano f e g funzioni continue in un certo insieme. Allora f + g, f − g e f*g sono continue in tale insieme; anche f/g, nei punti dell’insieme in cui è definita, è continua.
La precisazione è doverosa dato che il quoziente non è definito dove g si annulla.
°°°°°
Funzioni continue in un intervallo.
Le funzioni continue in un intervallo hanno proprietà globali interessanti, che sono descritte nel teorema seguente.
Teorema (fondamentale delle funzioni continue in un intervallo).
Siano a, b ∈ R e sia f continua nell’intervallo [a, b].
Allora l’insieme dei valori che f assume f([a, b]) è anch’esso un intervallo chiuso e limitato.
Potremmo scrivere quindi che
f([a, b]) è un intervallo chiuso e limitato, ricordando che f([a, b]) indica l’immagine della funzione f,
cioè l’insieme dei valori che essa assume.
Osservazioni :
È importante osservare che se togliamo anche soltanto una delle ipotesi del teorema, la tesi può essere falsa.
È un utile esercizio verificarlo e lo vediamo.
Le ipotesi del teorema sono quattro:
-
che la f sia continua,
-
che la f sia definita in un intervallo,
-
che tale intervallo sia chiuso
-
che tale intervallo sia limitato.
-
Rimuoviamo la prima ipotesi e consideriamo ad esempio f : [0, 1] → R definita da


-
Rimuoviamo la seconda ipotesi e consideriamo ad esempio f : [0, 1]∪[2, 3] → R definita da f(x) = x. La funzione è continua nel suo insieme di definizione, tale insieme è chiuso e limitato, ma non è un intervallo. La tesi è falsa dato che l’immagine di f è [0, 1] ∪ [2, 3], che non è appunto un intervallo.


-
Rimuoviamo la terza ipotesi e consideriamo ad esempio f : (0,1] → R definita da f(x) = 1/x. La funzione è continua e l’intervallo in cui è definita è limitato ma non chiuso. La tesi è falsa dato che l’immagine di f è [1, +∞), che non è limitato (lo studente si disegni il grafico della funzione).


-
Rimuoviamo la quarta ipotesi e consideriamo ad esempio f : [1, +∞) → R definita da f (x) = 1/x. La funzione è continua e l’intervallo in cui è definita è chiuso ma non limitato.
La tesi è falsa dato che l’immagine di f è (0, 1], che non è chiuso (lo studente si disegni il grafico della funzione).


°°°°°
Il teorema fondamentale delle funzioni continue in un intervallo
ha come conseguenze alcune proposizioni che spesso vengono formulate come altrettanti teoremi.
Sia f una funzione continua nell’intervallo [a, b]
-
Teorema dei valori intermedi. Se f(a) < y < f(b), cioè se y è un qualunque valore compreso tra f(a) e f(b), allora esiste c ∈ (a, b) tale che f(c) = y.
-
Teorema degli zeri. Se f (a) e f (b) hanno valori di segno opposto (potremmo scrivere f (a) · f (b) < 0), allora esiste c ∈ (a, b) tale che f(c) = 0.
-
Teorema di Weierstrass. Esiste almeno un punto x_M nell’intervallo [a, b] in cui la funzione f assume il suo valore massimo ed esiste almeno un punto x_m in cui f assume il suo valore minimo.
°°°°°
Osservazioni
Tutte e tre le proposizioni hanno come ipotesi fondamentale che la funzione sia definita in un intervallo chiuso e limitato e che sia continua in tale intervallo.
Il teorema dei valori intermedi
dice sostanzialmente che, nelle ipotesi fatte, la funzione assume tutti i valori compresi tra i valori che la funzione assume agli estremi dell’intervallo [a, b].
Il teorema degli zeri
afferma che, nelle ipotesi fatte, se la funzione assume valori di segno opposto agli estremi, allora c’è almeno un punto in cui essa si annulla.
Osservazioni
Il teorema degli zeri è un caso particolare della proprietà dei valori intermedi, dato che, se f(a)·f(b) < 0, allora f(a) < 0 < f(b) e quindi dalla (2.) si ricade nella (1.).
Osservazioni
Possiamo anche qui vedere che, cadendo alcune ipotesi, la tesi può essere falsa.
Lo facciamo con riferimento al teorema di Weierstrass, ma lo studente può provare a farlo con gli altri.
Si diceva che le ipotesi sono quattro:
-
funzione continua,
-
definita in un intervallo,
-
intervallo chiuso
-
intervallo limitato.
In realtà con il teorema di Weierstrass una delle ipotesi può cadere senza conseguenze,
quella che il dominio sia un intervallo.
Si pensi al secondo esempio visto in precedenza sul teorema fondamentale:
il dominio non è un intervallo
(Attenzione che invece con il teorema degli zeri e il teorema dei valori intermedi nessuna delle ipotesi può cadere:
lo studente lo verifichi su qualche esempio.)
ma la tesi di Weierstrass vale, dato che la funzione ha massimo e minimo (max f = 3 (e x_M = 3) e min f = 0 (e x_m = 0)).
Le altre ipotesi invece non possono cadere.
Vediamolo.
-
Funzione non continua: si consideri la funzione f : [0, 1] → R definita da

-
Si ha inf_x∈[0,1] f(x) = 0 e sup_x∈[0,1] f(x) = 2, ma non esiste né il massimo né il minimo della funzione f e di conseguenza non esiste né x_M né x_m.

-
Intervallo non chiuso:
si consideri la funzione f : (0,1) → R definita da f(x) = x. Si ha inf f = 0 e sup f = 1, ma come prima non esiste né il massimo né il minimo della funzione f.


-
Intervallo non limitato:
il contro esempio più semplice è certamente dato dalla funzione f : R → R definita da f(x) = x. Si ha inf f = −∞ e sup f = +∞, e non esiste né il massimo né il minimo della funzione f.


-
Può destare qualche perplessità la presenza degli infiniti.
Si possono trovare controesempi in cui gli estremi della funzione sono entrambi finiti, come per la funzione


Come la figura suggerisce abbiamo inf f = −1 e sup f = 1, ma non esiste né il massimo né il minimo della funzione f.
°°°°°
Osservazioni
Se nel teorema degli zeri o in quello dei valori intermedi aggiungiamo tra le ipotesi che la f sia crescente o decrescente, possiamo dire che il punto c di cui parla la tesi è unico.
Ci sono interessanti conseguenze dei teoremi appena visti:


In generale:
è garantita l’esistenza di almeno un punto in cui le funzioni assumono lo stesso valore.


L’esistenza di almeno un punto si può dimostrare facilmente, come conseguenza del teorema degli zeri,
ragionando sulla differenza delle due funzioni, cioè su f − g.


Le figure suggeriscono che un’ipotesi che garantisce l’unicità del punto in questione è la monotonia (si osservi che nella figura a sinistra f è crescente e g è decrescente).
Il teorema degli zeri considera il caso di un intervallo chiuso e limitato.
Però può essere facilmente generalizzato ad intervalli che siano non chiusi o non limitati, considerando, anziché il valore della funzione agli estremi, i limiti di questa.
Quindi potremmo riformulare il teorema dicendo che,
se una funzione è continua in un certo intervallo e se i limiti agli estremi hanno segno opposto, allora esiste un qualche punto nell’intervallo in cui la funzione si annulla.
-
Qui a fianco è raffigurato il caso di una funzione f continua nell’intervallo [a, +∞), con



-
Anche il risultato con le due funzioni può essere quindi esteso a tali situazioni più generali. Pertanto ad esempio nel caso siano f, g continue nell’intervallo (a, b), con


allora esiste c ∈ (a, b) tale che :
f(c)=g(c)
-
Se con le due funzioni si assume che f sia crescente e che g sia decrescente, il punto c è unico, cioè l’equazione
f(x) = g(x)
ha una e una sola soluzione in (a, b).
°°°°°
A titolo di esempio,
vediamo come può essere utilizzato tutto questo nella soluzione di un’equazione.
Lo studente ha già visto svariati esempi di equazioni e ha imparato a risolvere classi particolari di equazioni, come le intere di primo e secondo grado, intere di grado maggiore del secondo (a patto di riuscire a fattorizzare il polinomio), razionali, irrazionali, esponenziali, logaritmiche.
Ha anche già visto però che non esistono metodi generali per risolvere una qualunque equazione.
Davanti alla “semplice” equazione x + ln x = 0,
i metodi imparati non servono, dato che l’equazione non rientra nei tipi studiati.
In realtà non esiste un metodo esatto per risolvere tale equazione.
Soltanto con metodi numerici approssimati è possibile trovare una soluzione, cioè un numero razionale “non troppo lontano” dalla soluzione esatta.
In generale è già tanto riuscire a sapere se una data equazione ha almeno una soluzione.
f(c) = g(c).
Grazie alle conseguenze del teorema fondamentale delle funzioni continue in un intervallo è però spesso possibile dire molto, come ora vediamo proprio sull’equazione proposta.
Scriviamo l’equazione come
ln x= −x e poniamo f(x)=ln x e g(x)=−x.
f (x) g(x) Consideriamo le due funzioni nell’intervallo (0, +∞). Si ha


Per quanto visto sopra possiamo dire che esiste almeno una soluzione dell’equazione data nell’intervallo (0, +∞).
Osservando inoltre che
f è crescente e che g è decrescente, possiamo affermare che la soluzione è unica.
Ripetendo le considerazioni precedenti nell’intervallo (0, 1), si può dire che la soluzione è appunto compresa tra 0 e 1, come la figura suggerisce. La soluzione però non si può trovare in modo esatto.

Soluzione:




Soluzione:






°°°°°































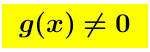











Devi effettuare l'accesso per postare un commento.