iMathematica

Funzioni reali di variabile reale

7.07.- Studio di funzioni reali.-

06.- STUDIO DEL COMPORTAMENTO DELLA FUNZIONE AGLI ESTREMI DEL DOMINIO.-

Lo studio del dominio di una funzione porta a definire gli intervalli di retta reale (asse x) ove esiste la funzione (il valore di y); tali intervalli avranno per estremi o un punto o l’infinito. Se tali estremi non sono punti già studiati come discontinuità, occorre capire il comportamento della funzione “VICINO” a questi punti. Lo strumento idoneo è ancora l’avvicinamento indefinito, ossia il limite.

Occorre conoscere l’andamento della funzione (del valore di y) quando x assume valori prossimi agli estremi del dominio (vicini a piacere); se il dominio ha per estremi −∞ e/o +∞ si indaga per valori di x grandi a piacere (negativi o positivi) e si possono trovare andamenti “infiniti” o andamenti asintotici a rette (asintoti orizzontali o asintoti obliqui).

1. ESTREMO DEL DOMINIO FINITO

Supponiamo che la funzione y = f(x) sia definita in un intervallo aperto ]a , b[ . Allora si deve calcolare il valore della funzione (di y=f(x) ) per valori sempre più vicini ad a (ma più grandi di a) ed il valore della funzione per valori sempre più vicini a b (ma più piccoli di b) .

Si hanno due possibili situazioni:

Caso A)

Se risulta che :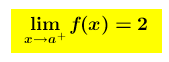allora la funzione si accosta indefinitamente al punto Y2 di coordinate (a , 2) senza comprenderlo

 se risulta che :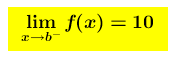allora la funzione si accosta indefinitamente al punto di coordinate (b , 10) senza comprenderlo

Nella figura, la funzione si accosta ai punti “da sotto” ma nulla vieta che si accosti “da sopra”

Caso B)

Se risulta che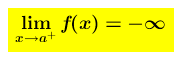allora si ha una situazione perfettamente analoga alla discontinuità di tipo infinito e la retta x = a è un asintoto verticale per la funzione.
Se risulta che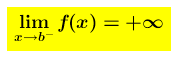allora si ha una situazione perfettamente analoga alla discontinuità di tipo infinito e la retta x = b è un asintoto verticale per la funzione.

figura

Nella figura, il primo infinito ha segno negativo ed il secondo segno positivo, ma potrebbero essere diversi

Osservazione 1

Naturalmente, si possono avere situazione miste tra il caso A) ed il caso B).

2. ESTREMO DEL DOMINIO INFINITO

Supponiamo che la funzione y = f(x) sia definita in un intervallo [a , +∞[ oppure in un intervallo ]–∞ , a]Allora si deve calcolare il valore della funzione ( di y=f(x) ) per valori sempre più vicini a +∞ (grandi a piacere!) oppure per valori sempre più vicini a –∞ (piccoli a piacere!).
In questo caso si hanno due possibili situazioni:

Caso A)

se risulta che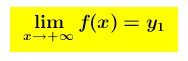allora per valori di x sempre più grandi la funzione (y=f(x)) si avvicina al valore y1 ed il suo grafico si accosta alla y1 retta y = y1 che viene detta asintoto orizzontale della funzione (si dice anche che la funzione è asintotica alla retta)

se risulta che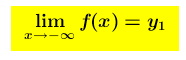

allora per valori di x sempre più grandi la funzione (y=f(x)) si avvicina al valore y1 ed il suo grafico si accosta alla y1 retta y = y1 che viene detta asintoto orizzontale della funzione (si dice anche che la funzione è asintotica alla retta)

figura

Nella figura, la funzione si accosta all’asintoto “da sotto” ma nulla vieta che si accosti “da sopra”

Caso B)

se risulta che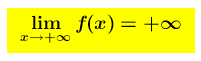
allora per valori di x sempre più grandi la funzione (la y=f(x)) assume valori sempre più grandi ed il suo grafico tende a crescere indefinitamente .

se risulta che

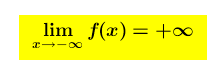allora per valori di x sempre più piccoli la funzione (la y=f(x)) assume valori sempre più grandi ed il suo grafico tende a decrescere indefinitamente .

se risulta che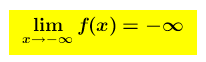

allora per valori di x sempre più piccoli la funzione (la y=f(x)) assume valori sempre più piccoli ed il suo grafico tende a crescere indefinitamente .

se risulta che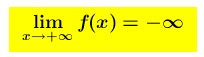

allora per valori di x sempre più grandi la funzione (la y=f(x)) assume valori sempre più piccoli ed il suo grafico tende a decrescere indefinitamente .

Nella figura, i quattro casi possibili:

figura

Esempio

Sia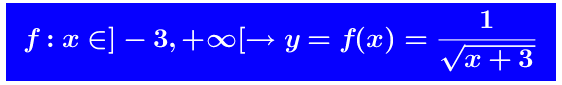il Dominio di f(x) éSi deve studiare il comportamento della funzione agli estremi del dominio, ossia quando x → –3+  e quando x → +∞

Pertanto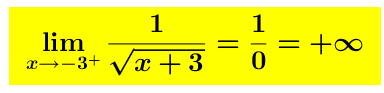

Quindi la retta x = –3 è un asintoto verticale

e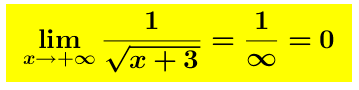Quindi la retta y = 0 è un asintoto orizzontale

Figura

Osservazione

in tutti i casi in cui per x → ±∞ la funzione tende all’infinito (ossia y → ±∞) è lecito chiedersi quale sia la rapidità con cui la funzione diventa infinitamente grande (positiva o negativa che sia). Se la funzione tende all’infinito con la rapidità del primo grado, cioè come una retta, allora significa che per valori di x molto grandi (positivi o negativi) il suo grafico assomiglia ad una retta. Se si conosce l’equazione di questa retta, chiamata asintoto obliquo, allora si deve accostare il grafico della funzione ad essa (solo per i valori di x grandi!)

Figura

°°°°°

Nel caso di una funzione razionale fratta, ossia del tipo Y =N(x)/D(x) , quando X → ±∞ la tendenza della funzione si può determinare attraverso l’analisi del grado di N(X) e D(X).

Più esattamente, si hanno tre casi:

a) se il grado di N(X) è minore del grado di D(X) allora la funzione tende a zero, ossia l’asse x è un asintoto orizzontale per la funzione.

b) se il grado di N(X) è uguale al grado di D(X) allora la funzione tende al numero m/n dove m ed n sono i coefficienti del grado massimo di N(X) e D(X), ossia la retta y = m/n è un asintoto orizzontale per la funzione.

c) se il grado di N(X) è maggiore del grado di D(X) allora la funzione tende a infinito. In questo caso si ha l’asintoto obliquo solo se il grado di N(X) supera di 1 il grado di D(X) e si può determinare la sua equazione eseguendo la divisione tra i due polinomi N(X) e D(X).

Esempio 01

Sia 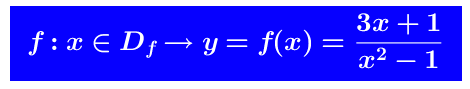il dominio di f(x) é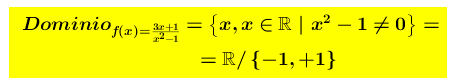poichè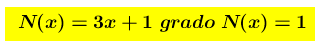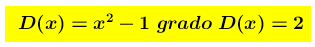si ha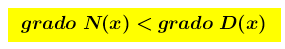

Gli estremi del dominio sono quindi ± ∞ ed ha y senso chiedersi qual è il suo comportamento quando x →± ∞. Poiché è una funzione razionale fratta e siamo nel caso a)

l’asse x è asintoto orizzontale (non si sa se dal di sopra o dal di sotto) figura

Infatti, il calcolo del limite dà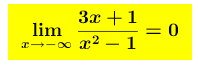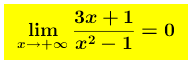Esempio 02

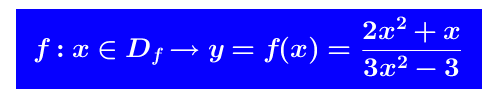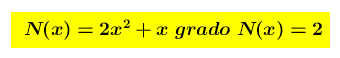
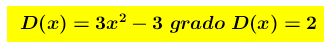
Sia il dominio di f(x) é Gli estremi del dominio sono ±∞ ed ha  senso chiedersi qual è il suo comportamento quando x → ±∞. Poichè 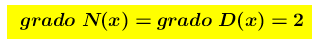è una funzione  razionale fratta e siamo nel caso b)

la retta y= ⅔ è asintoto orizzontale (non si sa se dal di sopra o dal di sotto) Infatti, il calcolo del limite dà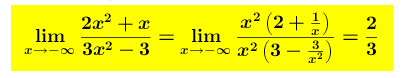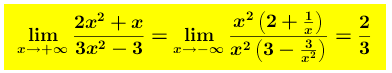Esempio 03

Sia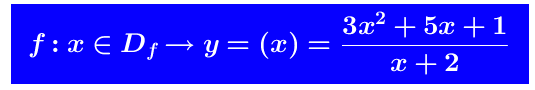il dominio di f(x) é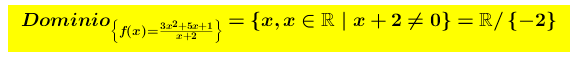

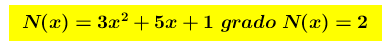
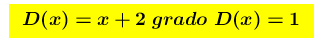
Gli estremi del dominio sono  ± ∞ ed ha senso chiedersi qual è il suo comportamento quando x →± ∞ . Poichè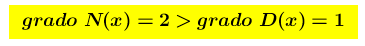è una funzione razionale fratta e siamo nel caso c)

ed è vero che il grado di N(X) supera di uno il grado di D(X) , si è certi che esiste un asintoto obliquo di cui ricercare l’equazione mediante i due noti teoremi (*), oppure con la divisione tra i due polinomi.

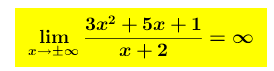
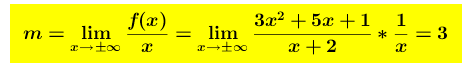
Calcolando i limiti si ha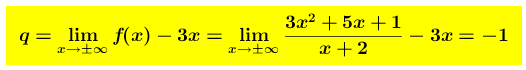La retta ovvero y = 3x – 1 è l’asintoto obliquo ricercato.

figura

Esempio 04

Sia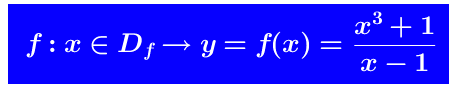il dominio di f(x) é

Gli estremi del dominio sono  ± ∞  ed ha senso chiedersi qual è il suo comportamento quando x → ± ∞. Poiché è una funzione razionale fratta e siamo nel caso c) ma il grado di N(X) supera di due il grado di D(X), la funzione tende all’infinito non come una retta, ma come una parabola (che è di secondo grado!). Con la divisione tra i due polinomi si può   determinare l’equazione della parabola asintotica. Quindi si ha: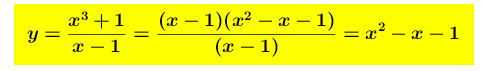

°°°°°°°°°°

 

 

…Seguirà…

… “Studio di una Funzione Reale di Variabile Reale “

Nome(obbligatorio)

E-mail(obbligatorio)

Sito web

Commentare(obbligatorio)

Invia

Δ