
Funzioni reali di variabile reale
7.14.- Studio di funzioni reali.- Esercitazione I
1.- Costruire il grafico della funzione y=f(x) 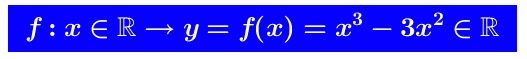 determinando:
determinando:
-
a) Dominio (o Campo di Esistenza)
-
a1) Intersezione con l’ asse x (y=0)e con l’asse y (x=0)
-
b) Punti di discontinuità
-
c) Punti estremali
-
d) intervalli di Crescita e di decrescenza
-
e) Punti di flesso
-
f) Concavità
-
g) Asintoti
°°°°°
Esercizio 01
Sia y=f(x) la funzione razionale intera :
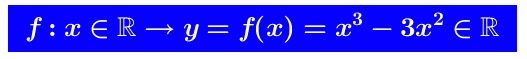 Soluzione:
Soluzione:
a) Dominio di f(x) (o Campo di esistenza) infatti
infatti
a1) Intersezione con gli assi x e y
-
Intersezione asse x – Punti : (O=(0,0) e P=(3,0))

-
Intersezione asse y – Punto : ( O=(0,0) )
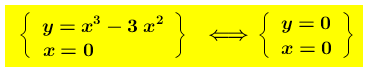
infatti
a2) Simmetrie
Poichè la funzione non é simmetrica.
la funzione non é simmetrica.
a3) Periodicità
Poichè la funzione non é periodica.
la funzione non é periodica.
Quindi:
a4) Segno della funzione
 infatti
infatti
b) Punti di discontinuità
Poichè  grafico
grafico
 la funzione non ha punti di discontinuità.
la funzione non ha punti di discontinuità.
c) Punti estremali
I punti di massimo e minimo assoluto vengono anche detti punti estremali (o estremanti).
Derivata prima e segno relativo
Derivata seconda e segno relativo
-
ricerca massimo e minimo relativo
Calcolo derivata prima
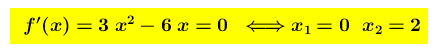 poichè
poichè

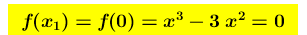 é un massimo relativo
é un massimo relativo
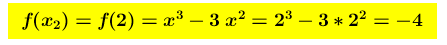 é un minimo relativo
é un minimo relativo
infatti :
-
ricerca massimo e minimo assoluto

d) intervalli di Crescita e di decrescenza
Derivata prima e segno relativo
poichè
 infatti
infatti e) Punti di flesso
e) Punti di flesso
Un punto 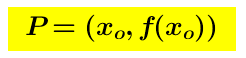 nel quale la concavità del grafico di una funzione passa dalle y positive alle y negative e inversamente si chiama Punto di Flesso.
nel quale la concavità del grafico di una funzione passa dalle y positive alle y negative e inversamente si chiama Punto di Flesso.
Poniamo la derivata seconda uguale a zero 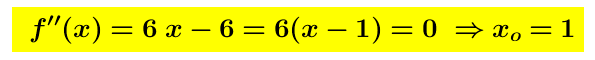 otteniamo così
otteniamo così 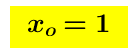 Poichè
Poichè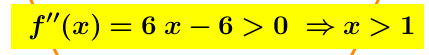 e
e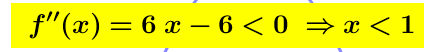 quindi
quindi pertanto
pertanto 

f) Concavità
Nota Bene.:
Si dice che il grafico di una funzione derivabile y=f(x) é Concavo verso il basso nell’intervallo (a,b) se per x ∈ (a,b) l’arco di curva del grafico é situato al di sotto della tangente al grafico della curva tracciata in un punto qualunque dell’intervallo (a,b).
Si dice che il grafico di una funzione derivabile y=f(x) é Concavo verso l’alto nell’intervallo (a,b) se per x ∈ (a,b) l’arco di curva del grafico é situato al di sopra della tangente al grafico della curva tracciata in un punto qualunque dell’intervallo (a,b).
Una Condizione Sufficiente per la concavità verso il basso del grafico di una funzione é che nell’intervallo corrispondente la disuguaglianza f”(x) < 0 sia verificata.
Una Condizione Sufficiente per la concavità verso l’alto del grafico di una funzione é che nell’intervallo corrispondente la disuguaglianza f”(x) >0 sia verificata.
Osservazione 1
Per dire che il grafico di una funzione é concavo verso il basso si dice anche che esso é Convesso verso l’alto.
Per dire che il grafico di una funzione é concavo verso l’alto si dice anche che esso é Convesso verso il basso.
Osservazione  I° Metodo
I° Metodo quindi
quindi
g) Asintoti
Limiti e asintoti
Nota Bene.:
Un asintoto è una retta tale che la distanza tra essa e la curva della funzione y = f (x) tende a 0
per x →∞ (asintoti orizzontali o obliqui) o per x che tende ad un punto ove la f non è definita o è
discontinua (asintoti verticali).
Asintoti Verticali
Si dice che la retta 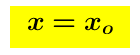 è un asintoto verticale per la funzione y = f (x) se c’è un punto singolare
è un asintoto verticale per la funzione y = f (x) se c’è un punto singolare

(punto di accumulazione escluso dal dominio) in cui si abbia: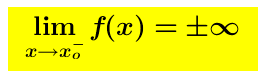 oppure
oppure 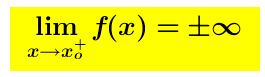
In pratica la curva si accosta sempre più ad una retta di equazione
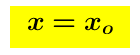 ed è il valore
ed è il valore

(se esiste) ciò che dobbiamo determinare (pertanto una funzione che non abbia punti singolari non può avere asintoti verticali).
Asintoti Orizzontali
Si dice che la retta y = k è un asintoto orizzontale per la funzione y = f (x) se si verifica una delle seguenti condizioni: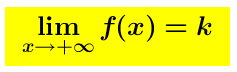 oppure
oppure 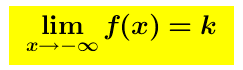
dove k è un numero reale. In pratica la curva si accosta sempre più ad una retta di equazione y=k ed in questo caso è il numero k quel che dobbiamo determinare.
Se si effettua il limite per x tendente verso – ∞si parla di Asintoto Orizzontale Sinistro (A.O.S.), se si effettua il limite per x tendente verso + ∞ si parla di Asintoto Orizzontale Destro (A.O.D.). I due asintoti possono coincidere (A.O.).
Asintoti Obliqui
Se non esiste l’asintoto orizzontale dobbiamo cercare l’eventuale asintoto obliquo (e ciò dobbiamo farlo sia a destra per x tendente verso + ∞ , che a sinistra per per x tendente verso – ∞ ). Una retta si dice asintoto obliquo se il il grafico della funzione si accosta (quando x tende a più o meno infinito) a quello di una retta di equazione y=mx+q (dove m ≠0) , altrimenti si tratterebbe di un asintoto orizzontale). Bisogna quindi determinare i valori m (coefficiente angolare) e q (ordinata all’origine).
Si ha: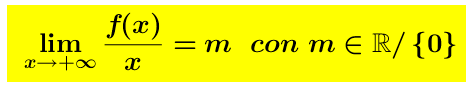 e
e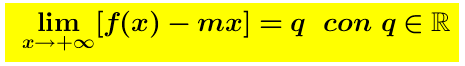
La retta y = mx + q , in tal caso, si dice Asintoto Obliquo Destro (A.Ob.D.).
Analogamentem si ha: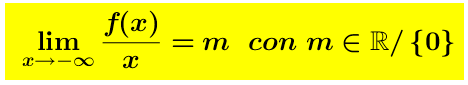 e
e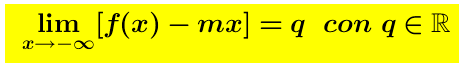 La retta y = mx + q , in tal caso, si dice Asintoto Obliquo Sinistro (A.Ob.S.).
La retta y = mx + q , in tal caso, si dice Asintoto Obliquo Sinistro (A.Ob.S.).
°°°°°
grafico
 ovvero:
ovvero:
°°°°°°°°°°°

…Seguirà…
… Esercitazione… “Studio di una Funzione Reale di Variabile Reale “
Tag: Studio di funzioni reali.- Esercitazione I
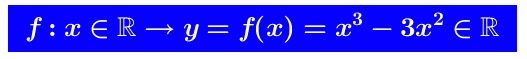 determinando:
determinando: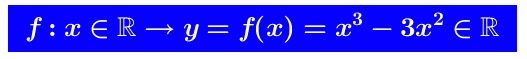 Soluzione:
Soluzione: infatti
infatti


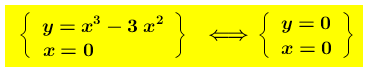









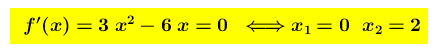
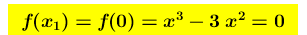
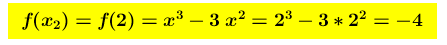




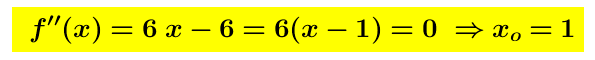
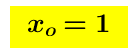
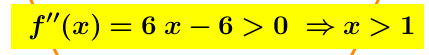
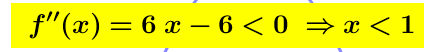






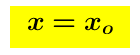

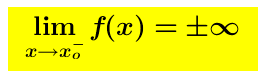
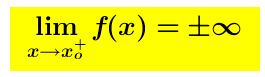
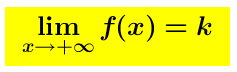
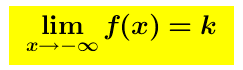
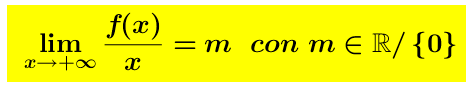
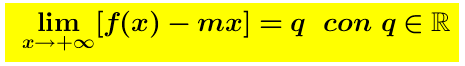
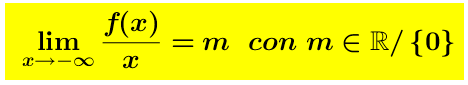
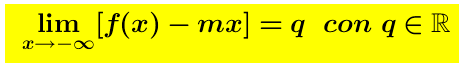



Devi effettuare l'accesso per postare un commento.