iMathematica

Funzioni reali di variabile reale

7.06.- Studio di funzioni reali.-

05.- STUDIO DEGLI EVENTUALI PUNTI DI DISCONTINUITA’ DI UNA FUNZIONE.-

Se vi sono punti di discontinuità per la funzione, occorre determinare il tipo di discontinuità studiando il comportamento della funzione in un intorno (piccolo) di questi punti. Si possono trovare delle discontinuità di tipo “buco” , di tipo “salto” e di tipo “infinito” ; in quest’ultimo caso si ottengono asintoti verticali.

Quando lo studio del dominio indica che la funzione non esiste in qualche punto x_o , occorre studiare l’andamento della funzione VICINO a questo punto. Lo studio si esegue calcolando il limite della funzione quando x tende a quel punto x_o.

Si possono avere tre casi diversi:

A) DISCONTINUITA’ “BUCO” (terza specie)

Definizione 7.6.3.

Data una funzione reale di variabile reale f(x), sia x_o ∈ R un punto di accumulazione del suo dominio; diremo che x_o é un punto di discontinuità di III specie se esiste finito il limite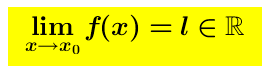ma il valore della funzione in x_o non esiste oppure é diverso da tale limite (f(x_o)∉R oppure f(x_o)≠l ).

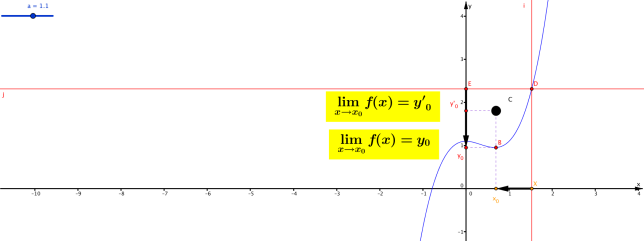
Se dal calcolo del limite risulta che quando x tende a x_o (sia da sinistra che da destra) la funzione tende al valore y_o  allora la funzione manca del punto P(x_0 , y_0) come se vi fosse un “buco” nel grafico in quel punto. 

In linguaggio matematico:

se  x → x_o  allora y→ y_o  (la freccia si legge “tende a”)
lim f(x) = y_o
x → x_o
E’ possibile anche che in x_o la funzione sia definita ma di valore diverso da y_o (il punto nero  figura 1). La discontinuità è eliminabile, basta definire la funzione in quel punto uguale a y_o (e si tappa il buco!).

figura 1

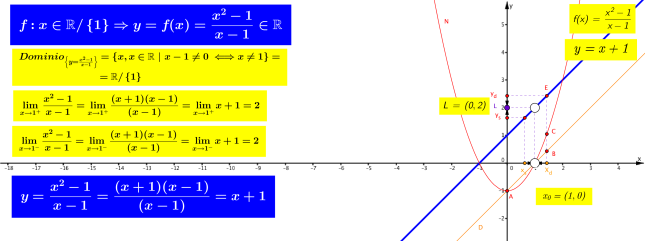
Esempio 1

Sia 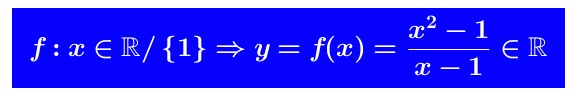la funzione y=f(x) ha per dominioIl punto isolato x = 1 è un punto di discontinuità.

Anche se la certezza si può avere solo mediante il calcolo del limite coi metodi dell’analisi matematica, è evidente che: più x si avvicina al valore 1 (sia da sinistra che da destra) più la funzione ( y=f(x) ) si avvicina al valore 2.

In linguaggio matematico:

Limite destro (limite della funzione y=f(x) per x che tende ad 1 da destra) é uguale a 2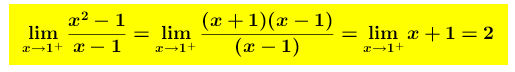Limite sinistro (limite della funzione y=f(x) per x che tende ad 1 da sinistra) é uguale a 2 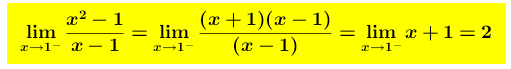Il calcolo del limite suggerisce facilmente il grafico: ricorrendo all’algebra elementare (scomponendo in fattori il numeratore) si ha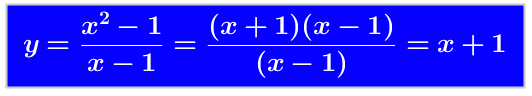che, ad esclusione del valore x = 1, si semplifica e diventa y = x +1 , cioè una retta “col buco”!

grafico 1

°°°°°

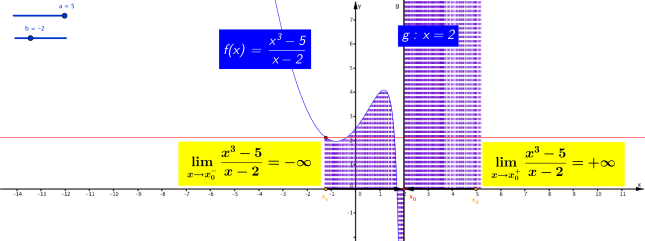
B) DISCONTINUITA’ “INFINITO” (seconda specie)

Definizione 7.6.2.

Data una funzione reale di variabile reale f(x), sia x_o ∈ R un punto di accumulazione del suo dominio; diremo che x_o é un punto di discontinuità di II specie se non esiste o é infinito almeno uno dei seguenti limiti.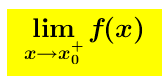e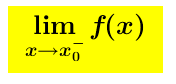Se dal calcolo del limite risulta che quando x tende a x_o (da sinistra o da destra o da entrambe le parti) la funzione tende a ∞ (positivo o negativo che sia), allora il grafico della funzione si accosta sempre più alla retta x = x_o che viene detta asintoto verticale della funzione  (si dice anche che la funzione è asintotica alla retta)

 Si definisce discontinuità di seconda specie anche il caso in cui il limite destro o sinistro o entrambi non esistono.

Nota Bene.:

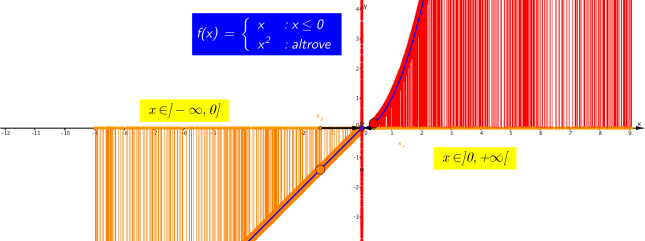
non è detto che una funzione debba avere una formula matematica identica per tutto l’asse reale; si può definire una funzione anche “a tratti”, ossia con espressioni diverse per intervalli adiacenti (come nell’esempio sotto), l’importante è che per ogni valore della x corrisponda un solo valore della y.

°°°°°

C) DISCONTINUITA’ “SALTO” (prima specie)

Definizione 7.6.1.

Data una funzione reale di variabile reale f(x), sia x_o ∈ R un punto di accumulazione del suo dominio; diremo che x_o é un punto di discontinuità di I specie se esistono finiti ma diversi i seguenti limiti.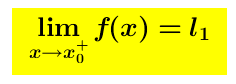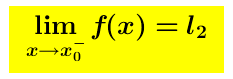In tal caso chiameremo salto della funzione f in x0 la quantita 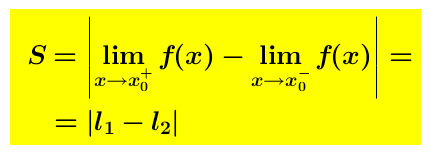Se dal calcolo del limite risulta che quando x tende a x_o la funzione tende da sinistra al valore Y1 e da destra al  valore Y2 (diverso da Y1) allora la funzione ha un grafico spezzato, come se vi fosse un “salto” in quel punto.

In linguaggio matematico :

Limite destro (limite della funzione y=f(x) per x che tende ad 2 da destra) é uguale a 1

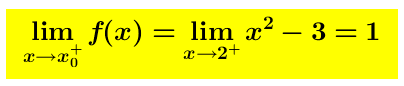Limite sinistro (limite della funzione y=f(x) per x che tende ad 2 da sinistra) é uguale a -2

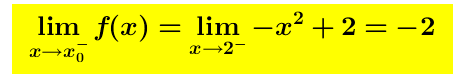La funzione y=f(x) salta dal punto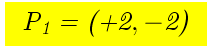al punto  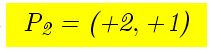come da grafico:

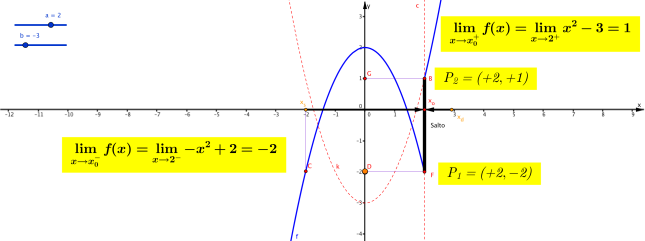Osservazione 1

E’ indifferente che la funzione sia definita o no nel punto x_o , la discontinuità resta e i due punti (x_o ,y_1) e (x_o , y_2) sono i punti di rottura della funzione.

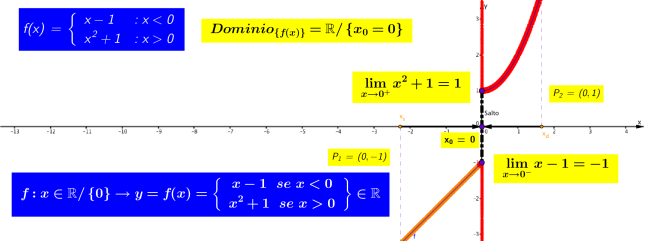
Esempio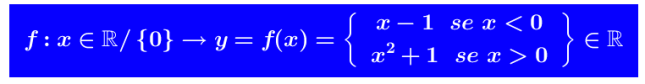Dominio della funzione f(x) é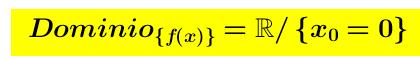quindi

Per il valore X = 0  la funzione non è  definita

A sinistra del valore X = 0 la funzione è definita come una retta (parallela alla bisettrice) e la y assume valori secondo la prima parte della definizione

A destra del valore X = 0  la funzione è definita come una parabola e la y assume valori ricavati dalla seconda parte della definizione.

In linguaggio matematico :

Limite destro (limite della funzione y=f(x) per x che tende ad 0 da destra) é uguale a 1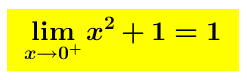Limite sinistro (limite della funzione y=f(x) per x che tende ad 0 da sinistra) é uguale a -1

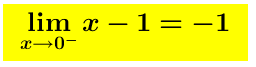La funzione y=f(x) salta dal punto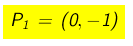al punto  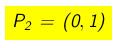come da grafico:

Il segmento di estremi P1=(0,-1) e P2=(0,+1) rappresenta il salto della funzione.

In questo caso la funzione non é definita nel punto x_o , la discontinuità resta e i due punti 

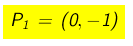e

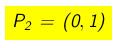sono i punti di rottura della funzione.

Osservazione 2

Da notare che uno di questi due punti potrebbe rientrare nella definizione della funzione ponendo x ≤ 0 oppure x ≥ 0.

°°°°°°°°°°

 

 

…Seguirà…

… “Studio di una Funzione Reale di Variabile Reale “

Nome(obbligatorio)

E-mail(obbligatorio)

Sito web

Commentare(obbligatorio)

Invia

Δ